Géométrie dans l'espace

invited38cc036 · 19/02/2018, 19h19

Bonjour,

Je suis en Terminale S et mon professeur de mathématiques m'a donné quelques exercices pour m'entraîner durant les vacances. Parmi ceux-ci, deux sont sur la géométrie dans l'espace et j'ai vraiment beaucoup de difficultés à comprendre les énoncés.

Exercice 1:
ABCDEFGH est un cube. I et J sont les milieux respectifs de [BC] et [HD]. On nomme K le point d'intersection du plan (AIJ) et de l'arête [CG]. On souhaite construire le plan (P) qui est parallèle au plan (AIJ) et passant par H.
1)En utilisant la section des plans (AIJ) et (P) par le plan (DCG), monterr que le plan (P) coupe le plan (DCG) suivant une droite (delta) qui est parallèle à (JK).
2)Montrer que le plan (P) coupe le plan (ADH) selon une droite (d) parallèle à (JA).
3)Tracer la section du cube par le plan (P). Préciser la nature du polygone obtenu. Justifier.

Exercice 2:
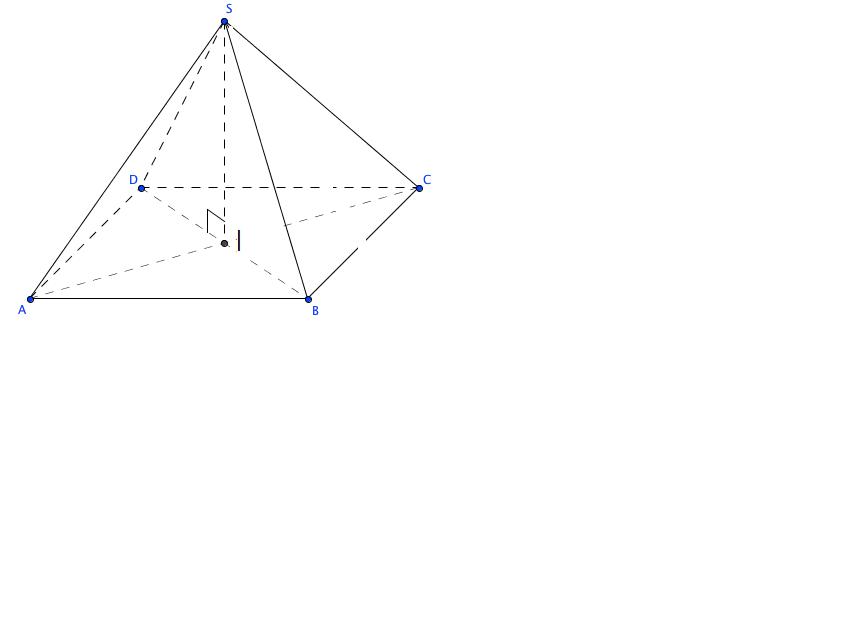
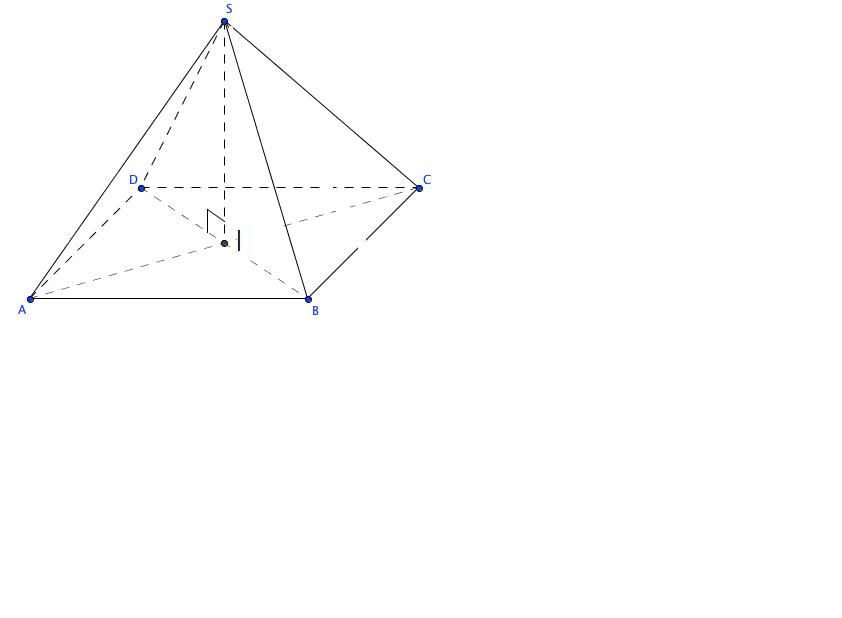
SABCD est une pyramide régulière à base carré. On note I le centre du carré ABCD.
1)Montrer que la droite (AC) est orthogonale aux droites (BD) et (SI).
2)En déduire que les plans (SAC) et (SBD) sont pêrpendiculaires.

Merci de m'apporter un peu d'aide,
Noé

invited38cc036 · 19/02/2018, 19h39

Je vous joins la pyramide de l'exercice 2. Nom : PYRAMIDE exercice 2.jpg
Affichages : 215
Taille : 18,2 Ko

invite51d17075 · 19/02/2018, 19h43

exo1 : question 1)
la question n'est qu'une question de logique ( que l'on peut aisément voir sur un dessin )
K app au plan AIJ et à la droite CG
le plan P est // au plan AIJ et passe par H,
c'est donc le plan // à AIJ "translaté" verticalement de la hauteur JH.
donc ce plan P coupe la droite CG au point K' tel que KK'=JH.
on en déduit que HK' est // à JK.

invited38cc036 · 19/02/2018, 20h07

Merci. Qu'entendez-vous par translaté ?

A voir en vidéo sur Futura · Aujourd'hui

invited38cc036 · 19/02/2018, 20h18

Pour la question 1 de l'exercice 2 :
On a (SI) qui est perpendiculaire au plan (ABC). Par définition, (SI) est orthogonale à toute droite de (ABC), en particulier à (BD) et à (AC).
Dois-je expliquer d'autres choses ?

invite51d17075 · 19/02/2018, 20h20

si je ne trompe pas H est à la verticale de D et J est le milieu de de DH
les plan AJI contient K qui est sur la droite CG
le plan P est // au plan AIJ et passe par H on en deduit
JH=KK' si K' est l'intersection du plan P avec la droite CG ( tout comme K l'est pour le plan AIJ )

invite51d17075 · 19/02/2018, 20h21

je ne répond pas pour l'exercice 2) , pas encore vu la pièce jointe.

invited38cc036 · 19/02/2018, 20h24

La pièce jointe est dans mon deuxième message. Je vous la joins encore une fois. Nom : PYRAMIDE exercice 2.jpg
Affichages : 185
Taille : 18,2 Ko

invite51d17075 · 19/02/2018, 20h25

Envoyé par Nonimamie

Pour la question 1 de l'exercice 2 :
On a (SI) qui est perpendiculaire au plan (ABC). Par définition, (SI) est orthogonale à toute droite de (ABC), en particulier à (BD) et à (AC).
Dois-je expliquer d'autres choses ?

c'est OK, mais tu dois dire aussi pourquoi (AC) est orthogonale à (BD).

invited38cc036 · 19/02/2018, 20h28

Pour la question 2 de l'exercice 2,
On a (SI) qui est inclus dans le plan (SAC) et (SI) qui est inclus dans le plan (SBD). Par définition, le plan (SAC) est perpendiculaire au plan (SBD). Est-ce correct ?

invited38cc036 · 19/02/2018, 20h34

Dois-je expliquer pourquoi (AC) est orthogonale à (BD) ou simplement l'énoncer ?

invite51d17075 · 19/02/2018, 20h35

non, c'est insuffisant une droite peut être incluse dans deux plans distincts sans que ceux ci soient perpendiculaires.
il faut qcq chose de plus.

invited38cc036 · 19/02/2018, 22h28

J'ai utilisé la définition : Deux plans sont perpendiculaires lorsque l'un contient une droite qui est perpendiculaire à l'autre. Que dois-je rajouter pour que ma réponse soit correcte ?

invite51d17075 · 20/02/2018, 01h08

pour (AC) et (BD) , il faut l'expliquer , ça marche parce que la base est carrée.

invite51d17075 · 20/02/2018, 01h12

Envoyé par Nonimamie

J'ai utilisé la définition : Deux plans sont perpendiculaires lorsque l'un contient une droite qui est perpendiculaire à l'autre. Que dois-je rajouter pour que ma réponse soit correcte ?

c'est faux. et pas clair "à l'autre quoi" ?
il faut ( par exemple ) qu'une droite d'un plan soit perpendiculaire à deux droites sécantes du plan. ( pas à une seule autre droite )
car des deux droites sécantes du plan, on peut en tirer un repère.
donc si une droite est perp à deux droites sécantes d'un plan , elle devient perp à toutes les droites du plan.

**gg0** · 20/02/2018, 08h56

Heu ..il faut comprendre "perpendiculaire à l'autre plan"

Mais ce n'est pas ce qu'a utilisé Nonimamie, qui évoque le théorème, mais raconte des choses qui n'ont rien à voir.

Cordialement.

**gg0** · 20/02/2018, 10h47

Nomamie :

Toujours l'exercice 2. Rappel : deux droites perpendiculaires dans un plan de l'espace sont perpendiculaires; deux droites de l'espace sont orthogonales si une parallèle à l'une est perpendiculaire à l'autre (donc dans un même plan). Une droite est perpendiculaire à un plan lorsqu'elle est orthogonale à toutes les droites de ce plan; pour prouver qu'une droite est perpendiculaire à un plan, il suffit de prouver qu'elle est orthogonale à deux droites sécantes de ce plan.

Donc il t'est facile de justifier que (AC) est perpendiculaire à (BD) (voir dans le plan du carré), donc orthogonale à (BD), et comme (SI) est perpendiculaire au plan, de finir la question 1.

Pour la question 2, la définition suffit, mais à condition de t'en servir : Quelle droite de l'un des plans est perpendiculaire à l'autre, et pourquoi (utiliser la question 1) ?

Cordialement.

**gg0** · 20/02/2018, 11h05

Finalement,

je perds mon temps, elle a eu ses réponses sur un autre forum !

invited38cc036 · 20/02/2018, 18h53

Je ne comprends vraiment pas la deuxième question de l'exercice 1.

invite51d17075 · 20/02/2018, 19h00

En quelle classe es tu ?
parce qu'on peut de manière très directe expliquer cela avec les vecteurs.

invited38cc036 · 20/02/2018, 21h47

Je suis en Terminale mais nous n'avons pas encore fait le chapitre géométrie avec vecteurs. Nous avons simplement commencer le chapitre de géométrie dans l'espace ...

invite51d17075 · 21/02/2018, 15h32

reprenons autrement:

ABCDEFGH est un cube. I et J sont les milieux respectifs de [BC] et [HD]. On nomme K le point d'intersection du plan (AIJ) et de l'arête [CG]. On souhaite construire le plan (P) qui est parallèle au plan (AIJ) et passant par H.

1)En utilisant la section des plans (AIJ) et (P) par le plan (DCG), monterr que le plan (P) coupe le plan (DCG) suivant une droite (delta) qui est parallèle à (JK).
2)Montrer que le plan (P) coupe le plan (ADH) selon une droite (d) parallèle à (JA).

Soit deux plans // et un troisième qui coupe ces deux plans.
Comme les deux premiers sont // , les droites ( intersections du 3 ème plan avec ceux ci ) sont elles aussi //
c'est le cas ici
(P) est // à (AIJ)
le troisième plan est le plan (ADH)
l'intersection de (AIJ) et de (ADH) est la droite (AJ)
donc l'intersection de (P) ( parallèle à (AIJ) ) coupe (ADH) selon une droite // à (AJ)

On peut faire exactement le même raisonnement pour la première question ( ce qui évite de parler de translation )

invited38cc036 · 21/02/2018, 22h36

Voilà ce que je propose pur la question 1 de l'exercice 1 :
1)K appartient au plan (AIJ) et passe par H. H est à la verticale de D et J est le milieu de (DH). Le plan (AIJ) contient K, qui est sur la droite (CG). Le plan P est parallèle au plan (AIJ) et passe par H. On en déduit que JH = KK' si K' est l'intersection du plan P avec la droite (CG), comme K l'est pour le plan (AIJ).
Pourriez-vous corriger mes erreurs, s'il-vous-plait ?

2)J'ai la propriété suivante : Si un plan (P) contient deux droites sécantes qui sont parallèles à un plan (P') alors (P) et (P') sont parallèles. Dois-je utiliser cette propriété ?

Merci d'avance pour votre aide.

invite51d17075 · 22/02/2018, 08h39

Envoyé par Nonimamie

Voilà ce que je propose pur la question 1 de l'exercice 1 :
1)K appartient au plan (AIJ) et passe par H. H est à la verticale de D et J est le milieu de (DH). Le plan (AIJ) contient K, qui est sur la droite (CG). Le plan P est parallèle au plan (AIJ) et passe par H. On en déduit que JH = KK' si K' est l'intersection du plan P avec la droite (CG), comme K l'est pour le plan (AIJ).
Pourriez-vous corriger mes erreurs, s'il-vous-plait ?
.

ce que j'ai mis en gras est faux.
ensuite quand tu écris

JH = KK'

, c'est peu clair. Ou bien tu dis que les droites sont les même et c'est insuffisant , ou bien que les distances ou normes des vecteurs sont les mêmes.
|JH|=|KK'|
c'était le sens de ma première proposition avec mon approche sur la "translation" du plan (AIJ) en plan (P)
mais je trouve ma seconde proposition plus simple.
un plan sécant à deux plans // coupe ceux ci en deux droites qui sont aussi //
car cette propriété ( si tu l'as vue ) permet de répondre aux deux questions.

je ne comprend pas comment tu penses utiliser la propriété que tu mentionnes ensuite.

invited38cc036 · 22/02/2018, 09h26

Voilà ce que je propose pour la question 1 de l'exercice 1.

1) K appartient au plan (AIJ) et passe par H. H est à la verticale de D et J est le milieu de (DH). Le plan (AIJ) contient K, qui est sur la droite (CG). Le plan P est parallèle au plan (AIJ) et passe par H. On en déduit que JH = KK' si K' est l'intersection du plan P avec la droite (CG), comme K l'est pour le plan (AIJ).
Pourriez-vous corriger mes erreurs, s'il vous plaît ?

2) J'ai la propriété suivante. Si un plan (P) contient deux droites sécantes qui sont parallèles à un plan (P') alors (P) et (P') sont parallèles. Dois-je utiliser cette propriété ?

Merci d'avance pour votre aide.

invited38cc036 · 22/02/2018, 09h35

Désolée pour ma réponse précédente, c'est une erreur ...

Pour la question 1 exercice 1, je pense également que c'est plus simple avec cette deuxième propriété mais je ne suis pas sûre des plans à utiliser.
1) On a (ABF) et (DCG) qui sont parallèles puisque ABCDEFGH est un cube et (JK) est incluse dans (DCG).
Donc (JK) // (ABF). Mais je crois que je ne réponds pas à la question ...

invite51d17075 · 22/02/2018, 09h40

Envoyé par Nonimamie

Mais je crois que je ne réponds pas à la question ...

ben non, justement.
et la propriété que tu évoques permet de déduire des parallélisme de plans, ici on cherche à déduire des parallélisme de droites à partir de ceux des plans

invite51d17075 · 22/02/2018, 09h45

le plus simple est ( pour la 1) par exemple de dire que si K' est ( à l'instar de K ) l'intersection de (P) avec la droite (CG)
alors la droite (HK') app au plan (P)
la droite (JK) app au plan (AIJ)
ces deux plans étant // , les droites aussi, car elle appartiennent au même plan (DCG)

on peut faire le même raisonnement pour la 2)

invited38cc036 · 22/02/2018, 09h55

D'accord, merci, j'ai compris.
Pour la deuxième,
Si K' est l'intersection de (P) avec la droite (AE)
alors la droite (HK') app au plan (P)
La droite (JA) appartient au plan (AIJ). Puisque ces deux plans sont parallèles, les droites le sont aussi car elles appartiennent au plan (ADH).

invite51d17075 · 22/02/2018, 11h26

un bon résumé ici des droites et plans.
la propriété que l'on utilise ici est la propriété 15) du pdf:
http://pierrelux.net/documents/cours/2/espace.pdf

Géométrie dans l'espace