Bonjour,
Voici un exercice de math que j'ai trouvé dans mon livre dans le chapitre "second degré, équations et inequations"
Concernant la première partie de la question je l'ai prouvé en calculant le delta du dénominateur qui était inférieur à 0 et donc il n'y a pas de valeur interdite. En revanche pour la suite je ne sais pas comment faire.
Je rappelle que je suis en 1ère S et qu'on devrait donc pouvoir trouver une solution avec des notions de mon niveau.
Merci d'avance
-----



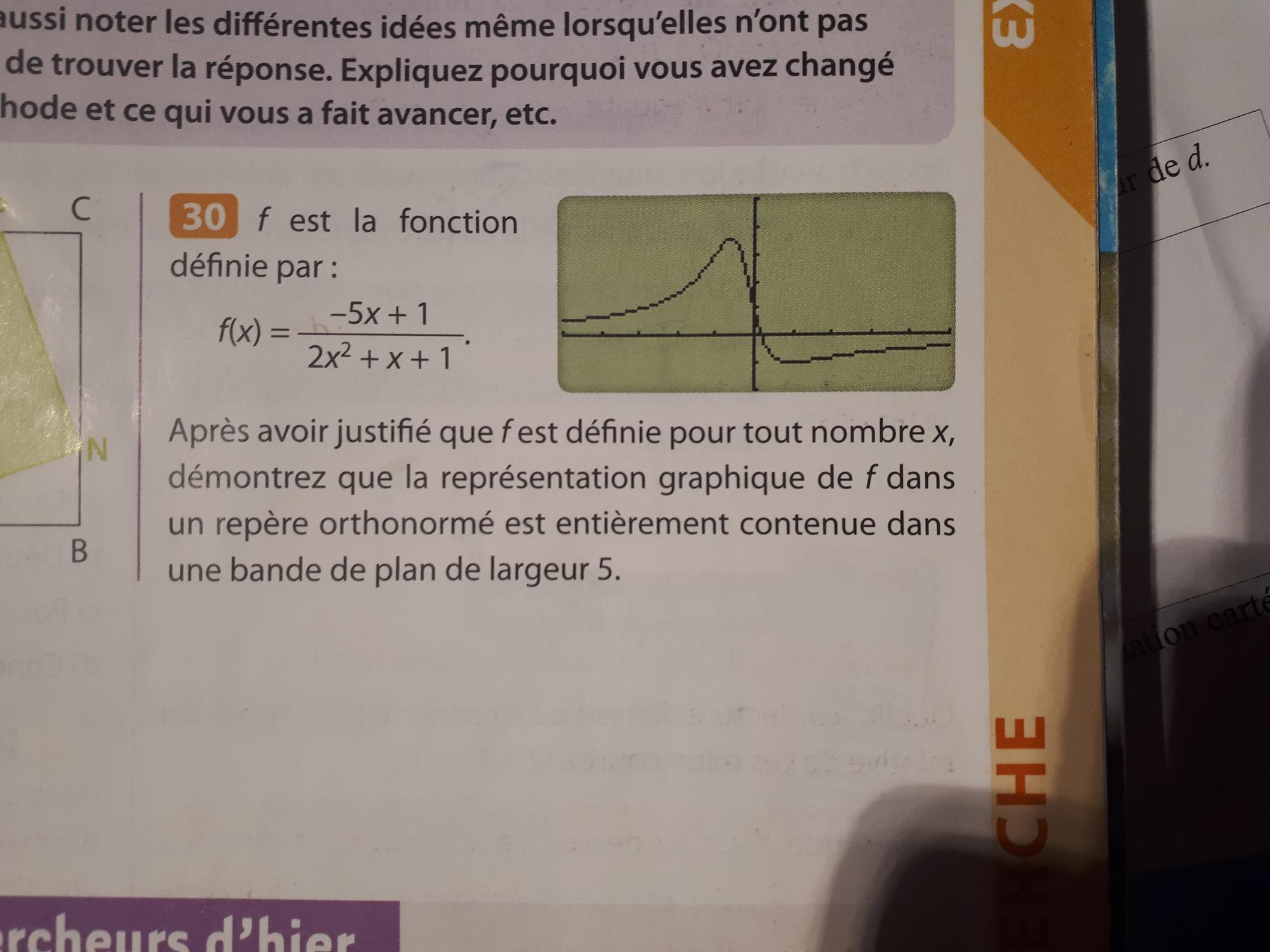
 et
et 
