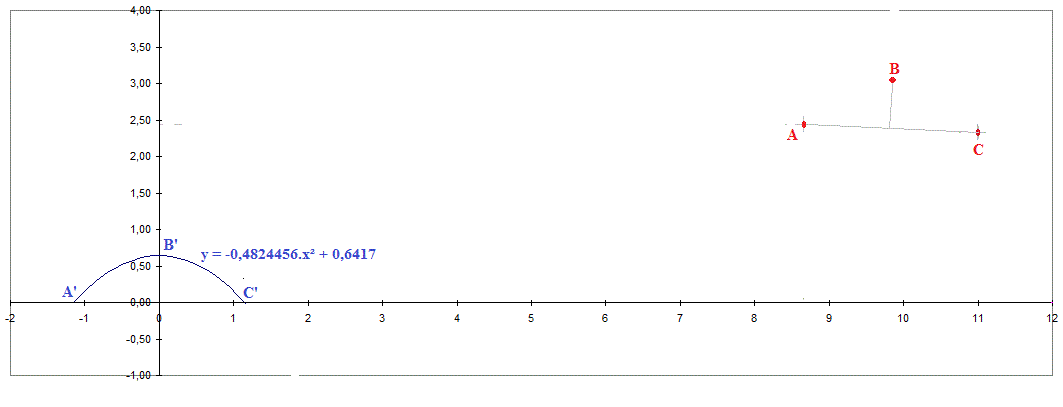
au départ je n'ai vu qu'un y "choisi".Envoyé par Black Jack 2
du fait je ne sais plus quelles sont les figures "imposées".
la pente en A doit elle être // à AB ?
et idem pour la pente en C par rapport à BC. ?
le y(S) est il imposé ? , ou bien doit on trouver une courbe en fct d'un y choisi qcq ?
le point S doit il ( comme le suggère la courbe ) présenter une tangente parallèle à AC ?
plus on rajoute de contraintes, moins on a de chance d'avoir une parabole du second degré.
Merci à toi il faut que je regarde ça à tête reposée bon weekend à tous
Bonjour,
Petite correction à mon message précédent,
Lorsqu'on a la parabole d'équation y = -0,4824456.x² + 0,6417 , pour la ramener dans le repère initial, il faut commencer par la rotation avant de faire la translation et pas le contraire.
Bonjour,
Si tu fais ce que j'ai indiqué dans mes 3 précédents messages, cela correspond à ceci :
La parabole près de l'origine dont j'ai déterminé l'équation, ramenée à le position d'origine ...
C'est à dire déplacer le segment [A'C'] sur le segment [AC] (dont on connait la position), te donne la parabole à axe oblique passant par A, C et le sommet de la pyramide à l'ordonnée 3,015.
Pour le faire mathématiquement, il faut partir de l'équation de la parabole (celle près de l'origine, en bleu) et lui faire subir une rotation et puis une translation.
Bonjour,
...à prendre avec prudence, vu mon niveau...
Il me semble que beber70 travaille dans un repère Oxy et cherche une fonction Y=f(X) définissant les points d'une parabole passant par 3 points (que l'on connaît ou que l'on peut déterminer).
Il semble que, quelle que soit la méthode employée, on arrive à une solution paramétrique...donc trouver X et Y en fonction d'un paramètre P à déterminer, or, beber70 ne peut faire varier que X pour obtenir Y en vue de modifier une trajectoire existante définie dans le repère Oxy (enfin, c'est ce que j'ai compris).
Le cours suivant semble confirmer ce que j'ai dit (même s'il ne traite qu'un cas particulier):
https://www.lapasserelle.com/cours-e...nee/index.html
...mais il est possible que je n'aie rien compris...
Cordialement
Bonjour,
Dans un repère orthonormé Oxy , n'importe quelle conique peut se mettre sous la forme F(x,y) = A.x² + 2B.xy + C.y² + 2D.x + 2E.y + F = 0 (1)
Si on fait ce que j'ai préconisé dans mes deniers messages, soit faire pivoter d'un angle adéquat (celui de la pente de (AC)) et puis une translation de O vers M (point milieu de [AB]) à partir de l'équation y = -0,4824456.x² + 0,6417, on va arriver à l'équation de type (1) de la parabole cherchée dans le repère imposé.
Les valeurs de A, B ... F seront trouvées par les manipulations ci-dessus. C'est un peu calculatoire mais sans vraies difficultés.
Si on préfère avoir une présentation du style y = f(x), elle pourra être obtenue en traitant l'équation (1) (avec les A, B ... F connus) comme une équation du second degré en y, on obtiendra 2 équations images de la parabole cherchée.
Ok j'ai pu me débrouiller avec tout ça,
en résumé:
calcul du point M milieu de AC
calcul du x du point S connaissant le y imposé en utilisant coef directeur droite AC * coef directeur droite MS = -1 (AC perpendiculaire MS)
calcul de l'angle@ entre la droite AC et l'horizontale.
rotation des points A,S de l'angle @ en prenant C comme centre.
calcul de la parabole passant par 3 points A',S'et C
rotation des points de la parabole de l'angle@ pour remettre la droite AC comme à l'origine.
au départ je n'avais pas compris que l'équation d'une parabole passant par 3 points était sur un axe vertical, je pensais naÏvement que la parabole s'orientait en fonction des 3 points d'ou le manque de précision du départ.
Merci particulièrement à BlackJack2 mais aussi à tous ceux qui ont participé à cette discussion et qui m'ont fait progresser.
