Bonjour,
j'ai une machine avec une trajectoire un peu brusque:
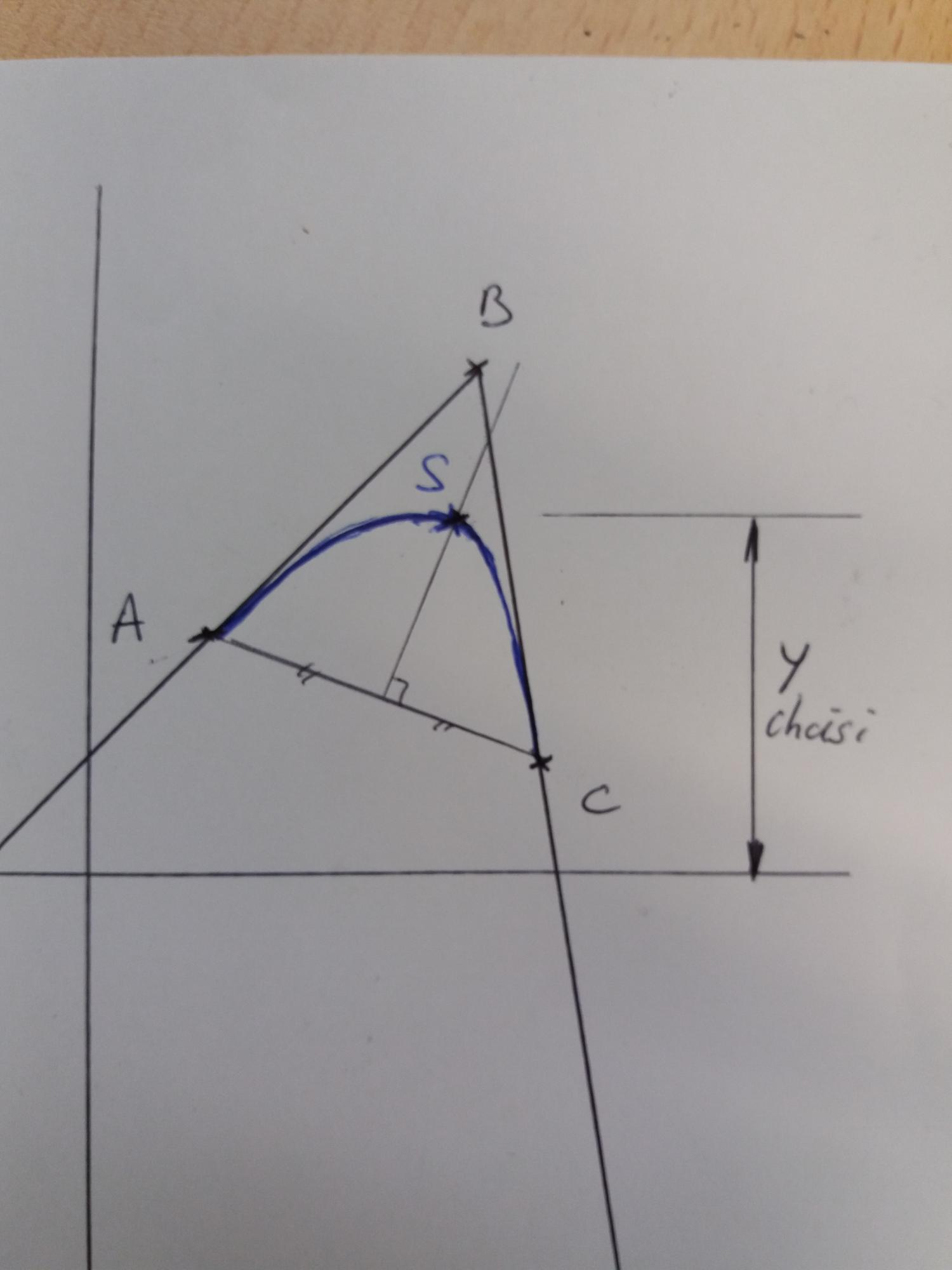
en ligne droite son point de départ A (x=8.7;y=2.456) sont point sommet B (x=10.7;y=3.015) et son point d'arrivée C (x=11;y=2.288).
j'aimerai créer une parabole avec le point de départ A le point d'arrivée C et le point sommet de la parabole S (x=???;y=3.015)
pouvez vous m'aider? mes souvenir de maths de 1ere remontent à 36 ans et je sèche
d'avance merci
Bonjour,
Je suppose que vous n'avez pas besoin de connaitre la méthode de calcul?
Le sommet de la parabole devra se situer à x=9,7746 et l'équation de la courbe sera y=3,015-0,484*(x-9,7746)^2
Why, sometimes I've believed as many as six impossible things before breakfast
Bonjour et merci,
si le calcul m'interresse, en fait les points ne sont jamais les mêmes et je souhaite mettre le calcul dans un tableur pour piloter cette machine à commande numérique.
Bonjour,
L'équation d'une parabole (avec axe // à l'axe des ordonnées) est de la forme : y = ax² + bx + c
Elle est donc définie par 3 coefficients (a, b et c).
Il y a donc un soucis, car en imposant 2 points de passage (A et C) et la position du sommet (C), cela conduit à avoir un système de 4 équations à 3 inconnues ... et dans la majorité des cas, il n'y aura pas de solutions.
C'est d'ailleurs ce qu'on voit ici puisque resartus (dont je n'ai pas vérifié les résultats) t'indique que le sommet de la parabole dont il donne l'équation ne passe pas par le point B.
Bonjour BlackJack
ce qui est imposé ce sont les points de départ et d'arrivée et le y du point sommet, sur un schéma cela me semble possible.?
qu'en pensez vous?
Bonjour Beber70.
Pour le problème que tu poses à la fin du message #1, il y a deux réponses possibles, approximativement les courbes d'équations
y=-0.4841170540 x²+9.464062485x-43.23852380
et
y=-0.002083324099x²-0.03200199351x+2.892104145
Il faut noter que dans le deuxième cas, le sommet est loin de l'intervalle [8,7, 10,7].
Comme les calculs sont assez compliqués, et qu'il faut trouver la "bonne parabole", es-tu vraiment sûr que cette transformation d'un polygone en parabole soit la bonne idée ? les paraboles que j'ai faites calculer par un calculateur algébrique sont-elles vraiment utiles ? leurs sommets sont loin de ton point B.
Cordialement.
Bonjour,
Oui, c'est OK dans un tel cas.
A(8;2,456)
C(11;2,288)
Sommet de valeur 3,015
y = ax²+bx+c
Passe par A --> 64.a + 8b + c = 2,456
Passe par C --> 121.a + 11b + c = 2,288
Valeur du sommet : -b²/(4a) + c = 3,015
Il faut donc résoudre le système :
64.a + 8b + c = 2,456 (1)
121.a + 11b + c = 2,288 (2)
-b²/(4a) + c = 3,015 (3)
(2)-(1) --> 57a + 3b = -0,168
b = -0,056 - 19a (4)
(1) - (3) : 64.a + 8b + b²/(4a) = -0,559
avec(4) -->
64.a + 8.(-0,056 - 19a) + (-0,056 - 19a)²/(4a) = -0,559
a = -0,28455
b = 5,35045
c = 2,456 - 64a - 8b = -22,1364
y = -0,28455.x² + 5,35045.x - 22,1364
Mais l'abscisse du sommet (qu'on n'a pas le droit d'imposer) est 5,35045/(2*0,28455) = 9,4016
Bizarre, Black Jack 2, tu ne trouves qu'une seule solution !! Alors que ton a est donné par une équation du second degré.
Cordialement.
Bonjour
Pas si bizarre, en effet :
Il y a une 2eme solution ... qui ne convient pas.
En tenant compte du fait que d'après les données de l'énoncé initial, l'abscisse du sommet est quelque part entre celles des point A et C ... (bien que sa valeur précise ne peut pas être donnée).
En effet :
64.a + 8.(-0,056 - 19a) + (-0,056 - 19a)²/(4a) = -0,559
(64a - 0,448 - 152a).4a + (-0,056 - 19a)² = -2,236.a
-352a² - 1,792.a + 0,003136 + 361a² + 2,128.a = - 2,236.a
9a² + 2,572.a + 0,003136 = 0
a = - 0,28455 ou -0,0012245
Si je considère la solution avec a = -0,0012245, il vient
a = -0,0012245
b = -0,0327339
c = 2,79627
y = -0,0012245.x² - 0,0327339x + 2,79627
Mais l'abscisse du sommet est alors -13,36, soit en dehors de ]8 ; 11[ imposé par les points A et C.
Reste à voir évidemment ce qui est vraiment attendu
Bonsoir Black Jack et gg0
merci de vous pencher sur mon problème.
le point sommet de la parabole S=(x=9.4016;y=3.015) calculé par Black Jack ne me semble pas déconnant et pas si éloigné du point sommet B (x=10.7;y=3.015).
je vais essayé de retranscrire cela dans mon programme pour tester. Je pourrais ainsi diminuer la valeur du y pour aplatir la parabole et rendre le mouvement plus doux.
Concernant la remarque de gg0 est ce qu'il y a une seule parabole qui passe par 1 point de départ et darrivée connus et une ordonnée connue du point sommet ?
encore merci
Non, il y en a deux.
Black Jack 2 le dit bien, il y en a une autre "qui ne convient pas".
le problème est que, si on veut automatiser la recherche des "bonnes paraboles, il faudra en tenir compte. Les formules de calcul sont déjà très délicates à traiter dans un tableur (risque d'erreur de copie), rajouter des conditions sera encore plus pénible. Sans compter qu'il faudra que le sommet soit cohérent avec les deux points.
Cordialement.
@beber;
difficile de savoir ce que tu cherches exactement.
une solution est d'imposer l’abscisse x0 ou il y a un extrema.( la ou la dérivée s'annule )
mais sans imposer f(x0)
avec cette condition , on en revient à 3 équations à 3 inconnues.
Bonjour,
Pas sûr d'avoir otut compris de ce que tu veux faire...Ci-joint, une solution par EXCEL (tendance + solveur) qui confirme des valeurs données plus haut.
Pas sûr que cela te soit utile... mais bon....
Cordialement
Bonjour ansset,
Ton message 12.
Attention quand même à tous les cas particuliers, par exemple :
La parabole passe par A(-3 ; 3) et C(-1 ; 3) et sommet à l'abscisse -2
On risque bien d'avoir un système de 3 équations à 3 inconnues ... qui aboutit à y = -1/3.x² - 4/3.x + 2
Mais, il me semble qu'il y a, dans un tel cas, une infinité d'autres solutions, par exemple :
y = x² + 4x + 6
y = 2x² + 8x + 9
et une infinité d'autres.
pas vérifié tes calculs, mais raison sur le fond.
ex :
f(x)=a(x-1)(x+1)
f(1)=f(-1)=0 et la dérivée s’annule en x=0 pour tout a.
ma suggestion n'est donc pas ad hoc, mais il reste que je ne saisi pas bien le but de le la manip inititiale.
Bonjour à tous,
pour expliquer un peu mieux:
la courbe représente les points d'un axe de rotation de la machine; la machine va dans le sens - j'usqu'au sommet B et repasse en + pour rejoindre le point C.
ce qui se traduit par un brusque changement de sens
en créant une parabole en remplacement de la pointe le mouvement est adouci.
Je vais corriger mon y jusqu'à ce que la machine est une trajectoire douce sans pour autant m'éloigner trop de la trajectoire initiale qui représente la trajectoire parfaite pour réaliser la pièce. Cela passe évidemment par de nombreux essais.
Sauf erreur de ma part, dans le programme de Ansset que je remercie au passage, le point 2 ne passe pas par le sommet de la parabole.
Quand je mets la valeur trouvé par Black Jack 2 dans le programme de Ansset (9.4016) je vois également que ce point ne correspond pas au sommet de la parabole, ce point devrait se trouver sur la bisextrice de la droite AC.
est ce la même équation que Black Jack2?
cordialement
je parlais du programme excel de mécano41 et pas Ansset
merci aussi à mécano41
la valeur calculée par RESATRUS 9.7746 semble bonne dans le programme de mécano41
Bonjour,
Suite à un énoncé mal défini, les répondeurs (tous ?) sont partis sur une parabole avec l'axe perpendiculaire à l'axe des ordonnées ...
Ce qui n'est pas le cas avec le dessin du message 16.
Et sur le dessin, le Y choisi correspond-il au sommet de la parabole, ou au point le plus haut ? De plus, la parabole semble tangente aux droites en A et C.
C'est un tout autre problème ....
effectivement,
présenté ainsi, on s'est tous un peu planté sur ta problématique.
si tu connais les positions de A et C, il convient peut être d'effectuer d'abord une rotation pour avoir une parabole orientée verticalement.
sauf que ton dessin ne semble pas présenter une parabole centrée sur le milieu de AC justement
d'ou ?????
Bonjour,
Il me semble que dans le schéma du message #16, la droite perpendiculaire au milieu de AC devrait passer par S et par B...
Bien que mes connaissance en maths soient limitées, j'en étais arrivé à soupçonner une parabole inclinée mais je me posais la même question que gg0 au message #20.
Cordialement
en tout cas, tel que dessinée, ce n'est pas une parabole du second degré ( même inclinée )
Déjà excusez moi car je n'ai pas était assez précis dans mon énoncé,
oui la parabole s'oriente suivant l'inclinaison de la droite AC
le sommet S de la parabole est bien sur la perpendiculaire à AC,la perpendiculaire à AC passe par le milieu de AC.
la parabole ne passe pas par B
pas de tangence obligée aux droite en A et C
Et sur le dessin, le Y choisi correspond-il au sommet de la parabole, ou au point le plus haut ? pour moi au sommet de la parabole.
donc, elle n'est pas du second degré.
pardon, donc, il n'y a plus l'exigence des tangentes symétriques ?
ps: ton dessin ne semble pas du tout à l'échelle car avec les chiffres donnés , l'angle AC est très faible ( env -4° )
ce qui n'apparait pas sur la figure.
Non mon dessin n'est pas à l'echelle.
je ne sais pas ce que c'est les tangentes symétriques
Bonjour,
si S est bien le sommet de la parabole à axe oblique.
A(8,7 ; 2,456)
C(11 ; 2,288)
B( ? ; 3,015)
Soit M le point milieu de [AC] = M(9,85 ; 2,375)
Droite (AC) : y = -0,07304.x + 3,091478
--> La perpendiculaire à (AB) passant par M : y = 13,6911.x - 132,482335
Si ymax = 3,015 --> 3,015 = 13,6911.x - 132,482335
x max = 9,8967
On a donc B(9,8967 ; 3,015)
donc (9.8967;3.015) c'est le point S
et comment construit on la parabole ?
Bonjour,
On peut trouver l'équation de la parabole en ramenant par rotation (AC) // à Ox et ramener le point M à l'origine par une translation.
On calcule |MB| = 0,6417 et |MC| = 1,153286
y = ax² + 0,6417
a * 1,153286² + 0,6417 = 0
a = -0,4824456
y = -0,4824456.x² + 0,6417
Maintenant, il faut ramener cela par une translation et une rotation inverses ...
La translation pour ramener O au point M dont les coordonnée ont été calculées au début (mon précédent message) :
y - 2,375 = -0,4824456.(x - 9,85)² + 0,6417
y = -0,482456.x² + 9,504383.x - 43,792387 (1)
Et puis rotation d'un angle alpha avec tg(alpha) = pente de (AC) : alpha = arctg(-0,07304)
cos(alpha) = 0,997343 et sin(alpha) = -0,0728459
On remplace dans (1) y par Y.cos(alpha) + X.sin(alpha) et x par X.cos(alpha) - Y.sin(alpha)
Et on trouve l'équation (2 parties) de la parabole dans les axes primitifs.
Pas le courage de la faire ... et probabilité non nulle que la rotation soit dans le mauvais sens (à vérifier).
