TPE alvéole abeille

[ansset]

je ne peux pas faire mieux que mon post #49..
tout y est détaillé, sauf le fait que les volumes sont identiques.
mais que tu dis avoir déjà démontré.
-----

[ansset]

tentative de représentation comparative.
le fond hexagonal est en noir.
le fond rhomboïde est en rose/rouge. ( dont ici 1/3 est représenté )
sur le graphique deux segments sont communs. ( ils sont ici en rose )
chaque tiers du fond rhomboïde est donc bien constitué de 1 losange orienté et 2 triangles verticaux.
ces triangles correspondent à une partie ( la moitié en fait ) du fond hexagonal remplacé.
en espérant que ce soit clair.

suis désolé, à chaque fois que j'insère une image directement, elle est aussi rajoutée en pièce jointe.
ce qui fait des doublons involontaires.

cordialement.

[ansset]

et ici la courbe

qui représente la diff entre les deux aires Sr-Sh ( au facteur multiplicatif près ).
on voit clairement l'intervalle où Sr < Sh et où se situe le minima.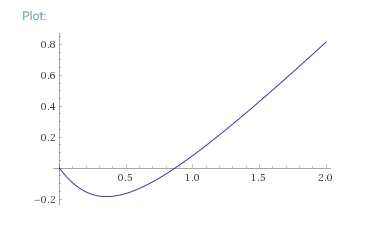

[Paulg75]

Jusqu'ici j'ai compris mais il y'a encore un point flou , si vous me dites que l'aire du prisme à fond rhomboïdale est inférieur au prisme à fond hexagonal cela veut dire qu'il est préférable de construire un prisme a fond hexagonal (promis dernière question )

[ansset]

non justement, si on choisi un bon x, et dans l'idéal celui qui donne l'aire la plus petite ( je ne sais pas ce que font exactement les abeilles : valeur exacte ou approchée ), alors la plus petite surface est la plus économique car qu'on a moins de cire à utiliser, et pour le même volume au final.
de plus, d'un point de vue fonctionnel, cela permet de construire un réservoir plus efficace de part sa forme.
et c'est pourquoi les abeilles font ce choix.

ps : j'ai fait très rapidement mon calcul des 10% , qu'il faudrait vérifier. mais je pense en avoir déjà fait assez, non ?

[ansset]

sur la photo du site wiki avec de vraies alvéoles, il semble qu'on soit très proche du x optimal.

[Paulg75]

Très bien merci beaucoup je pense que là on est bon

[Paulg75]

Cependant j'ai peur de lors de mon oral ne pas mieux l'exprimer comme vous l'avez fait et rendre confus le jury mieux vaut que je fasse comme vous l'aviez dit au début , dériver la fonction ensuite trouver sur quel valeur elle s'annule ?

[ansset]

pour la présentation orale, tu peux résumer la démarche.
- principe de base de la comparaison des deux formes.
- le calcul que tu a fait ( en résumé ) sur l'égalité des volumes
pour les surfaces :
- les dimensions des losanges, triangles, hexagone
sauter les calculs intermédiaires ( en les gardant de coté si on te pose des questions ensuite )
- présenter les résultats définitifs des surfaces
- la fonction simplifiée dont on cherche l'optimal ( donc le minimum )
- sa fonction dérivée.
- les résultats obtenus : l'intervalle ou la solution rhomboïde est meilleure ( entre les deux f(x)=0 ), valeur du x/a optimal.
car si tu prends la fct avec a=1, il faut rappeler à la fin que le x correspond en fait à un x/a .

[Paulg75]

Ah j'oubliais ! Pouvez vous me dire où voyez vous les triangles ? car je n'arrive pas à les visualiser .

Soyons d'accord sur un point surface = aire ? (On ne sait jamais si je me suis trompé)

[Paulg75]

Très bien je vais utiliser cette hiérarchie pour mon oral merci .

J'utilise le même intervalle que j'ai trouvé soit ]0;rac(3)/2[ ?

[ansset]

Ah j'oubliais ! Pouvez vous me dire où voyez vous les triangles ? car je n'arrive pas à les visualiser .

Soyons d'accord sur un point surface = aire ? (On ne sait jamais si je me suis trompé)

bien sûr surface=aire !
les triangles , ben dans la solution rhomboïde (1)
regarde mon schéma post #62, le rhomboïde est constitué de 3*(un losange+2 triangles (2) ).
les triangles sont dans le prolongement de l'hexagone.
si tu ne les mets pas, il resterait des "trous".

(1) tu m'inquiètes là, sur la compréhension de ton exercice !!!!
(2) ce sont, dans le croquis, les triangles ABB1et AFF1 , complémentaires au losange de la figure.

[Paulg75]

En effet je n'ai pas parlé de triangles dans mes calculs c'est pour cela que je questionne mais sinon dans l'ensemble tout est compris !

Mais la rhomboide est constituée de 3 losanges et non de 1 losange et de 2 triangles

[Merlin95]

tentative de représentation comparative.
le fond hexagonal est en noir.
le fond rhomboïde est en rose/rouge. ( dont ici 1/3 est représenté )
sur le graphique deux segments sont communs. ( ils sont ici en rose )
chaque tiers du fond rhomboïde est donc bien constitué de 1 losange orienté et 2 triangles verticaux.
ces triangles correspondent à une partie ( la moitié en fait ) du fond hexagonal remplacé.
en espérant que ce soit clair.

suis désolé, à chaque fois que j'insère une image directement, elle est aussi rajoutée en pièce jointe.
ce qui fait des doublons involontaires.

cordialement.

Je comprends mieux.

Dans cette config, effectivement les volumes des deux structures sont égaux.

[Paulg75]

Ansset impossible que je reprenne vos calculs de post 49 car mon groupe n'a vraiment rien compris et si mon jury leur pose une question à ce propos ils sont foutues ...

Je vais quand même m'inspirer de ce que vous m'avez dit.

Par contre est ce que l'un de vous deux sait comment on peut dériver cette fonction : 2h - x + 1/2*rac(12x^2+3) ?? car j'ai essayé mais dériver cette fonction avec h me pose problème

[ansset]

Mais la rhomboide est constituée de 3 losanges et non de 1 losange et de 2 triangles

comment ça !
tu vois bien qu'il faut les 3 triangles, sinon il y a des trous dans la structure.

Ansset impossible que je reprenne vos calculs de post 49 car mon groupe n'a vraiment rien compris et si mon jury leur pose une question à ce propos ils sont foutues ...

Je vais quand même m'inspirer de ce que vous m'avez dit.

Par contre est ce que l'un de vous deux sait comment on peut dériver cette fonction : 2h - x + 1/2*rac(12x^2+3) ?? car j'ai essayé mais dériver cette fonction avec h me pose problème

concernant la présentation, je pensais que chacun présentait sa partie.
il suffit que l'un comprenne les calculs.

pour le reste :
d'ou vient cette fonction et ce 2h ? d'un post de Merlin ?
et faire intervenir h est très maladroit et "confusionant".

d'autre part, elle ne correspond pas à la différence des surfaces. elle est donc fausse.
et il te sera difficile d'expliquer comment tu l'obtiens.

d'ailleurs elle ne s'annule pas et est tj >0
même si sa dérivée est équivalente ( à un facteur multiplicatif près ) à la dérivée de la bonne fonction.
( h étant cte , la dérivée n'en tient pas compte )

elle donnera donc le bon x optimal, mais avec f(x) >0
difficile de conclure ensuite que la solution "rhomboide" est meilleure.
c'est très casse-gueule d'utiliser cette fonction, qui je le rappelle est fausse !

maintenant, je crois avoir tout expliquer, alors je te laisse relire le fil.

ps : pour la dérivée de ta fonction
(f°g)'(x)=g'(x)f'(g(x))
avec f() fct rac() et g(x)=12x^2+3
tu connais la dérivée de la fonction rac.

[Merlin95]

Attention il te faut bien poser la question, le problème auquel tu t'attaques est différent de celui de ansset.
Ansset considère la comparaison entre deux situations où le volume est le même, cela fait sens car le contenu de l'alveole est une donnée fixe du problème on s'intéresse à la minimisation de la quantité de cire donc de la surface. Quelles sont les aires des deux structures qui offrent un volume constant. La hauteur h n'entre plus en question mais à toi de voir si cette reformulation du problème correspond à ce que tu dois étudier. Si tu poses mal le problème tu risques de ne rien démontrer d'intéressant, voir même de démontrer des résultats qui n'ont pas de sens.

Dans la configuration de ansset il propose que h=x (si j'ai bien compris) de manière que la comparaison soit faite sur des volumes égaux. Dans ton cas, si le h est une constante du problème quand tu vas dériver la fonction la dérivée de h est nulle (dérivation d'une constante).

En gros il te faut bien poser le problème avant de le résoudre il faut faire les choses dans ce sens et non l'inverse.

[Merlin95]

d'ou vient cette fonction et ce 2h ? d'un post de Merlin ?
et faire intervenir h est très maladroit et "confusionant".

d'autre part, elle ne correspond pas à la différence des surfaces. elle est donc fausse.
et il te sera difficile d'expliquer comment tu l'obtiens.

Si tu suis un peu ce que fait Paulg75, et avant de dire que le problème vient de ce que j'ai proposé, tu verras que cette fonction a été proposé par lui et pas par moi, ce au message #37 que tu sembles avoir sauté https://forums.futura-sciences.com/m...ml#post6332641.

Donc le problème ne vient pas de là mais du fait que le problème initial est pas très bien posé et surtout est différent entre la config que tu considères à volume constant et celle de Paulg75 où cette contrainte n'a pas été comprise en tout cas prise en compte.

[ansset]

quand je dit "fausse" , c'est bien à prendre au sens ou elle ne correspond pas à la diff des surfaces.
mais elle est équivalente à la fct à optimiser.
c'est d'ailleurs celle-ci ( sans le terme en h et écrite différemment ) qui est donnée sur le site wiki sans explication vraiment claire.

[Merlin95]

Toujours est-il que ce n'est pas moi qui l'ait proposé, encore une fois, relis mon message tu verras que c'est Paulg75 qui l'a proposé sur la base de vos échanges précédents.

[ansset]

Si tu suis un peu ce que fait Paulg75, et avant de dire que le problème vient de ce que j'ai proposé, tu verras que cette fonction a été proposé par lui et pas par moi, ce au message #37 que tu sembles avoir sauté https://forums.futura-sciences.com/m...ml#post6332641.

Donc le problème ne vient pas de là mais du fait que le problème initial est pas très bien posé et surtout est différent entre la config que tu considères à volume constant et celle de Paulg75 où cette contrainte n'a pas été comprise en tout cas prise en compte.

je n'ai pas dit ça, j'ai posé la question, n'ayant pas relu le fil.

sinon, je ne considère pas moi à volume constant, c'est la config proposée dès le post #1 qui induit un volume constant.
il suffit de voir son schéma où il apparait clairement
-que la config hexagonale fait h de hauteur.
-que la config rhomboide fait h+x de hauteur mais ou la structure qui change va de h-x à h+x.
et c'est la nature des structures et leur positionnement qui induit un volume constant.
il ne s'agit en rien d'une contrainte que j'aurai rajouté moi-même.
d'ailleurs, plus loin dans le fil, Paulg75 dit bien qu'il avait prouvé l'égalité des volumes !!!!!!

si le schéma mis dans le premier post te semble peu compréhensible, il suffit de lire aussi le lien sur les alvéoles d'abeille.
car c'est un TPE, avant d'être un exercice mathématique.

bref, pour moi le schéma initial était très clair, mais moins l'explication de la problématique, qui était peut être mal comprise. Et aussi certainement sur la manière de faire les calculs.

[Paulg75]

Personnellement je trouve que mes calculs sont bons car je trouve bien l'intervalle sur laquelle x est optimal, vous m'affligez un grand stress en me disant que tout est faux

[Paulg75]

Aborder le h dans mes calculs n'est pas confusionant puisque j'utilise la hauteur des deux prismes puisque je veux calculer la surface totale des prismes ( c'est peut-être un peu inutile mais je suis sûr de ne pas me tromper lors de mon oral !)

[Merlin95]

bref, pour moi le schéma initial était très clair, mais moins l'explication de la problématique, qui était peut être mal comprise. Et aussi certainement sur la manière de faire les calculs.

En tout cas toujours est-il que Paulg75 ne semble pas avoir compris et je le comprends le premier schéma n'indique pas selon moi un volume constant.

@Paulg75 à quel message avez vous exprimé que le volume est le même ?

[ansset]

Aborder le h dans mes calculs n'est pas confusionant puisque j'utilise la hauteur des deux prismes puisque je veux calculer la surface totale des prismes ( c'est peut-être un peu inutile mais je suis sûr de ne pas me tromper lors de mon oral !)

mais à quoi correspond ta fonction alors ?

[ansset]

@Paulg75 à quel message avez vous exprimé que le volume est le même ?

ici mess #33

En effet grâce à l'utilisation de la symétrie j'ai pu démontrer que les volumes des deux prismes étaient égaux.

hors, les volumes ne peuvent être égaux qu'avec le schéma que j'ai redessiné.

[ansset]

Edit : pause pour moi, un peu de lassitude à force d'incompréhension de partout !!!

[Merlin95]

je suis désolé, mais le 2h n'a rien à faire là.

Et pourquoi ? A la limite le 2h ne me choque pas mais il faut l'exprimer en fonction de x, ce n'est pas une constante.

Ce n'est pas difficile ca donne h = H +x avec H constant (dans la config d'ansset, il a pris H = 0).

Et cela est à faire autant pour l'aire de la structure héxagonal que pour l'aire de la structure rhomboidale.

Donc en repartant des calculs de Paulg75 qui est bon (sauf erreur de calcul) on trouve :
Afp = 2h + rac(3)/2 = 2H + 2x +rac(3)/2
Afr = 2h -x + 1/2*rac(12x^2+3) = 2H + x + 1/2*rac(12x^2+3)

Il me semble mieux d'un point de vue ludique de partir des calculs de Paulg75 pour dire s'ils sont bons ou pas, plutôt que de donner une solution. Il proposait même de détailler son calcul sur les points délicats pour voir s'il y a une erreur.

J'ai regardé son calcul qui me semble correct dans la méthodologie. Par exemple vous trouvez la même chose pour Afp.

Vous trouvez
Afp = 3rac(3)/2 + 6x
Mais lui ne s'intéresse qu'à un tiers de la structure ce qui est logique car c'est symétrique :
Donc vous trouvez pour un tiers de la structure :
Afp = 3rac(3) + 2x + 2H (ansset a pris H = 0 donc vous trouvez en fait la même chose)

Reste à comparer de la même façon vos deux calculs pour Afr.

@Paulg75 ne vous stressez pas.

[Merlin95]

Correction de la fin de mon message :

[...]
Mais lui ne s'intéresse qu'à un tiers de la structure ce qui est logique car c'est symétrique :
Donc vous trouvez pour un tiers de la structure :
Afp = rac(3)/2 + 2x
et Paulg75
Afp = rac(3)/2 + 2x + 2H (ansset a pris H = 0 donc vous trouvez en fait la même chose)

[...]

[ansset]

@Merlin:
son f(x) doit être ( à un coeff près ) la diff entre les 2 surfaces.
puisse qu'il souhaite la dériver pour obtenir l'extréma.
qu'il en prenne un tiers et/ou qu'il mette un autre facteur en commun importe peu.

mais telle qu'elle est écrite les h n'ont rien à faire là. ( pas dans la différence )
par ailleurs , pour x=0, on a pas f(x)=0 , étrange non ?

enfin sa fonction ne devient pas négative sur le premier intervalle.
difficile donc d'expliquer que la solution rhomboide est meilleur avec des bons x.

et tout ça , même si sa dérivée s'annule au bon endroit.

mais comme il dit en dernier qu'il est sur de lui pour son oral, je me tais.