TPE alvéole abeille

[invite51d17075]

Pourquoi reviens tu sur les calculs ? Vous avez trouvé les mêmes formules, non ?

il semble que non.
car

J'ai calculé l'image du minima de la fonction par l'aire l'alvéole a fond rhomboïdal et je trouve : 2h + rac(2)/2

si le h correspond à celui du post 1 et que l'on calcule le tiers de la surface.
je n'obtiens pas le même résultat......
-----

[inviteb4e1c858]

Bref sinon mon calcul final il tient la route ?

[invite51d17075]

en prenant comme toi l'ensemble d'un tiers de l'alvéole ( a=1), j'ai
Sr=(rac(3)/2)(rac(1+4x²)+x+2(h-x) soit
Sr=(rac(3)/2)(rac(1+4x²)-x+2h
et
Sh=(rac(3)/2)+2h

donc je n'obtiens pas le même résultat pour ton Sr. ( ton 2h+rac(2)/2 )

la question du gain en % par contre dépend des surfaces considérées.

si on prend ta méthode on compare la diff entre un seul fond plat par un fond rhomboide.
dans ce cas le gain en % est supérieur à mon calcul. ( d'env 35% au lieu de mes 10%)
même s'il est le même en valeur absolue.
car j'ai calculé le gain en % des surfaces de deux structures volumiques dont l'une est d'une hauteur x et l'autre 2x.
mon gain est donc inférieur.

si on comparait le gain pour l'ensemble de l'alvéole, il serait fct de h et donc encore même inférieur au mien.

donc, pour ce gain relatif, ta présentation peut être plus "parlante".
à condition de faire les bon calculs.

[inviteb4e1c858]

Non il y'a quiproquo !

Je n'ai pas trouvé cette valeur pour Sr voyons pour Sr j'ai trouvé : 2h - x + 1/2*rac(12x^2 + 3)

[inviteb4e1c858]

je remplace x par le minima (rac(2)/4) dans la surface Sr et je trouve : 2h + rac(2)/2 si je dis pas de bêtise.

On voit donc que Sr est < à Sh

[Merlin95]

Non il y'a quiproquo !

Je n'ai pas trouvé cette valeur pour Sr voyons pour Sr j'ai trouvé : 2h - x + 1/2*rac(12x^2 + 3)

Ben oui et j'avais vérifié ca correspond à ce qu'Ansset a trouvé (voir #91).

[Merlin95]

Te revoilà Merlin,

Bah nous avons trouvé les mêmes résultats mais nous ne sommes pas passés par le même chemin en effet ansset a , il ne faut pas se mentir, des meilleurs conjectures que moi or lui les comprend de a à z et moi je comprend des parties puis d'autres non donc en attendant que je comprenne l'intégralité je termine mes calculs car l'oral est dans une semaine .

Ta démarche me semblait aussi bonne que celle d'Ansset je ne comprends pas pourquoi tu dis que tu ne comprends pas certaines choses dans ce que tu as fait. Qu'est-ce qui t'interroge exactement ?

[invite51d17075]

je remplace x par le minima (rac(2)/4) dans la surface Sr et je trouve : 2h + rac(2)/2 si je dis pas de bêtise.

On voit donc que Sr est < à Sh

tu as raison, erreur de calcul de ma part. j'ai repris trop vite ce calcul de ce trop long fil.
désolé.........

[invite51d17075]

faut comprendre que mon post #49 a plus d'une semaine, et que je ne suis revenu sur cette discussion que par interminence, en reprenant à chaque fois la discussion en cours vite fait ( d'autres discussions en cours).
d'ailleurs , j'ai du faire une erreur dans mes calculs à la fin des Sr et Sh / mon modèle.

pour le reste, on n'a pas travaillé de la même manière.

garde ta méthode , car tu l'a déjà travaillé, et en plus elle fait structurellement apparaitre un meilleur gain en %

[invite51d17075]

Je tente un résumé qui me ramène à l'approche de Paulg.
mon calcul initial sur les deux structures donnaient au départ:

Le fond romboide.
surface totale :


le fond hexagonal :
surface :

en prenant a=1 et 1/3 de la structure.


en ajoutant la partie sous ma structure ( qui est de hauteur h-x)





la diff vaut
soit


la dérivée s'annule bien en soit
qui donne le minimum négatif de la différence.

Et en comparant directement les deux surfaces sans h dans les formules.
soit


soit :


et env

suis sûr que c'est tout clair maintenant, en tout cas pour moi.
Cdt

ps : même plus question de parler de deux calculs différents en fait.
même si je n'ai pas fait le rapport des bonnes surfaces à un moment. mea culpa pour ça.

[inviteb4e1c858]

Oui en effet ansset je trouve aussi 0,8 pour la différence mais j'ai une question pourquoi on multiplie le résultat de la différence par 10 pour obtenir un gain en % de cire ?

Et mon ultime question ( enfin devriez vous dire ) sur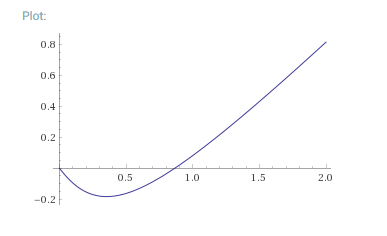

Comment tu peux affirmer que Afr est < à Afp à l'aide du graphique car honnêtement la lecture graphique m'a juste permis de déterminer le minima de la fonction ?

[invite51d17075]

en traçant la courbe de la différence avec wolfram alpha, c'est visible, sinon on peut faire une étude de la fonction.
https://www.wolframalpha.com/input/?...rom+0+to+1%2F2

[inviteb4e1c858]

Non je crois que j'ai mal posé ma question je suis bête...

Enfaite je voulais dire pourquoi dans l'intervalle 0 rac(3)/2 Afr est < à Afp graphiquement ? par ce que on fait Afr - Afp où c'est dû à autre chose ? ( par le calcul je peux le démontrer sans problème mais je préfère tout savoir pour l'oral ).

et dernière question : pourquoi on multiplie le résultat de la différence de Afr par Afp par 10 pour obtenir un gain en % de cire ?

[invite51d17075]

si Arf-Arh <0 alors Arf < Arh !!!!
quand au gain , on fait (Arf-Arh)/Arh soit Arf/Arh -1
qui est un résultat entre 0 et 1 , qui multiplié par 100 donne un %

ps: comme il y a une réduction ce % est négatif, mais c'est un gain. ( comme une remise dans un magasin )

[inviteb4e1c858]

Alors là chapeau ansset et Merlin vous m'avez été d'une grande aide une bonne continuation à vous

[invite51d17075]

erreur dans mon dernier post ( mauvaise écriture de la fonction )
https://www.wolframalpha.com/input/?...-x+from+0+to+2

[invite51d17075]

rappel : le gain calculé (en valeur absolue ou en % ) ne concerne QUE le mode de fermeture, pas du tout le gain ( bien plus faible ) / l'ensemble de l'alvéole.
en revanche tu peux faire un peu de pratique et rapporter cela à une alvéole réelle. ( avec des chiffres ad hoc; c'est un TPE, avant d'être un devoir de maths ).

Et tout laisse à penser que la raison principale de ce choix soit avant tout pour mieux conserver le miel.
d'ailleurs les alvéoles sont aussi inclinées de qcq degrés ( 7à 8 je crois ) pour éviter que cela "coule".

[Merlin95]

l'application numérique du gain à mon avis sera la plus pertinente en se basant sur un volume approximatif conforme à la réalité. Il faudrait bien veiller à garder ce volume constant pour exprimer h en fonction de x (j'ai bien compris que le volume est le même entre les deux configurations par contre quand on fait varier x il faut aussi que h varie afin de conserver le volume constant).

[invite51d17075]

heu, non justement.
enfin question de vocabulaire certainement.
le h de base ne varie pas, et c'est pourquoi le volume est constant.
quand on remplace un haut hexagonal par un haut romboide. ( voir mon croquis #62 ), on enlève un volume sous h que l'on rajoute au dessus. ( des petites pyramides ( 3 au total )de base hexagonale, de hauteur x, et avec un angle droit en un coin )

enfin tout dépend de ce que tu appelle h.
car la hauteur en config romboide est effectivement un peu plus haute , mais plus étroite.
mais on ne fait aucunement intervenir celle ci dans les calculs.

[Merlin95]

Oui en effet c'est juste et erreur de ma part (je parlais bien du h=AD sur le premier dessin).

[inviteb4e1c858]

Afr/Afh = (2h + rac(2)/2) / 2h + rac(3)/2 , ici les 2h s'éliminent donc Afr/Afh = (environ) 0,8 donc il y'a bien un gain de 8% en utilisant un fond rhomboïdal avec une valeur optimal pour x , voilà mon raisonnement ansset avec 1/3 de l'alvéole

[invite51d17075]

Afr/Afh = (2h + rac(2)/2) / 2h + rac(3)/2 , ici les 2h s'éliminent donc .....

je suppose que tu as voulu écrire :
(2h + rac(2)/2) /( 2h + rac(3)/2)
alors non, pas du tout, les 2h ne s'éliminent pas, énorme erreur niveau collège.

et par ailleurs 0,8 correspond à un gain de 20 %
deuxième erreur.

[inviteb4e1c858]

Et du coup il faut pas multiplié par 100 mais par 10 pour le pourcentage

[inviteb4e1c858]

2*h / 2*h = 1 normalement non ??

[invite51d17075]

ce que tu écris est :
(a+b)/(a+c)=b/c , c'est n'importe quoi !!!!

sur ce, tu as tout pour faire ton TPE ( près de 175 mess pour initialement UNE question mathématique )

[inviteb4e1c858]

Mon TPE partie math est achevé mais je voulais mettre un gain en % , il est donc impossible de déterminer ce pourcentage avec mes valeurs ?

[invite51d17075]

tu as un gain en % pour la surface de la "fermeture" uniquement.
pour avoir ce gain sur l'ensemble de l'alvéole, il te faut connaitre le rapport h/a.
( car n'oublies pas, tu as pris a=1 pour simplifier les équations )

ne me demande pas comment faire STP !
c'est TON TPE !

[inviteb4e1c858]

Je ne te demande pas de le faire !!! jusqu'ici je n'ai pris aucun de tes calculs tu m'as accompagné et remis sur la voie en cas d'erreurs (je me demande si tu suis bien ce que je fais parfois ...) il faut savoir faire la différence bref pour h je n'ai pas pris de valeurs justes il n'a que pour a où comme tu t'en est rappelé où j'ai pris 1.



P.S : Je me suis arraché comme un fou pour conclure la partie mathématiques de mes TPE j'ai dû faire des calculs que je n'ai pas vu ailleurs donc me dire " c'est tes TPE !" je trouve ça un peu osé

[invite51d17075]

en te remerciant !

[Merlin95]

Pour l'application numérique il faut que tu cherches sur internet la volume moyen d'une alveole ou la profondeur de l'alvéole ainsi que peut-etre (je ne sais pas si le rapport dépend de a) longueur a du côté de la structure hexagonale.

Tu peux trouver ces indications dans la partie dimension de la fiche Wikipedia :

https://fr.m.wikipedia.org/wiki/Alvéole_d%27abeille