Bonjour, je souhaiterai avoir de l’aide pour l’exercice suivant :
La suite (Un) est définie pour tout entier naturel n non nul, par Un= 1/n(n+1)
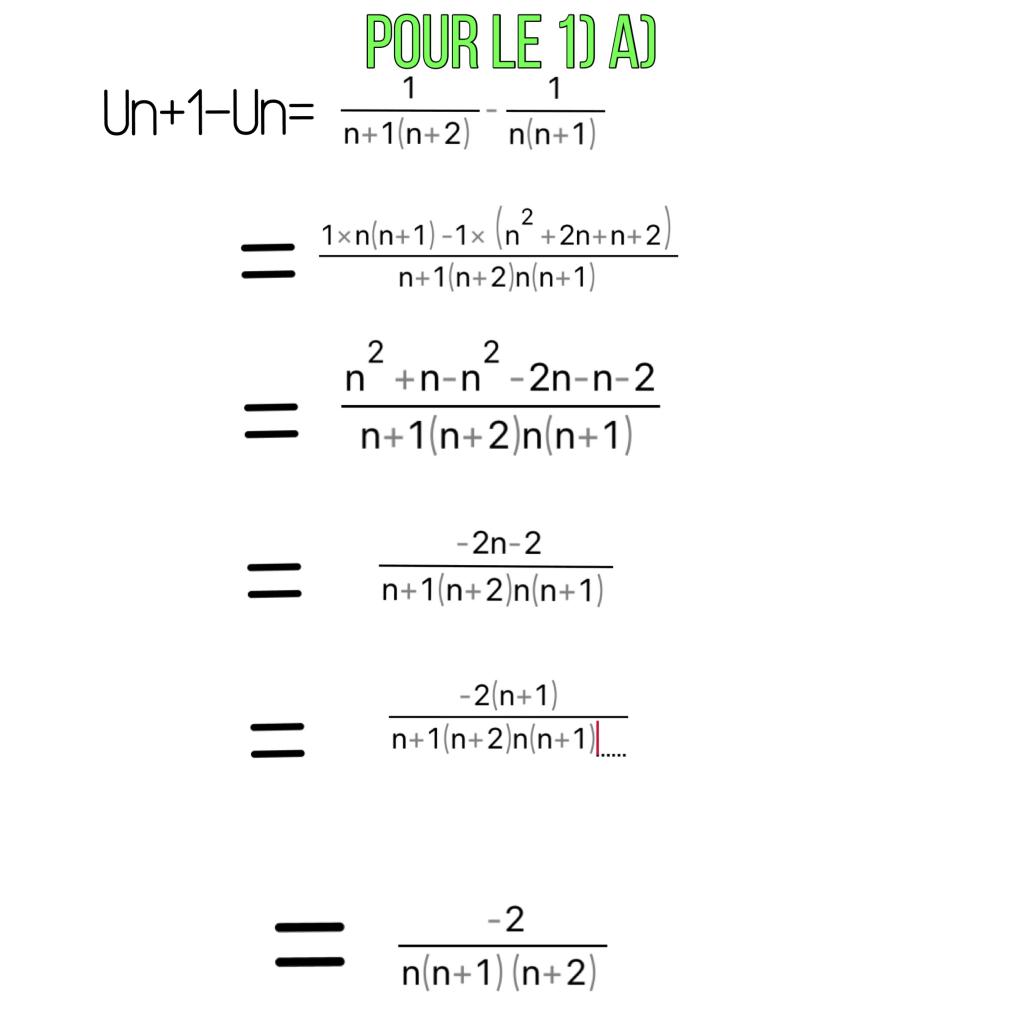
1) a) Montrer que pour tout entier n supérieur ou égal à 1,
Un+1-Un= -2/n(n+1)(n+2)
b) Déterminer le sens de variations de Un
c) À l’aide de la calculatrice, conjecturer la limite éventuelle de Un
2) Pout tout entier tel que p est supérieur ou égal à 1, on a:
Sp=U1+U2+U3+U4+.... +Up
a) Montrer que pour tout entier n supérieur ou égal à 1 que Un=1/n - 1/n+1
b) Montrer que pour tout entier p supérieur ou égal à 1 on a:
Sp=1 - 1/p + 1
c) Calculer 1/2 + 2/2*3 + 1/3*4+....+1/99*100.
d) Conjecturer la limite éventuelle de la suite (Sp)
Mes réponses
1) a) J’ai commencé la démonstration mais je suis bloqué:
Un+1-Un = 1/n+1(n+2) - 1/n(n+1)
=(n2+n)-(n2+2n+n+2)/n+1 (n+2) n(n+1)
Je suis bloqué ici car il y a 2 différentes possibilités pour soustraire chez les numérateurs: •n-2n+n=0
•(2n+n)-n= -2n Je ne sais pas si c’est normal...
b) -2/n*(n+2)*(n+1) > 0 donc cette suite est croissante. Cette réponse suffit ?
c) On a lim 1/n(n+1)=0. Faut-il faire une justification par calcul ?
n—> +oo
2) a) Un= 1/n(n+1) donc:
1/n(n+1) = 1/n2+n = n+1-n/n*(n+1)=
(n+1)*1/(n+1)*n - n*1/n*(n+1) =
(n+1)*1/(n+1)*n - 1/n+1 =
1/n - 1/n+1. C’est correct ?
b) ???
c) Ici 99* 0,5+1/99*100 divisé par 2 = 24,755= 4951/200. Correct ?
d) Ici lim (Sp)=0. Faut-il faire ici une justification par calcul ?
n—>+oo
Merci si vous avez le courage de lire ce pavé et de m’aider ^^
PS: Désolé si les calculs avec les fractions sont très peu clairs, demandez moi si vous voulez que je vous écrive les calculs sur papiers....
-----







 Est-il correct ? Le reste de mes réponses aussi ?
Est-il correct ? Le reste de mes réponses aussi ?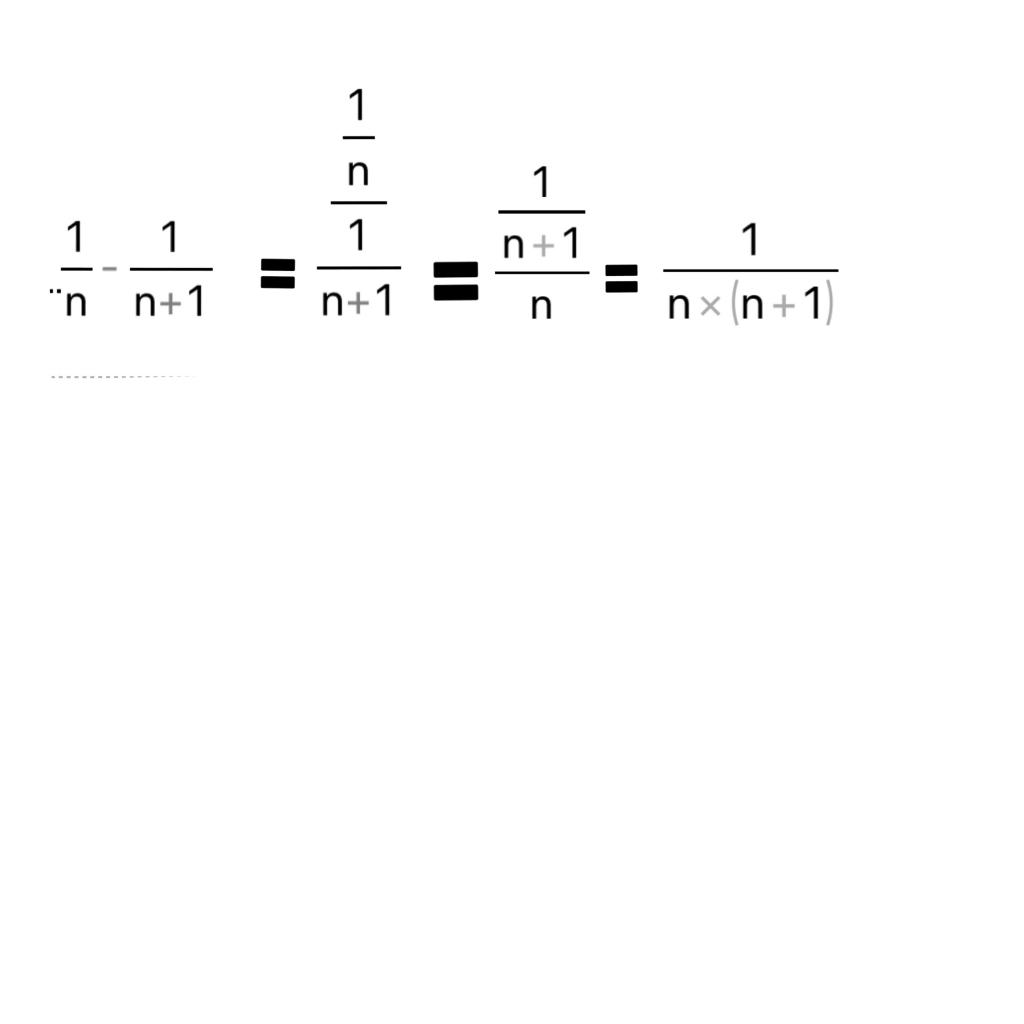
 . sérieux !
. sérieux !