Formule nombre de sommets sur des polygones adjacents

[vichente18]

Il y a cependant des choses qui te permettent d'en savoir d'autres.

Si tu commences par les formuler correctement tu pourras en déduire d'autres.

Reprends là ou l'on s'est arrêté tout à l'heure, tu as distinguer une relation entre Longueur et largeur qui t'as permis de trouver une relation entre nombre de carrés dans une longueur et nombre de carrés dans une hauteur.

Largeur = l Longueur=L
avec L=l+6

Tu sais que le nombre de carrés dans une longueur est de L/2 et le nombre de carrés dans une largeur est l/2.
Tu peux écrire nombre total de carrés = L/2 * l/2 et comme L=l+6 cela équivaut ((l+6)/2)*l/2 c'est aussi le nombre de cerisiers.

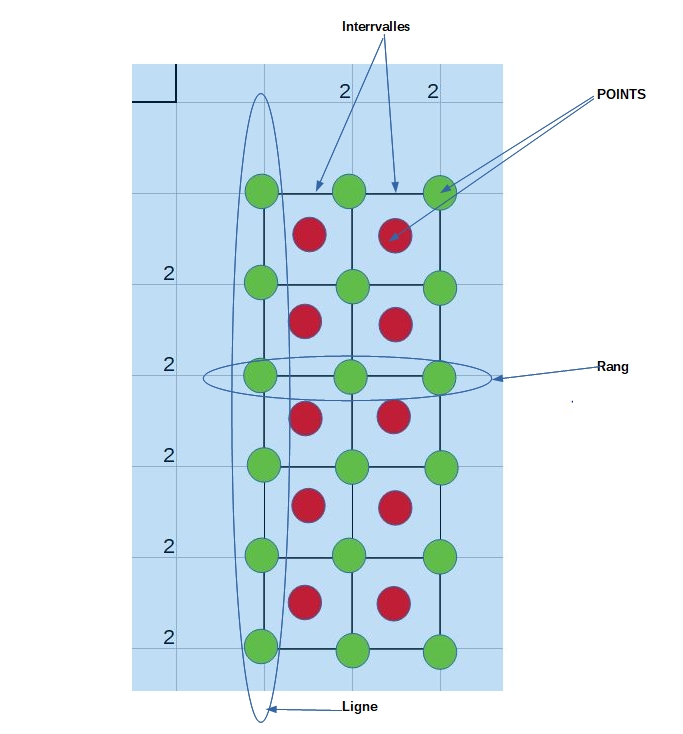
Ensuite si tu comptes les pommiers sur un rang en largeur tu ne compte plus des carrés mais des sommets qui se situent de part et d'autres des côtés des carrés qui forment la largeur de ce premier rang: tu commences donc par un sommet et termine ton rang par un sommet (un pommier) à ce stade il faut que tu regardes par toi même sur le dessin pour en déduire la formule du nombre de pommiers par rang en largeur puis le nombre de pommiers par rang en Longueur et enfin en déduire une formule du nombre total de pommiers.

Merci pour l'aide , je verrai ça demain maintenant pour enfin résoudre ce problème.
-----

[vichente18]

Bon,

maintenant que tu as répondu aux questions, il est facile de terminer ce que tu avais commencé :
"Soit n le nombre de carré[e]s [par] dans la largeur :

1ère rangée : 2n +2
2ème rangée et rangées suivantes : (n+1) p fois""
Et p est "le nombre de rangées , dans le sens de la largeur p rangées et dans le sens de la longueur p+3 rangées.
Qu'est-ce qu'il venait faire ici ? Tu parlais de carrés et je te parlais de carrés. Donc je ne sais même pas de quoi tu parlais (de rangées d'arbres ou bien de rangées de carrés ?
Et si n est le nombre de carrés dans la largeur (j'avais pris m, tu n'es même pas capable de lire ??? Ou de répondre sans tout mélanger ?), et m le nombre de carrés dans la longueur, une fois la première rangée de carrés prise, il en reste m-1 qui chacune nécessitent 2+n-1=n+1 points. Au total, sur les sommets, il y a 2n+2+(m-1)(n+1).

Voilà, ton problème de nombre de carrés est résolu, en appliquant les règles, en utilisant des notations simple et faisant simplement le calcul. En factorisant ce résultat, tu verras que la réponse est symétrique en m et n.

Avec ça ton problème est quasiment terminé, puisque tu as un lien entre m et n.

NB : "Oui mais gg0 je ne sais pas du tout pourquoi tu t'énerves" ?? Je ne suis pas énervé, je suis seulement atterré par ton attitude. Dire la vérité n'est pas s'énerver. Si on ne te dit pas que tu agis absurdement, tu ne le rectifieras pas (ça ne sert pas de s'excuser quand on a agi bêtement, c'est fait).

Cordialement.

Tes attaques personnelles n'ont aucun sens , surtout pour quelqu'un qui dit être atterré par mon attitude et donne des leçons alors que je ne rien fais de méchant premièrement , deuxièmement avant de donner des leçons aux autres on se regarde soit même tu n'es pas capable d'être poli . Je pose une question sur un forum et on ne s'est bien compris c'est tout , wahou c'est très grave . C'est toi qui est grotesque à être hystérique tout seul avec un motif qui ne justifie pas un tel cinéma franchement. C'est toi qui a une attitude bête , moi je parle de mathématiques depuis le début , toi tu me cherches des poux dans la tête. Alors garde tes petites réflexions , moi je n'embête personne.

[gg0]

"on ne s'est bien compris c'est tout" ?? On ne t'a pas compris, vu que tu ne posais pas la question qui t'intéressait.
"il n'y a que la vérité qui fâche"

[Liet Kynes]

je pense que ce qui serait intéressant c'est d'arriver à ce que vichente18 puisse écrire l'équation qui ne comporte qu'une seule inconnue pour solutionner.
Ainsi il comprendra les relations entre les éléments d'un quadrillage carrés, segments,points.

[vichente18]

je pense que ce qui serait intéressant c'est d'arriver à ce que vichente18 puisse écrire l'équation qui ne comporte qu'une seule inconnue pour solutionner.
Ainsi il comprendra les relations entre les éléments d'un quadrillage carrés, segments,points.

Bon sur ton dessin il y a 18 pommiers , 3 dans une largeur et 6 dans une longueur. Mais là je suis plus perdu qu'au début c'est facile de dénombrer mais j'arrive pas comment je peux mettre ça en formule. Bon en gros il y a (l+6)/2x l/2 arbres si on plante un au centre de chaque carré qui représente tes cerisiers en quelque sorte dans ton exemple donc cette expression doit etre équivalente à un truc du style 44+ 2x ( (l+6)/2)+2 + ( (l+6)/2) -1 multiplié par n rangées car je ne sais pas combien j'ai de rangées , mais ça me rajoute une variable ça me gonfle.

[vichente18]

"on ne s'est bien compris c'est tout" ?? On ne t'a pas compris, vu que tu ne posais pas la question qui t'intéressait.
"il n'y a que la vérité qui fâche"

Quelle vérité ? Ma question sur le nombre total de sommets est bien le concept majeur qui me bloque pour résoudre le problème c'est bel et bien la question qui m'intéresse depuis le départ . Tu brasses beaucoup de vent. Si ça te saoule de répondre , je peux le comprendre mais je ne t'ai pas forcé à m'aider.

[Liet Kynes]

Bon sur ton dessin il y a 18 pommiers , 3 dans une largeur et 6 dans une longueur. Mais là je suis plus perdu qu'au début c'est facile de dénombrer mais j'arrive pas comment je peux mettre ça en formule. Bon en gros il y a (l+6)/2x l/2 arbres si on plante un au centre de chaque carré qui représente tes cerisiers en quelque sorte dans ton exemple donc cette expression doit etre équivalente à un truc du style 44+ 2x ( (l+6)/2)+2 + ( (l+6)/2) -1 multiplié par n rangées car je ne sais pas combien j'ai de rangées , mais ça me rajoute une variable ça me gonfle.

Tu n'identifies pas et ne nommes pas correctement ce que tu comptes, On va reprendre à zéro.
Appelons rang les traits horizontaux du quadrillage
Appelons lignes les traits verticaux du quadrillage
Dans le premier rang tu peux compter 3 arbres (points) entre chaque arbre un intervalle.
Un intervalle est le segment qui permet de relier deux points entre eux.
Quand il y a 1 point combien d'intervalles?
Quand il y a 2 points combien d'intervalles?
Quand il y a 3 points combien d'intervalles?
Quand il y a x points combien d'intervalles? <-> Quand il y a x intervalles combien de points?

[vichente18]

Tu n'identifies pas et ne nommes pas correctement ce que tu comptes, On va reprendre à zéro.
Appelons rang les traits horizontaux du quadrillage
Appelons lignes les traits verticaux du quadrillage
Dans le premier rang tu peux compter 3 arbres (points) entre chaque arbre un intervalle.
Un intervalle est le segment qui permet de relier deux points entre eux.
Quand il y a 1 point combien d'intervalles?
Quand il y a 2 points combien d'intervalles?
Quand il y a 3 points combien d'intervalles?
Quand il y a x points combien d'intervalles? <-> Quand il y a x intervalles combien de points?

1 point = 0 intervalle
2 points = 1 intervalle
3 points = 2 intervalles
x points = (x-1) intervalles

[Liet Kynes]

x points = (x-1) intervalles

et donc x intervalles = x+1 points

Dans un quadrillage le premier intervalle du premier rang et le premier intervalle de la première ligne appartiennent au premier carré de ce quadrillage.
Que compte tu pour calculer le nombre de carrés? Quelle formule peux tu utiliser?

Sachant la relation entre intervalles et points, quelle formule pour calculer le nombre de points du quadrillage?
Si je place un point au centre de chaque carré combien de points vont se rajouter à ceux déjà présent?

[vichente18]

x points = (x-1) intervalles

et donc x intervalles = x+1 points

Dans un quadrillage le premier intervalle du premier rang et le premier intervalle de la première ligne appartiennent au premier carré de ce quadrillage.
Que compte tu pour calculer le nombre de carrés? Quelle formule peux tu utiliser?

Sachant la relation entre intervalles et points, quelle formule pour calculer le nombre de points du quadrillage?
Si je place un point au centre de chaque carré combien de points vont se rajouter à ceux déjà présent?

Bah par exemple pour le premier rang , le nombre d'intervalles me donne le nombre de carrés du premier rang. Ensuite le nombre d'intervalles du deuxième rang me donne le nombre de carrés pour le deuxième rang etc. Donc x multiplié par n rangées. Donc il y a x multiplié par n auquel on ajoute 1 pour avoir le nombre de points du quadrillage. Bah il y aura x points en plus.

[vichente18]

x points = (x-1) intervalles

et donc x intervalles = x+1 points

Dans un quadrillage le premier intervalle du premier rang et le premier intervalle de la première ligne appartiennent au premier carré de ce quadrillage.
Que compte tu pour calculer le nombre de carrés? Quelle formule peux tu utiliser?

Sachant la relation entre intervalles et points, quelle formule pour calculer le nombre de points du quadrillage?
Si je place un point au centre de chaque carré combien de points vont se rajouter à ceux déjà présent?

Et je pense qu'on s'est trompé dans la relation c'est pas x intervalles = x+1 points mais c'est x intervalles = x-1 points , j'ai fais le test j'ai mis deux carrés cote à cote je décompte 7 intervalles et 6 points seulement. Je comprends plus rien.

[Liet Kynes]

Et je pense qu'on s'est trompé dans la relation c'est pas x intervalles = x+1 points mais c'est x intervalles = x-1 points , j'ai fais le test j'ai mis deux carrés cote à cote je décompte 7 intervalles et 6 points seulement. Je comprends plus rien.

On ne s'est pas trompé.
Si tu n’essaies pas d'écrire cela sous la forme de formules et ne prends pas le temps (se concentrer) de bien tenir compte de comment ont été définis les termes tu ne vas pas avancer.
Relis le post 37 attentivement et réponds avec des formules pas avec des phrases.

Exemple :Un damier comporte 8 cases par 8 cases pour le jeu d’échecs , tout damier comporte x cases par x cases, la formule mathématique qui donne le nombre de cases est x*x

Dans quel cadre fais tu cet exercice?

[Liet Kynes]

Le schémas et ce que nous avons définis comme termes au post 37:

[Liet Kynes]

j'ai fais le test j'ai mis deux carrés cote à cote je décompte 7 intervalles et 6 points seulement. Je comprends plus rien.

Désolé je n'avais pas de temps pour corriger ce matin ce qui t'as induis en erreur: il s'agit de compter les intervalles et les points sur un même rang ou sur une même ligne comme définis sur le dessin.
Cette relation va servir après pour trouver une formulation à partir des indications de ton énoncé.