Géométrie Repérée 1ère

[boogie2466]

Bonjour,

on m'a donné un exercice à résoudre chez moi, sauf que je n'ai jamais fait ce type d'exercice, et donc je ne comprends pas clairement ce qui nous est demandé:

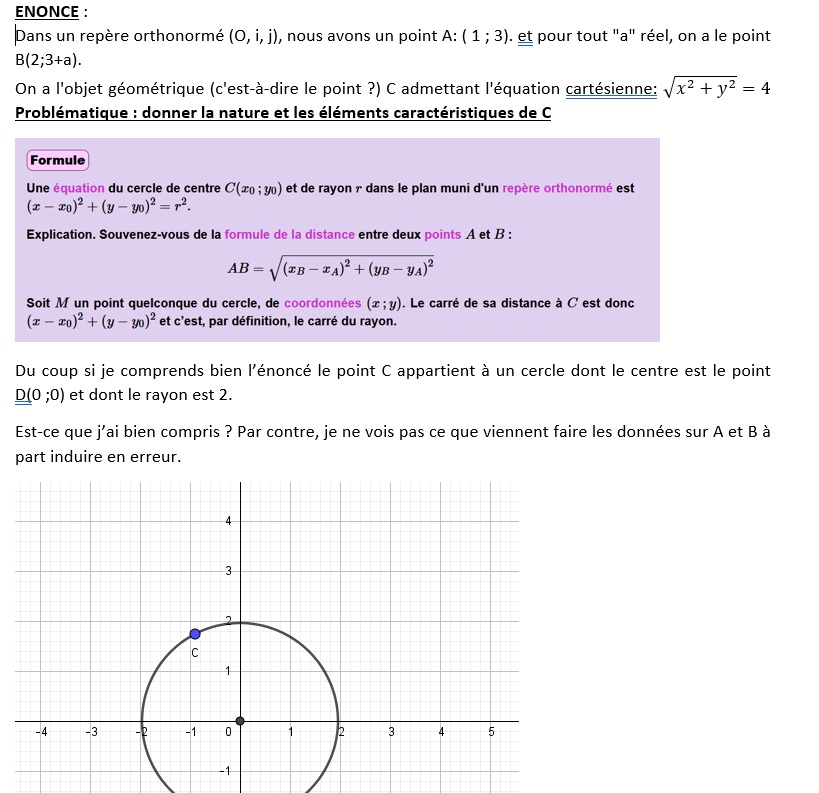
Dans un repère orthonormé (O, i, j), nous avons un point A: ( 1 ; 3). et pour tout "a" réel, on a le point B: (2 ; 3+a).
On a l'objet géométrique (c'est-à-dire le point ?) C admettant l'équation cartésienne: x au carré + y au carré = 4.

Nous devons donc donner la nature et les éléments caractéristiques de C. Sauf que je ne comprends pas de quels éléments il s'agit, et comment nous devons y procéder étant donné que je ne l'ai jamais fait. J'imagine que C est un point caractéristique sauf que je ne sais pas comment le déterminer ? Pourriez-vous m'aider svp?

Merci,
Bonne journée!
-----

[gg0]

Bonjour.

1) Apprends tes leçons. C'est le moyen simple de savoir faire les exercices d'application. Par exemple de savoir tout de suite ce que c'est que l'objet géométrique (C).
2) Appliques à cet énoncé, ça devrait venir tout seul.
3) Si tu as appris ton cours et appliqué et que tu bloques, reviens exposer ce que tu as vu ici, on t'aidera.

Bon travail !

NB : "je n'ai jamais fait ce type d'exercice" est une mauvaise raison. Tu es en apprentissage, c'est normal que tu aies des exercices que tu n'as jamais fait : Faire des maths, ce n'est pas imiter des corrections d'exercices, c'est appliquer le cours à des exercices nouveaux.

[jacknicklaus]

J'imagine que C est un point caractéristique sauf que je ne sais pas comment le déterminer ? !

Faut pas imaginer. Tu as x² + y² = 4. Pour quoi un seul point (donc un seul couple (x,y)) serait il solution de cette équation; Moi j'en vois plusieurs. Enormément même.

0² + 2² = 4
2² + 0² = 4
0² + (-2)² = 4
(-2)² + 0² = 4
(racine(2))² + (racine(2))² = 4
(-racine(2))² + (-racine(2))² = 4

etc etc (une infinité de solutions, en fait)


Si tu fais un dessin, que représente x² + y² ? As tu entendu parler de Pythagore ?

[boogie2466]

D'accord, mais je n'ai aucune mention dans mon cours de ce qu'est un objet géométrique...

pour x(au carré) + y (au carré), cela nous donne l'hypoténuse au carré d'un triangle rectangle. Oui j'avais compris pour l'équation cartésienne, mais je ne vois pas le rapport avec la nature et les éléments caractéristiques de C... Car ce n'est quand même pas des éventuelles coordonnées qu'il s'agit, si ? Et autrement, j'essaye de placer dans un repère les points seulement on a une inconnue "a" donc il est difficile, vu que le résultat changera selon sa valeur, de constater de caractéristiques... Mais merci beaucoup quand même! je vais continuer de chercher

[A voir en vidéo sur Futura]

[gg0]

Bonjour.

Les objets géométriques sont les choses qui ont un nom en géométrie (c'est du français, "objet") : points, droites, plans, triangles, carrés, cercles, etc.
Tu n'as pas dans ton cours les notions d'équation de droites ? D'équation de cercles ? Vue la question, ça m'étonnerait.
Tu vois mieux ?

Cordialement.

[jacknicklaus]

pour x(au carré) + y (au carré), cela nous donne l'hypoténuse au carré d'un triangle rectangle.

Oui, enfin c'est surtout la carré de la distance du point M (x,y) à l'origine de coordonnées (0,0)

Et donc cette distance au carré est une constante égale à 4, et donc ... tu vois mieux (copyright gg0) ?

[boogie2466]

Ah! Il s'agit de l'équation cartésienne d'un cercle de centre O de coordonnées (0;0), et de rayon r= 2, avec C point mobile appartenant au cercle . Donc quelles que soient les coordonnées de C, du fait qu'il peut représenter tout point du périmètre du cercle, le rayon au carré= 4 est constant. Je pense que c'est ça,,non?

Merci beaucoup ! J'ai conscience de toute l'aide que vous m'avez apporté... du coup je n'avais pas réellement de cours sur ce sujet, c'est un peu compliqué comme nous sommes une semaine sur deux au lycée il y a des cours qui nous sont envoyés mais c'est pas forcément facile de tout gérer pour les professeurs. Merci vraiment!
Bonne journée!

[boogie2466]

Bonjour, j'ai une autre question sur ce même thème qu'est la géométrie repérée: En effet, je sais comment trouver les coordonnées d'un point permettant l'intersection entre une droite et un cercle (système, résolution par substitution) seulement, comment trouver les coordonnées des points ne permettant aucune intersection, ou en permettant deux ? Car en effet, en résolvant ce système on obtient un résultat mais qui n'est du coup pas valable pour les deux autres, ainsi il y a forcément une autre méthode pour trouver les deux autres, non ? J'ai beau chercher partout dans mes cours, et sur internet je ne trouve pas... Pourriez-vous m'aider ?

[jacknicklaus]

trouver les coordonnées d'un point permettant l'intersection entre une droite et un cercle

Incompréhensible. L'intersection entre une droite et un cercle, çà je vois. Mais que viens faire ici "le point" ?

comment trouver les coordonnées des points ne permettant aucune intersection, ou en permettant deux ? Car en effet, en résolvant ce système on obtient un résultat mais qui n'est du coup pas valable pour les deux autres

Incompréhensible, désolé.

[gg0]

Je ne comprends pas ce que veut dire "un point permettant l'intersection entre une droite et un cercle ". Une droite et un cercle ont, suivant les cas, deux intersections, ou une ou aucune, et ces intersections sont des points. Mais comment un point peut-il permettre quelque chose ? De même, que peut vouloir dire "les deux autres" ?

Si c'est à propos d'un exercice, donne nous l'énoncé, qu'on puisse savoir de quoi tu parles. Là, c'est dans ta tête, mais on n'est pas télépathes.

Cordialement.

[boogie2466]

Cela suit ce que j'ai énoncé au début du post:
Nous avons donc une droite (AB) avec les coordonnées de A précisées, celles de B aussi mais avec une variable dans son ordonnée.

Donc nous avons une droite pouvant varier selon selon l'ordonnée de B. A: (1;3) B(2; 3+a). L'équation de cette droite est donc y= ax - a +3.
Nous avons l'équation cartésienne d'un cercle de rayon r=2 : x² + y² = 4

Pour trouver la valeur de "a" lorsqu'il y a qu'une seule intersection entre ces deux objets géométriques, on utilise un méthode de résolution par substitution du système regroupant ces deux équations, donc j'obtient une unique solution a=-3. Mais autrement, pour déterminer la ou les valeurs de cette variable lorsqu'il n'y a pas d'intersection, ou alors qu'il y en a 2, je ne vois vraiment pas comment faire ?

[gg0]

Donc voilà l'énoncé. Maintenant on peut comprendre de quoi tu parles.

Donc tu cherches à savoir pour quelles valeurs de a (qui donne le point B) il y a une, 2 ou 0 intersections de (AB) avec le cercle.
En substituant y dans l'équation du cercle, tu obtiens une équation du second degré (quel que soit a). Il y aura 2 points d'intersection si cette équation a deux solutions (2 valeurs de a = 2 droites). Dans quel cas une équation du second degré a-t-elle 2 solutions ? Et il n'y aura pas de point d'intersection si cette équation n'a pas de solution. Dans quel cas une équation du second degré n'a pas de solution ?

Si tu veux entrer dans les détails, expose tes calculs.

[jacknicklaus]

donc j'obtient une unique solution a=-3.

gnéé ??

expose tes calculs , car ce que tu annonces est signe d'incompréhension du problème posé.

[boogie2466]

J'aile système:

y=ax-a+3
x² + y² = 4

J'utilise l'abscisse du point B (2; 3+a)

y= 2a-a +3 = a+3

donc je substitue:

4 + (a + 3)² = 4
a² + 6a +9= 0

On cherche le discriminant du trinome: avec a = 1, b= 6 et c=9

Il vaut 0 il y a donc une unique solution. x= -6/2 = -3

[boogie2466]

Oui mais dans ce cas là pourquoi on n'utilise pas l'abscisse déjà déterminée de B, x=2 ?

Elle a 2 solutions si son discriminant est supérieur à 0, et elle n'en a pas lorsqu'il est inférieur à 0

[jacknicklaus]

J'utilise l'abscisse du point B (2; 3+a)

y= a+3

donc je substitue:

4 + (a + 3)² = 4
unique solution. x= -3

DOnc là, tu as trouvé le paramètre a pour qu’un point B de coordonnées (2, 3+a) appartienne au cercle.

C'est quoi le rapport avec la question posée, qui est je le suppose (tu ne t'es jamais donné la peine de recopier complètement ton énoncé) : discuter, en fonction du paramètre a, du nombre d'intersections entre la droite AB et le cercle. ?

réponse : aucun rapport.

[gg0]

Boogie2466,

tu n'as pas du tout résolu le système par substitution. Pourquoi n'as-tu pas traité le système ???
De ce fait, on ne peut même pas t'aider à comprendre (*), tu ne cherches pas les intersections de la droite et du cercle, données par le système :
y=ax-a+3
x² + y² = 4.

A toi de recommencer sérieusement la résolution de ce système, qui donne les éventuelles coordonnées des intersections.


(*) et même, ce qu'on t'a dit, croyant que tu faisais le bon travail, n'a pas d'intérêt.

[boogie2466]

D'accord, du coup cela me donne:

(ax-a +3)² + x² -4= 0

donc en développant: "(ax)² + a² + 9 - 2.ax. (-a).3" +x² -4=0

(ax)² + a² + 9 + 6a²x + x² -4=0

J'organise: (ax)² + x² + 6a²x + a²+5=0, j'ai donc un trinôme du 2nd degré avec : a= a²+1, b=6a², et c= a²+5.

Donc après, je sais que si le discriminant est supérieur à 0 il y a 2 solutions, si il est égal à 0 il y 1 solution et si il est inférieur à 0, il n'y en a pas.

Donc si je comprends bien lorsque le trinôme a 2 solutions, il y 2 intersection entre (AB) et le cercle, lorsqu'il y en a qu'une il y a 1 intersection, et lorsqu'il n'y a pas de solution il n'y a pas d'intersection ? mais du coup il faudrait résoudre des inéquations avec le discriminant pour savoir pour quel a il est supérieur, inférieur ou égal à 0?

Mais là je bloque, j'essaie de résoudre depuis hier soir mais à chaque fois je tombe sur des valeurs qui m'emmènent nul part...mais c'est sans doute que je n'ai pas la bonne méthodologie...

Après, j'ai essayé résoudre les inéquations, avec les formules des solutions pour les différents discriminants ( -b/2a...) mais c'est pareil je tomba pas non plus sur des résultats cohérents...

[gg0]

Bonjour.

Tu t'es trompé en développant le polynôme :
(ax-a+3)²+x²-4 =0
(ax+(3-a))²+x²-4 =0
(ax)²+2ax(3-a)+ (3-a)² + x² -4 = 0
(a²+1)x²+2a(3-a) x + (3-a)²-4 = 0
Malgré la complexité des coefficients, le discriminant se simplifie bien et est du second degré en a.

Bon travail !

[boogie2466]

D'accord, merci beaucoup! Donc j'ai trouvé un discriminant de : ²

Je calcule donc de nouveau le discriminant de ce trinôme (alors égal à 964) pour connaitre les valeurs de a pour lesquels le premier discriminant est inférieur, supérieur, ou égal à 0 :

il n'y a pas d'intersection lorsque que a appartient à ]x1;x2[ car le coefficient a est positif, donc dans cette intervalle a est négatif ,
il y a 1 intersection, avec les solutions x1 et x2 annulant le trinôme
il y a 2 intersections, quand a appartient à ]-infini;x1[ et ]x2; +infini[

Est-ce donc bien cela ?
Autrement, je vous remercie énormément de l'aide que vous m'avez apporté, et du temps que vous m'avez consacré! Cela m'a permis de comprendre énormément de choses que je n'avais pas compris en cours.

[boogie2466]

Excusez moi il y a une petite erreur de frappe : le premier discriminant que j'ai trouvé est égal à : 12a² + 24 a -20

[gg0]

Oui, c'est ça, et il est facile de savoir pour quelles valeurs de a c'est nul, négatif ou positif.

Bon travail !

[david_champo]

J'ai essayé de faire l'exercice mais je comprends rien à ce que vous avez fait. Est ce que quelqu'un peut me dire où j'ai fais une erreur dans mon raisonnement.
Bonne journée,
David_Champo

[boogie2466]

Bonjour,
c'est bien ça.
A et B sont des informations qui servent pour la deuxième partie de l'exercice, que nous avons traité à la fin du post.

Bonne journée à vous!

[david_champo]

J'ai essayé de faire la suite car je n'ai rien compris à vos réponses. Est ce que j'ai fais des erreurs ?

[david_champo]

Voilà le résultat que j'ai trouvé.

[gg0]

David_champo,

les règles du forum sont claires, on n'est pas là pour faire les exercices des questionneurs. Encore moins quand ils ont su faire et l'ont dit.
Si tu veux résoudre les problèmes qui sont posés, libre à toi de le faire chez toi, mais pas ici, encore moins avec des erreurs comme sur un autre fil. Ou en nr répondant pas a&ux questions, et de manière incorrecte comme ci-dessus.
Tu pollues le fil de Boogie2466.

[david_champo]

Bonjour,
Ok. Pas de problème. Je ne referais plus cela. C'était juste que j'étais très intéressé par le problème. Et du coup, je suis peut-être allé trop loin. Je vous demande pardon. C'est juste que je trouvais les réponses trop calculatoires à mon goût. Je crois que je suis trop littéraire pour les mathématiques. J'adore rédiger.
Bonne journée à vous
David Champo