Questions sur: Y(x)=3^x -2*x -1 est multiple de 4 quel que soit x, entier

[SULREN]

Bonsoir,
Comme beaucoup d’autres « vieux » je m’intéresse aux petites énigmes mathématiques qui nous sont proposées dans les revues afin de nous permettre de vérifier que Alzheimer, est certes derrière la porte, mais qu’il n’a pas encore glissé le pied dans l’entrebâillement.

Hier soir j’ai trouvé comme énoncé :
« Choisissez un chiffre x. Sauriez-vous ensuite élever 3 à la puissance x ? Sauriez-vous maintenant enlever 2 fois x puis à ce premier résultat ? Vous obtenez alors un multiple de 4, n’est-ce pas ? Pourquoi cela ? »
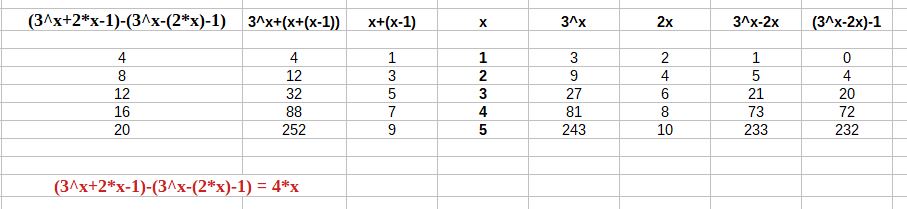
En d’autres termes : expliquer pourquoi Y(x) = 3^x - 2*x -1 est toujours un multiple de 4, quel que soit x entier positif >= 1.

Je suis allé au dodo en me disant (prétentieux le mec ) que le temps de faire un bref « décubitus dorsal » pour permettre à ma vieille carcasse de se décontracter, le cerveau aurait résolu le petit problème (comme c’est souvent le cas, tant ils sont faciles)
1ere piste :
Ce doit être un truc du genre : 3^x est impair quel que soit x, donc 3^x -1 et pair et comme 2*x est pair la somme est pair…..oui…. mais pas nécessairement multiple de 4. Loupé mon bonhomme !
2eme piste :
La résolution analytique de Y(x) = 4*N afin de démontrer que pour tout x il existe un N entier.
Oui…... mais j’ai séché.
3eme piste :
Il suffit de partir d’un Y(x) multiple de 4 et de démontrer que Y(x+1) est un multiple de Y(x) donc forcément un multiple de 4
Calcul mental : Y(1)=0, Y(2)=4, Y(3)=20, Y(4)=72
Re-loupé.
4eme piste : Après un « accroche-toi Jeannot !»
Comme : Y(1)=0, Y(2)=4, Y(3)=20, Y(4)=72, ……
Je fais un petit raisonnement par récurrence.
Si partant de Y(x) étant multiple de 4, je démontre que Y(x+1) est aussi multiple de 4 c’est bon.

Impossible à faire mentalement……donc dodo, déçu ….un peu vexé…..et dès le réveil papier crayon et ……après quand même un bon moment de réflexion.
Relation 1 : Y(x) = 3^x -2*x -1 = 4*N
Relation 2 : Y(x+1) = 3^(x+1) -2*(x+1) -1 = 4*K avec la question existe-t-il un K entier ?
Après développement la Relation 2 devient :
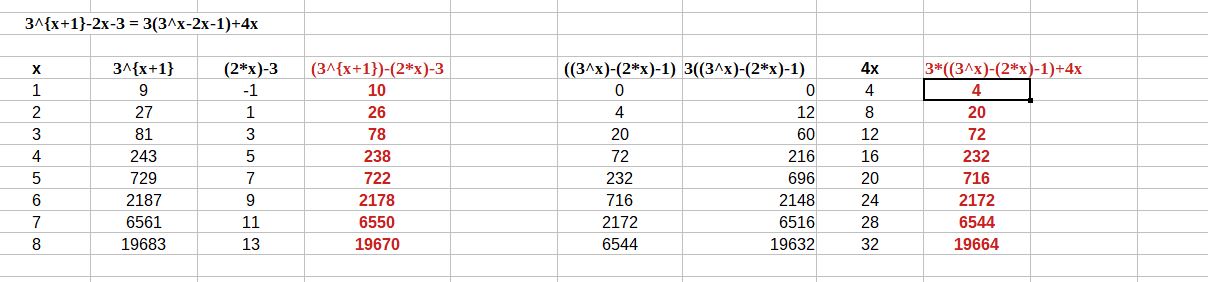
Relation 3 : Y(x+1) = 3*3^x -2*x -3 = 4*K

En soustrayant de la Relation 3, trois fois la relation 1, afin d’éliminer les puissances x, on aboutit à :
-2*x + 6*x = 4*K – 12*N
Soit : x = K – 3*N
On a prouvé qu’il existe bien un K qui est un entier et on a :
Y(x+1) = 3^x -2*(x+1) -1 = 4*K confirmant que Y(x+1) est aussi un multiple de 4. Cqfd.

Vérif :
Y(4) = 72 = 4*18 c’est-à-dire avec x= 4 et N=18
Pour Y(5) on part de x=4 donc : K=x+3*N = 4+54 = 58
C’est bien le cas :
Y(5) = 3^5 – 2*5 -1 = 243 -10 -1 = 232 = 4*58

Le but de mon message n’était pas d’exhiber mes galipettes, mais de vous poser les questions suivantes :
Question 1 : Peut-on affirmer (axiome) que 3^x est toujours impair (C’était ma piste 1)
Question 2 : Existe t’il une résolution analytique du problème posé dans l’énoncé, autre que le raisonnement par récurrence.
Question 3 : Mon raisonnement par récurrence est-il réellement correct ?
Question 4 : Je pense avoir démontré que Y(x) est toujours un multiple de 4, mais je n’ai pas répondu à la question posée dans l’énoncé : « Pourquoi cela » ? Elle laisse penser qu’il existe une explication bien plus évidente que mon raisonnement. Laquelle ?

Merci d’avance pour vos réponses.
-----

[danyvio]

Je sors du dodo et trouve ton message.

Une piste : 3 = -1 mod(4), donc 3^x=(-1)^x mod(4)

Si x pair 3^x=1 sinon = -1

Je reviens après le petit déj

[Liet Kynes]

Bonjour,

S'endormir en faisant des calculs c'est bien agréable..

Peut-on affirmer (axiome) que 3^x est toujours impair (C’était ma piste 1)

Si tu développes 3^x: 3*3.. x fois, tu te rends compte que tu multiplies un nombre impaire par un nombre impaire opération dont le résultat est toujours non paire.

[danyvio]

Je reprends le flambeau : il faut partir sur les congruences modulo 4 de 3^x et de -2x . Deux cas : x pair et x impair.

Je ne développe pas davantage pour ne pas mâcher le travail des jeunes

[A voir en vidéo sur Futura]

[gg0]

Bonjour.

L'énoncé est bizarre, pourquoi dire "un chiffre x" ? D'abord, c'est faux pour le chiffre 0, ensuite c'est vrai pour tout entier au moins égal à 1.

Question 1 : Ce n'est pas un axiome, mais une propriété arithmétique très classique (unicité de la factorisation en entiers premiers) : les seuls facteurs premiers de Y(x) sont des 3, donc 2 n'est pas un facteur de Y(x)

Question 2 : Tu veux dire une preuve directe ? On verra à la fin.

question 3 : Non, car tu utilises la conclusion ("Y(x+1) = 3^(x+1) -2*(x+1) -1 = 4*K ") pour la démontrer !! (*) Cependant, ce que tu as fait donne une piste de rédaction d'une preuve correcte (**)

Question 4 : Il y a peut-être plus simple, mais on voit que si x est pair, ça revient à justifier que 3^x-1 est un multiple de 4 (puisque 2x l'est). On fait deux cas :
* x impair : x=2n+1 avec n entier positif (puisque x=0 est exclu)
(***)
* x pair : c'est plus simple, je te laisse faire, avec les mêmes idées.

Cordialement.

(*) En notant H(x) l'hypothèse de récurrence, tu as prouvé (H(n) et H(n+1) ==> K est un entier); or cette implication est vraie (donc démontrable) si H(n+1) est fausse. Donc sa véracité ne dit rien de celle de H(n+1).
(**) De la forme H(n) ==> H(n+1)
(***) La parenthèse après le (9-1) se réduit à (9+1) pour n=2 et à (1) pour n=1.

[SULREN]

Bonjour,
Merci à tous pour vos réponses.
@gg0 : je répondrai bien sûr à tes remarques, dans un post à venir.

Je voudrais d’abord poster une solution au problème qui m’est venue à l’idée…..avant qu’un plus vif que moi me grille
Elle est encore plutôt basée sur la récurrence, que sur la pure congruence (mais je continue à phosphorer sur cette dernière).
Y(x) = 3^x –2*x -1
Y(x+1) = 3*3^x – 2x -2 -1
Donc :
Y(x+1) – Y(x) = 2*3^x -2 = 2*(3^x-1) = 2*2*(n) => modulo 4
Puisque 3^x -1 est forcément pair et peut s’écrire 2*n avec n entier.

Chaque fois que x augmentera de 1 on aura Y(x) qui augmente d’un multiple de 4.
Comme Y(1)=0 et Y(2)=4…… on n’aura que des multiples de 4 lorsque x croîtra jusqu'à l'infini.

[Médiat]

Bonjour,

Plusieurs méthodes :

1) récurrence,
2) congruence
3) et c'est celle qui explique le mieux le "pourquoi", il suffit de remarquer que 3 = 4 - 1 (et un tout petit calcul)

[Liet Kynes]

Je fini par tomber sur une relation en développant avec le tableur

 Cliquez pour afficher

(3^x+2*x-1)-(3^x-(2*x)-1) = 4*x




Le truc qu'il me manque c'est de transformer ces résultats en démonstration

[SULREN]

Re Bonjour,
Je réponds au post#5 de gg0, déjà par correction comme il se doit, mais surtout parce que je considère qu’on me rend service en me « rappelant à l’ordre » en matière de rigueur dans l’usage des mots et dans la structuration des raisonnements. D’où un remerciement.

L'énoncé est bizarre, pourquoi dire "un chiffre x" ? D'abord, c'est faux pour le chiffre 0, ensuite c'est vrai pour tout entier au moins égal à 1.

Tout à fait d’accord, cet énoncé est bizarre. Le texte était :
« Choisissez un chiffre x. Sauriez-vous ensuite élever 3 à la puissance x ? Sauriez-vous maintenant enlever 2 fois x puis 1 à ce premier résultat ? Vous obtenez alors un multiple de 4, n’est-ce pas ? Pourquoi cela ?»
Le « 1 » a sauté quand j’ai tapé mon message parce que mon clavier n’était pas en mode numérique. Désolé, J’aurais dû me relire avec plus d’attention.
C’est moi qui ai ensuite reformulé cet énoncé sous la forme ci-dessous, plus condensée, tout en étant plus précise (ajout de x partant de 1 et restant positif) :
En d’autres termes : expliquer pourquoi Y(x) = 3^x - 2*x -1 est toujours un multiple de 4, quel que soit x entier positif >= 1.

Je pense que l’auteur de cet énoncé à défini x comme « un chiffre x » parce qu’il est tombé dans la mauvaise habitude, que l’on constate partout et dans les médias, de chercher à tout prix à être compris par « le lecteur de base », mais avec la base la plus basique possible. On tire donc tout le monde vers le bas au lieu d’essayer de remonter ceux qui sont en dessous de la moyenne.
Pour le vulgus pecum « un chiffre x » signifie : 0, ou 1, ou 2, …jusqu’à 9, donc un entier positif, certes limité à 9.
Il aurait été préférable de dire « x entier positif dans l’intervalle 1 à l’infini ».
Le vulgus pecum n’aurait peut-être pas bien compris, mais à mon avis il n’aurait pas fait partie de ceux qui désiraient prêter attention à ce type d’exercice.

Question 1 : Ce n'est pas un axiome, mais une propriété arithmétique très classique

Oui j’ai employé le mot axiome dans le sens ancien de « proposition évidente » alors qu’il a évolué, et pas seulement en mathématiques, vers le sens de : « énoncé, proposition posés à la base d’une théorie », ……reléguant le « 3^x est toujours un nombre impair » au rang d’une propriété.

Question 2 : Tu veux dire une preuve directe ? On verra à la fin.

Il est absolument évident que Y(x) objet de cette discussion, est un multiple de 4, pour tout x {1 ; ∞}. On s’en rend vite compte par des calculs effectués à la main, ou sur tableur, ou en écrivant quelques lignes de code et ceci jusqu’à la limite des nombres entiers manipulables par l’informatique.

Face à cet évidence et de suite après l’avoir constatée, j’ai cru (à tord) qu’un petit raisonnement simple, fait « au plumard » et même sans aucun coup de pouce de Morphée, me conduirait vite au « pourquoi de la chose ». C’était ma Piste 1, ou la 4 : résolution de l’équation :
(3^x -2*x -1)/4 = N montrant que N est un nombre entier quel que soit x.

question 3 : Non, car tu utilises la conclusion ("Y(x+1) = 3^(x+1) -2*(x+1) -1 = 4*K ") pour la démontrer !! (*) Cependant, ce que tu as fait donne une piste de rédaction d'une preuve correcte.

Je n’ai en effet pas dit: «je considère que la propriété est vraie pour x, et j’en ai des exemples, je vais démontrer qu’elle est vraie aussi pour x+1 et donc qu’elle est héréditaire».
J’ai dit : «si la propriété est vraie aussi au rang x+1, alors K doit être un entier. Puis l’expression de K à laquelle j’ai abouti a montré que c’était un entier. K=x+3*N (x et N étant déjà définis comme des entiers) ».

Mais j'admets qu’il faut (et tout particulièrement en mathématiques) être de la plus grande rigueur dans le raisonnement.

[SULREN]

Re,
Je vais essayer d'avoir une approche rigoureuse.

Gg0 a écrit au post#5:

Cependant, ce que tu as fait donne une piste de rédaction d'une preuve correcte (**)

(**) De la forme H(n) ==> H(n+1)

Je pars de Y(x) = 3^x -2*x -1 = 4*N signifiant que Y(x) est un multiple de 4, puisque N est défini comme entier. C’est l’hypothèse de départ.

Je multiplie par 3 et j’obtiens donc:
=> 3*3^x -6*x -3 = 12*N
3^(x+1) – 2*x -3 = 12*N +4*x
3^(x+1) – 2*(x +1) -1 = 12*N +4*x = 4*K en posant K=3*N+x.

Le premier membre n’est autre que Y(x+1),
3*N+x est forcément un entier, donc K aussi.
Cela signifie que Y(x+1) est aussi un multiple de 4 ; CQFD

C’est plus rigoureux….mais cela reste «capillo-tracté» et pas aussi évident, pas aussi Inspecteur Bourrel : « bon sang mais c’est bien sûr !», que ce que je cherche.

[jacknicklaus]

pas aussi Inspecteur Bourrel : « bon sang mais c’est bien sûr !», que ce que je cherche.

Voir réponse post #2, donnée par l'Inspecteur Danyvio.

[gg0]

Sulren,

c'est pour cela que je disais " ce que tu as fait donne une piste de rédaction d'une preuve correcte". En maths, on a besoin de preuves bien rédigées, pour être totalement sûr. On peut évidemment expliquer d'où sort une preuve (parfois d'un calcul intuitif faux !!), mais la preuve doit être sans défaut.
Dans ton cas, ce n'est pas si étrange que cela : multiplier par 3 est naturel pour passer de 3^x à 3^(x+1) qui est dans ce qu'on veut prouver. C'est donc assez naturel de multiplier par 3 toute l'inégalité.

Cordialement.

[danyvio]

Voir réponse post #2, donnée par l'Inspecteur Danyvio.

Restez simple, appelez-moi "maître".

[Médiat]

pas aussi Inspecteur Bourrel : « bon sang mais c’est bien sûr !», que ce que je cherche.

Comme dit plus haut : 3 = 4 - 1

[SULREN]

Bonsoir,

@Mediat :

Comme dit plus haut : 3 = 4 - 1

Ah mon bon monsieur, j'appartiens à l'ensemble des vioques au cerveau lent !
J’examine: 3^x -2*x -1.
Hypothèse: x est pair:
Sauf erreur, je sais mettre 3^x -1 sous la forme : 4*(polynôme) , dans cette hypothèse. Donc 3^x -1 est modulo(4) et pas seulement obligatoirement pair comme on l’a déjà dit précédemment.
Le 2*x est bien sûr aussi modulo (4).

Hypothèse: x est impair:
Sauf erreur, je sais mettre 3^x sous la forme: 4*(polynôme) -1
Le -1 restant s'ajoute à: -2*x -1 ce qui nous fait : -2*x -2 en principe aussi modulo(4)
Donc l'ensemble serait là aussi modulo(4)

Je revois tout cela, si ce n'est au plumard, ....devant un petit verre de remontant (*)....et je préciserai la solution au bien j'avouerai humblement avoir navigué sur l'oued qui finit dans le désert.

@ gg0 :

On peut évidemment expliquer d'où sort une preuve (parfois d'un calcul intuitif faux !!), mais la preuve doit être sans défaut.

Je n’ai qu’un petit niveau en mathématiques mais j’ai toujours pleinement adhéré à leurs exigences de formalisme et de rigueur dans le raisonnement. C’est même très formateur et utile dans tous les autres domaines.
Maths et physique ont toujours été mes matières d’excellence depuis le primaire jusqu’à la fin de mes études d’ingénieur. Mais ces dernières ne procurent qu’un tout petit niveau en maths, en comparaison de celui des mathématiciens. Par exemple, je m’intéresse beaucoup aux travaux d’Henri Poincaré (problèmes des 3 corps, sensibilité aux conditions initiales, section de Poincaré,....) mais je n’en prends connaissance qu’à travers des ouvrages de vulgarisation et des conférences (dont celle de C. Villani).

Je continue encore à bricoler en maths, par pur amour de cette discipline et pour les besoins de mes hobbies, donc pour des besoins de physique en fait : oscillateurs, horlogerie, horloges astronomiques, méca-céleste, méca des fluides, thermodynamique, etc.
Ces besoins n’obligent pas à maîtriser la résolution analytique et se contentent des résultats donnés par les méthodes numériques. J’ai réalisé par codage des outils puissants qui couvrent bien mes besoins et je peux même me passer de Matlab (trop cher) et de Scilab (gratuit et que j’ai installé).
Il faut quand même bien sûr savoir mettre correctement en équations le problème à traiter.

(*) to use with moderation of course

[SULREN]

Précision:

(*) to use with moderation of course

as Sir Isaac Newton himself would have said.

[SULREN]

Bon premier jour d’hiver,

Vous avez compris que je n’avais pas ci-dessus évoqué Newton juste pour faire plaisir aux Anglais qui nous Brexitent et nous envoient un variant inquiétant, mais parce qu’avec son binôme Newton avait répondu à ma recherche d’une solution analytique au problème posé.

Dans mon premier post j’avais écrit :

2eme piste :
La résolution analytique de Y(x) = 4*N afin de démontrer que pour tout x il existe un N entier.
Oui…... mais j’ai séché.

Mais c’est Mediat qui m’a mis sur la piste du binôme au post#7

Plusieurs méthodes :
1) récurrence,
2) congruence
3) et c'est celle qui explique le mieux le "pourquoi", il suffit de remarquer que 3 = 4 - 1 (et un tout petit calcul)

Il suffit en effet de remplacer 3^x par (4-1)^x dans Y(x) = 3^x -2*x -1
On voit de suite par l’expression générale du binôme de Newton et sans avoir à la développer, qu’on arrive à :
Y(x) = 4*(Polynôme1) + (+ou-)1 - 2*x -1
Le (+ou-)1 est égal à +1 si x est pair et à -1 si x est impair.

Cela finit donc toujours par :
Y(x) = 4*(Polynône2)
Qui répond par un « bon sang mais c’est bien sûr » à la question dans l’énoncé du problème (post#1): « pourquoi cela »

Me reste quand même encore à trouver la piste de la congruence.

PS : je vais réviser l’éditeur Latex pour écrire l’expression générale du binôme dans :
Y(x) = (4-1)^x -2*x -1

[Médiat]

Bonjour,

Il suffit en effet de remplacer 3^x par (4-1)^x dans Y(x) = 3^x -2*x -1

C'est bien cela, et il n'y a pas vraiment besoin du binôme de Newton pour voir que

Me reste quand même encore à trouver la piste de la congruence.

C'est la plus simple, pas la plus courte, la plus "bourrin", il s'agit, bien sûr d'étudier les congruences modulo 4

[jacknicklaus]

Y(x) = 4*(Polynôme1) + (+ou-)1 - 2*x -1

Manque de rigueur ici.

D'une part, "Polynôme1" n'est pas un polynôme. Un polynôme en x, c'est du xⁿ, pas du n^x D'autre part, mettre 4 en facteur dans une expression algébrique n'est pas suffisant pour prouver une divisibilité par 4.
Par exemple x²+1 = 4*(x²/4 + 1/4)

[SULREN]

Manque de rigueur ici.

Tout à fait. Mea culpa.
J’ai écrit cela par négligence notoire et je l’ai vu à la relecture, mais sans pouvoir le corriger parce que sur le forum Futura Sciences on ne peut corriger qu’une fois et qu’ensuite il faut passer par la Modération (Et j’avais utilisé le « une fois » pour un problème de forme : ajouter les balises Quote).

J'oublie cela à cause de la mauvaise habitude acquise sur mes autres forums : Horlogerie Suisse (inscrit en 2005), Usinages (inscrit en 2009), Webastro, et quelques autres, qui permettent de corriger autant de fois qu'on veut, même des années après. Il apparait juste la date de la dernière correction en bas du post.
Avant d’envoyer un message sur Futura Sciences mieux vaudrait le relire plusieurs fois, suffisamment espacées dans le temps (donc l’écrire sous Word et pas directement sous l’éditeur du forum). Mais on a envie de répondre très vite, comme je le fais avec le présent message.

J’aurais corrigé pour remplacer « polynôme » par « expression » en précisant que cette expression était une somme de nombres entiers, donc un entier. J’avais d’ailleurs bien écrit cela dès mon premier post :

La résolution analytique de Y(x) = 4*N afin de démontrer que pour tout x il existe un N entier.

[Livai91]

Bonjour,

Par récurrence pour tout entier >=1

On a pour x=1 vrai, supposons soit x entier >=1 tq 3^x-2x-1 multiple de 4 alors on a 3^{x+1}-2x-3 = 3(3^x-2x-1)+4x D'après l'HR le membre de gauche est multiple de 4 et on a le membre de droite multiple de 4 donc vrai quelque soit x entier >=1

[Liet Kynes]

Bonjour,

Par récurrence pour tout entier >=1

On a pour x=1 vrai, supposons soit x entier >=1 tq 3^x-2x-1 multiple de 4 alors on a 3^{x+1}-2x-3 = 3(3^x-2x-1)+4x D'après l'HR le membre de gauche est multiple de 4 et on a le membre de droite multiple de 4 donc vrai quelque soit x entier >=1

As tu vérifié?

[jacknicklaus]

As tu vérifié?

apparemment oui. et toi ?

[Liet Kynes]

apparemment oui. et toi ?

J'ai un écart de 6

[jacknicklaus]

tu dois t'emmêler les crayons quelque part. Si tu veux, poste ton calcul car je ne vois pas de quel 6 tu peux bien parler.

[Liet Kynes]

Je l'ai fais au tableur en détaillant:

[Livai91]

3^2-2-3 = 4 à gauche en rouge et pas 10 l'erreur viens du fait que vous faites la différence de 3^{x+1} et de (2*x)-3 ce qui est faux

Cordialement,

[jacknicklaus]

Tu souhaites calculer 3^(x+1) - 2x - 3

Mais tu calcules tout autre chose : 3^(x+1) - (2x-3) soit encore 3^(x+1) - 2x + 3

d'où l'écart de 6.

[Liet Kynes]

Oui j'ai trouvé mon erreur.. reste à voir si la relation que j'ai trouvé avant est la même du coup..