Vérifier un décagone
Bonsoir,
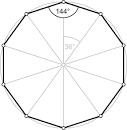
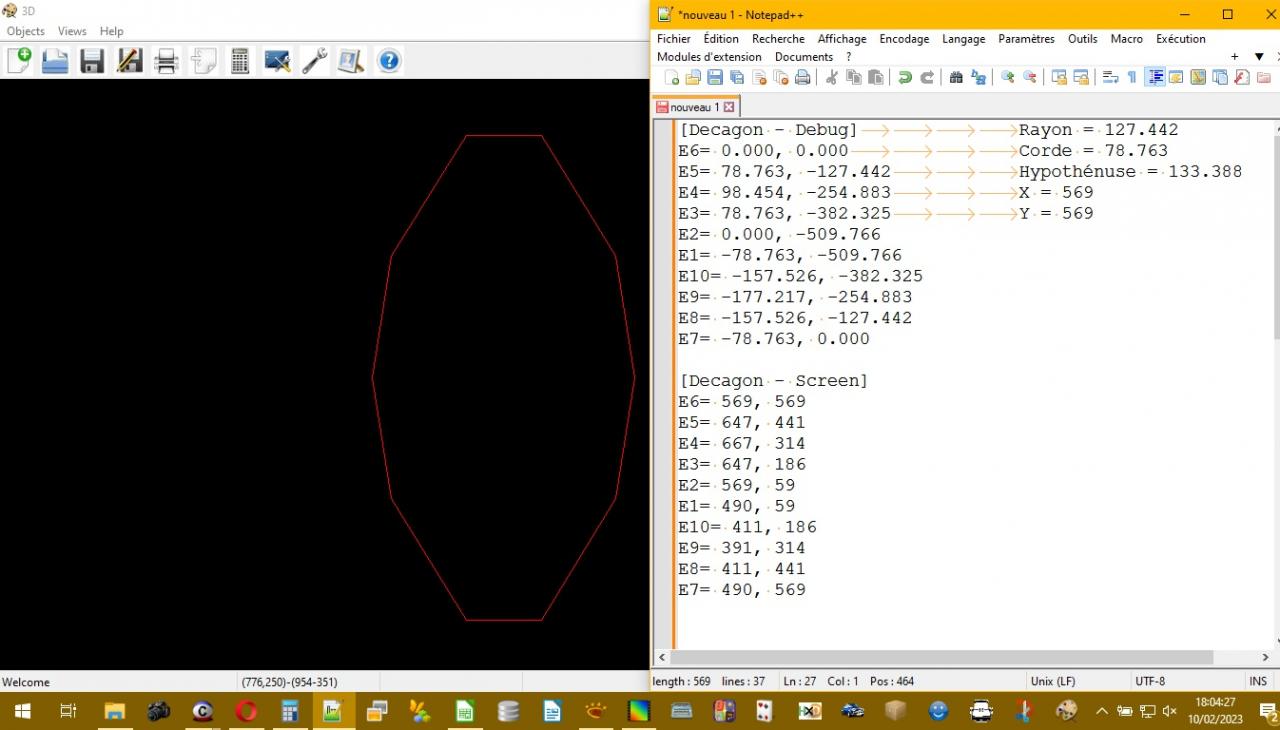
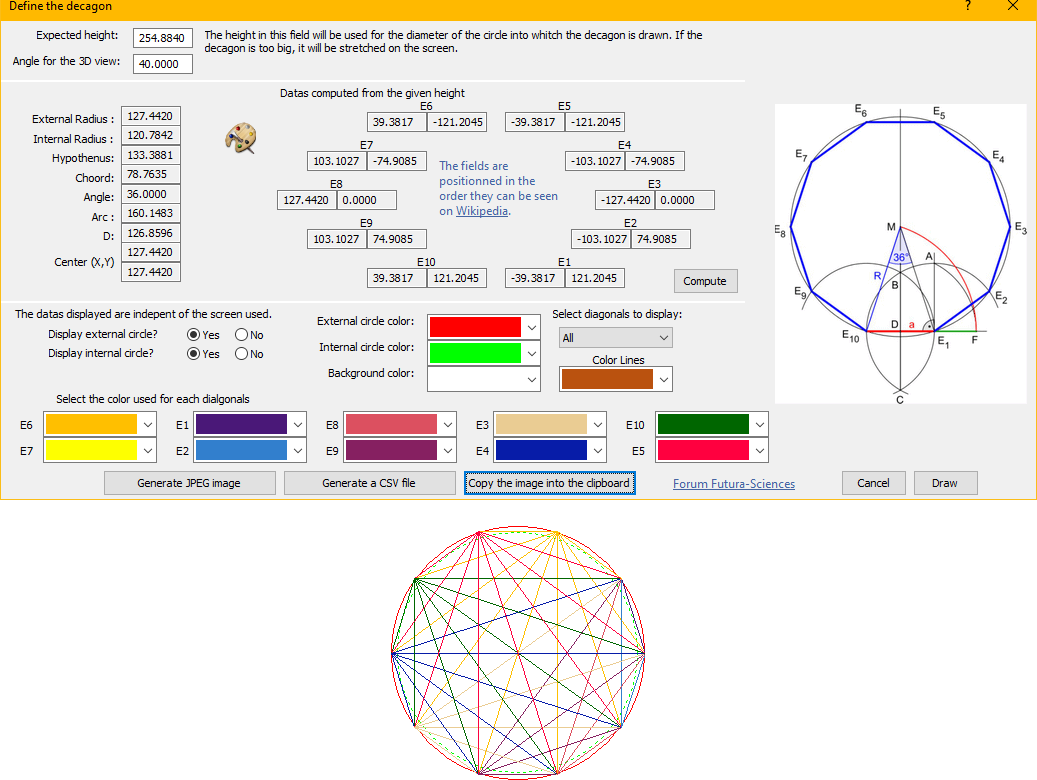
J'ai besoin de tracer un decagon régulier (10 côtés)
Chacun de ses côtés a un angle de 36°
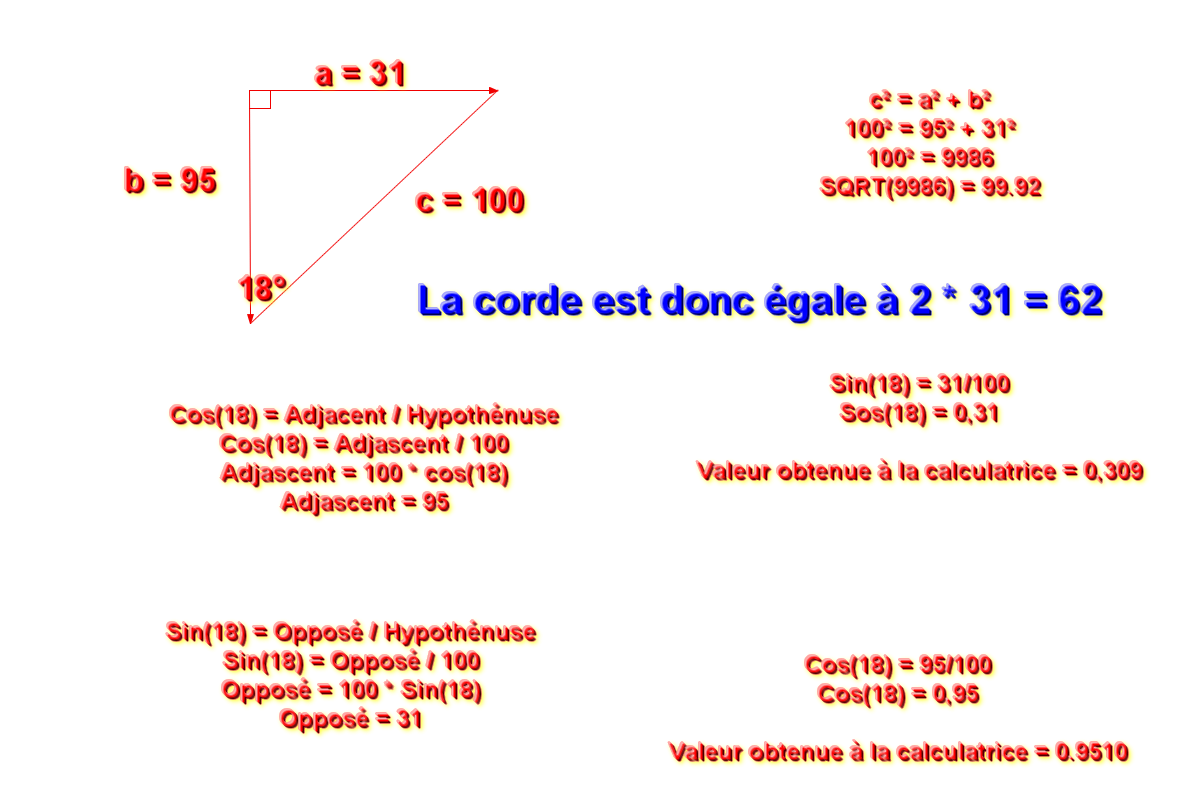
Chaque segment aura une longueur de 72.6
Comment vérifier que les 10 côtés de 72.6 rentre bien dans le cercle de rayon 100 ?
Sachant que :
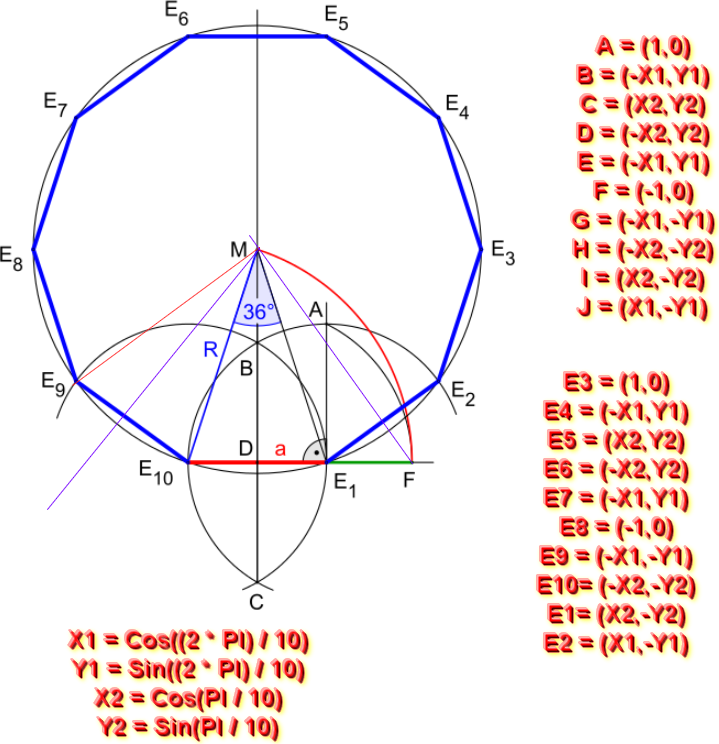
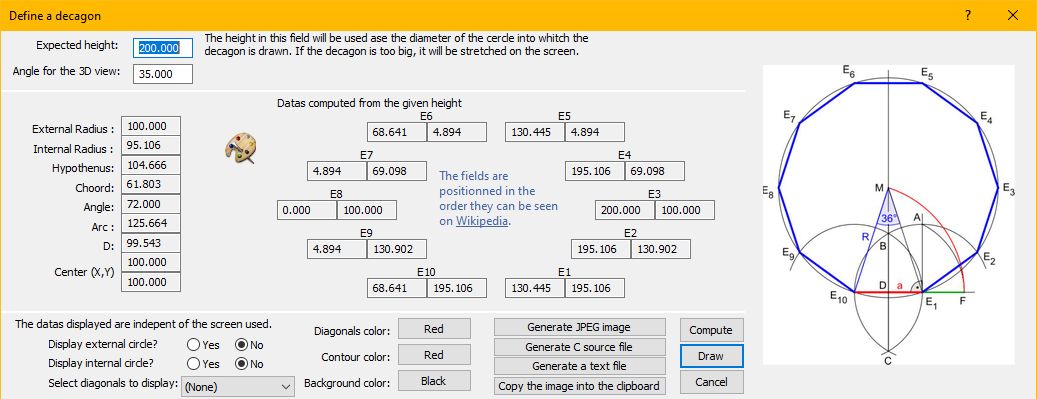
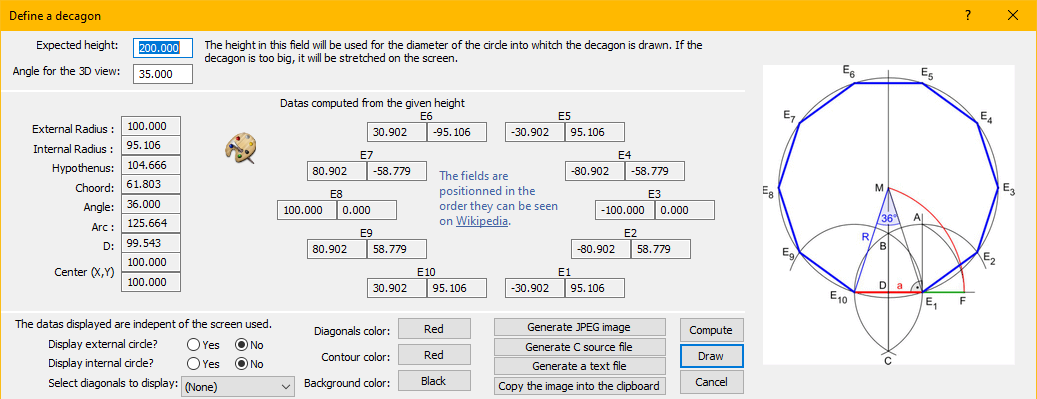
Je trace un cercle de rayon R = 100
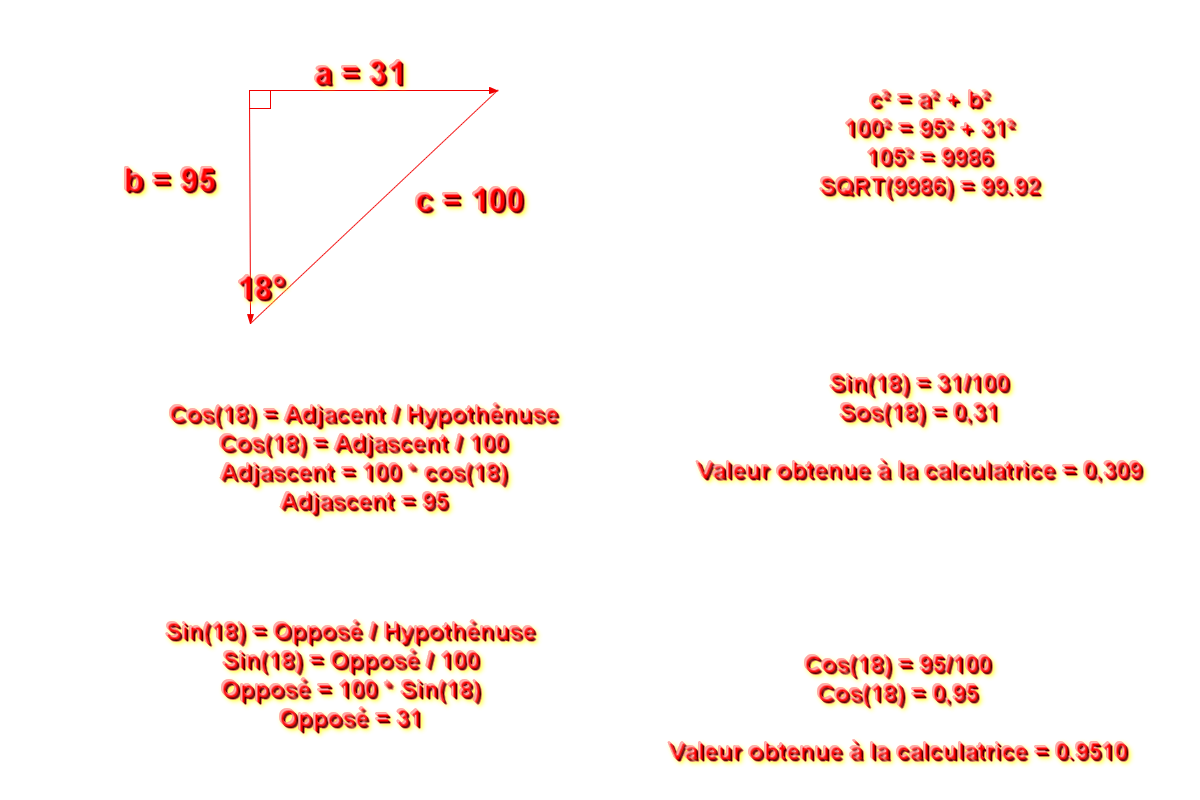
Dans ce cercle je positionne un triangle rectangle.
Ce triangle forme un angle de 54 degrés avec le centre du cercle.
En appliquant la loi des sinus, j'obtiens :
a = 72.6
+---------+
|C|.....B/
|-+...../
|....../
|...../ c = 123.6
b = 100 |..../
|.../
|../
|A/
|/
+
Angle de A = 36°
Angle de B = 54°
Angle de C = 90°
La somme des angle valant 180° : 90 - 54° - 36° = 180°
Sachant que b = R = 100
La longueur 'c' est égale (b / sin(B)) = c / sin(C))
Sinus(54°) = 0.8090169943749474241022934171 8282
Sinus(90°) = 1
(100 / sin(B)) = (c / sin(90))
(100 / 0.809) = (c / 1)
100 / 0.809 = c
c = 123.6
La longueur de 'a' peut alors être calculée :
Sinus(36°) = 0.5877852522924731291687059546 3907
(a / sin(A)) = 123.6
(a / sin(36)) = 1236.6
a / 0.587 = 123.6
a = 123.6 * 0.587
a = 72.6
Merci d'avance pour l'aide.
-----
