Primalité ou pas

[Porte7]

Bonjour,
Après avoir essayé un programme que j’ai écrit en c je me suis demandé si on pouvait avancer la chose suivante.
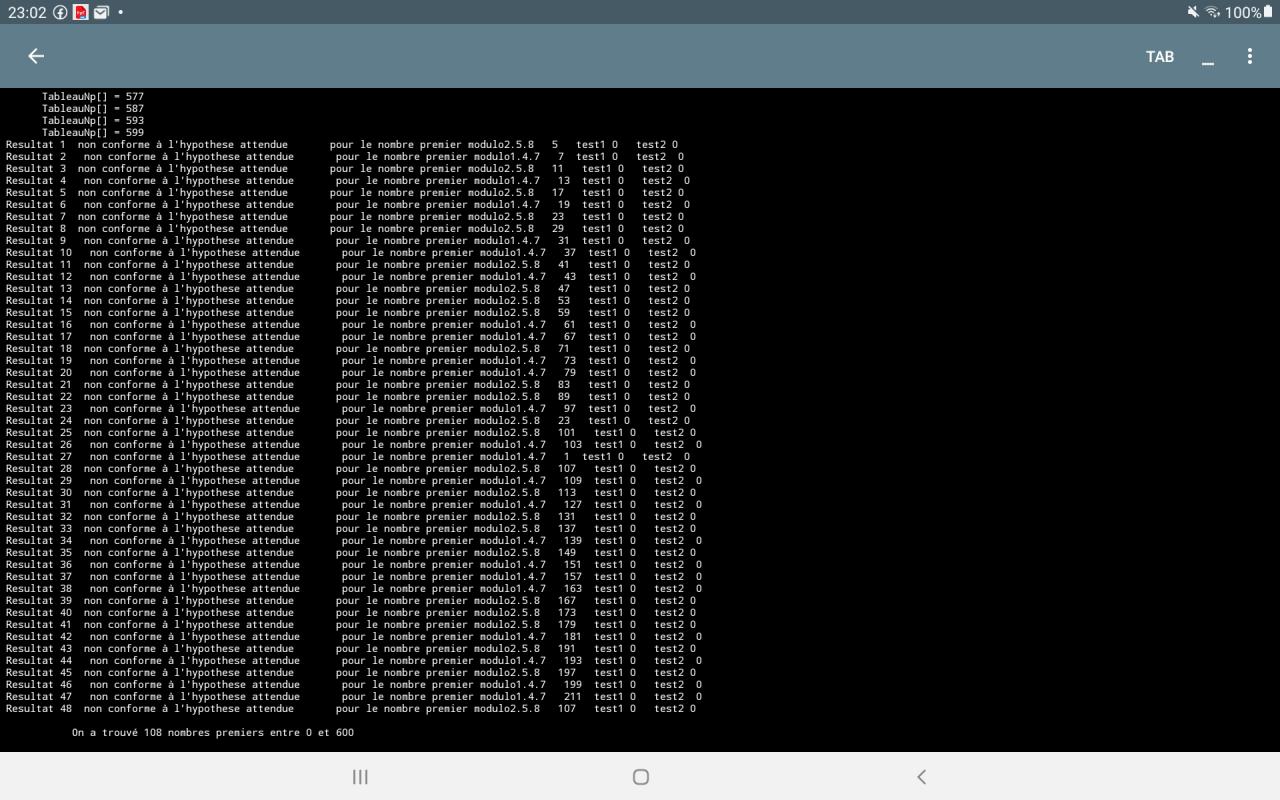
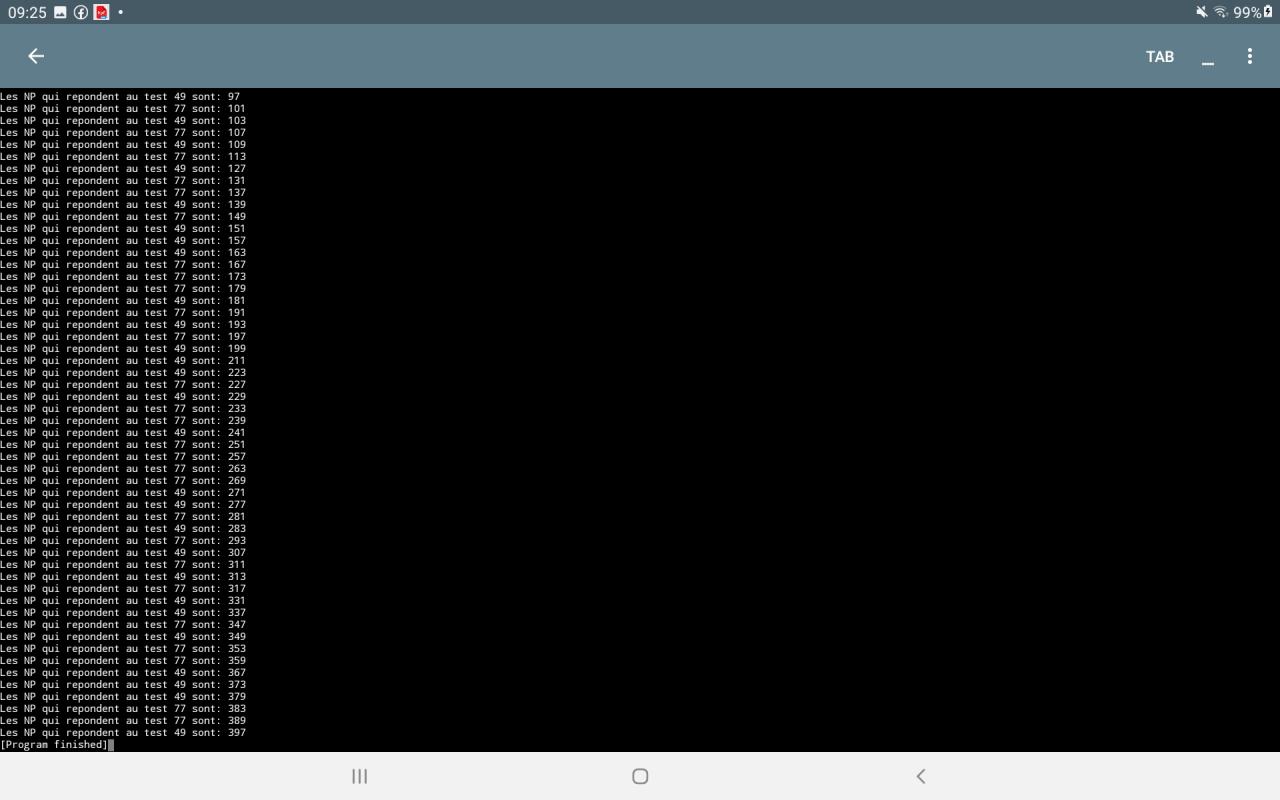
Tous les nombres non premiers dont la concaténation de chaine donne 1 4 ou 7 doivent satisfaire à l’une des 2 formules :
(X - 49)÷6 ou bien (X - 121) ÷ 6 = un nombre entier
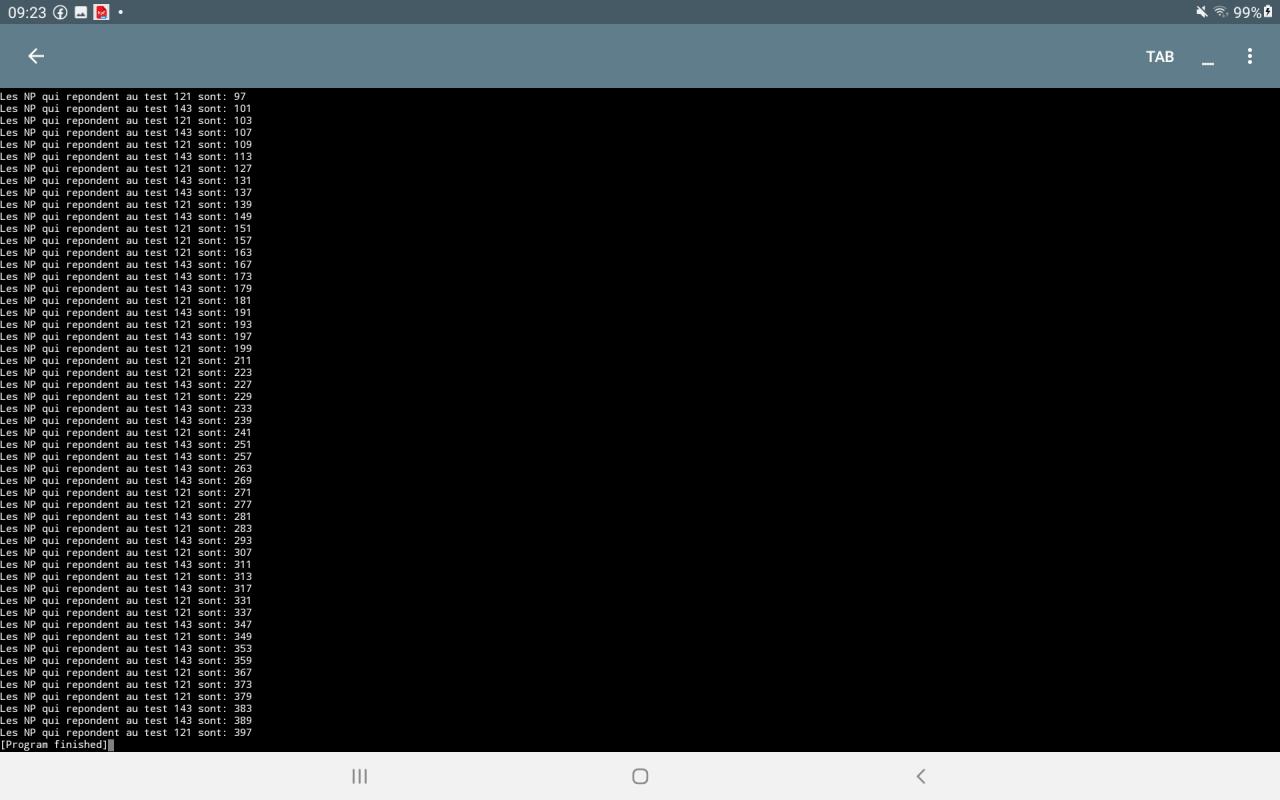
Pour ceux dont la concaténation de chaîne donne 2 5 ou 8 ils doivent satisfaire à l’une des 2 autres formules :
(X- 141) ÷6 ou bien (X - 77)÷6 = un nombre entier
Les nombres dont la concaténation de chaîne donne 3 6 ou 9 sont divisibles par 3
Pour ceux se terminant par 5 ou 0 j’en parle même pas.
Demain c’est le 11 septembre et c’est mon anniversaire, soyez indulgent svp merci.
-----

[Liet Kynes]

Bonjour,

l'idée c'est faire la somme des chiffres qui composent le nombre répétée jusqu'à obtenir un chiffre ?

Par exemple 95 -> 9+5=14->1+4=5 et ensuite 95-77=18 et 18/6=3 qui est un entier

[Porte7]

Voui monsieur pour la concaténation.
Mais suivant le résultat on appliquera les formules requises.

[Porte7]

Voilà le programme en c:

#include<stdio.h>
#include <stdlib.h>
#include <math.h>
#include<conio.h>
#include <time.h>


int main(int argc, char *argv[])
{

int a = 0;
int b =0;
int c =0;
int d =0;
int k =0;
int f =0;
int g =0;
int h =0;
int i =0;
int p = 0;
int NP=0 ;
printf(" Saisir jusqu’à quelle valeur vous voulez rechercher les nombres Impairs Non Premiers et Premiers : \n\n\n ");
scanf(" %d",&NP);
time_t begin = time(NULL);
int Tableau[NP] ;
for (int x=0; x<= NP; x++)
{
Tableau[x] = 0;
}

int sauvegarde =0;
int val1 =0;
int val2 = 0;
int val3 = 0;
int val4 = 0;
int val5 = 0;
int val6 =0;

suite1 :
b = 0;
while (NP>= (6*a+ 7) * (6*a + 6*b + 7 ))
{
printf (" %d ", (6*a+ 7) * (6*a + 6*b + 7 ));
val1 = (6*a + 7) * (6*a + 6*b + 7 );

Tableau[val1] = val1;
b++;
sauvegarde = b;
}
a++;
sauvegarde = sauvegarde -1;
if (sauvegarde >= 0)
{
goto suite1 ;
}
else
{
printf("\n\n\n");
goto suite2;
}
suite2:

g = 0;
while (NP>= (6*f + 11) * (6*f + 6*g + 11 ))
{
printf (" %d ", (6*f + 11) * (6*f + 6*g + 11 ));
val4 = (6*f + 11) * (6*f + 6*g + 11 );
Tableau[val4] = val4;
g++;
sauvegarde = g;
}
f++;
sauvegarde = sauvegarde -1;
if (sauvegarde >= 0)
{
goto suite2;
}
else
{
printf("\n\n\n");
goto suite3;
}

suite3:

k=2;
while (NP>= 3*k )
{
printf (" %d ", 3*k);
val3 = 3*k ;
Tableau[val3] = val3 ;
k++;
}
printf("\n\n\n");

k=2;
while (NP>= 5*k )
{
printf (" %d ", 5*k);
val6 = 5*k ;
Tableau[val6] = val6 ;
k++;
}
printf("\n\n\n");

suite4:

d = 0;
while (NP>= (6*c + 7) * (6*c + 6*d + 11 ))
{
printf (" %d ", (6*c + 7) * (6*c + 6*d + 11 ));

val2 = (6*c + 7) * (6*c + 6*d + 11 );
Tableau[val2] = val2;
d++;
sauvegarde = d;
}
c++;
sauvegarde = sauvegarde -1;
if (sauvegarde >= 0)
{
goto suite4;
}
else
{
printf("\n\n\n");
goto suite5;
}

suite5:

i = 0;
while (NP>= (6*h + 11) * (6*h + 6*i + 13 ))
{
printf ("\n %d ", (6*h + 11) * (6*h + 6*i + 13 ));

val5 = (6*h + 11) * (6*h + 6*i + 13 );
Tableau[val5] = val5;
i++;
sauvegarde = i;
}
h++;
sauvegarde = sauvegarde -1;
if (sauvegarde >= 0)
{
goto suite5;
}

printf("\n\n\n LISTE DES NOMBRES PREMIERS : \n");

int np_oupas;
int compteur = 0;

for (int z =3; z <= NP;z++ )
{

np_oupas = Tableau[z];
if (Tableau[z]== 0)
{
printf(" %d ", z);
compteur ++;

}
z++;


}

printf ("\n\n On a trouvé %d nombres premiers entre 0 et %d", compteur, NP);
time_t end = time(NULL);
printf("\n\n Le temps ecoulé pour une recherche sur %d nombres est de %d seconds", NP,(end - begin));

printf("\n\n\n");
}

Le programme peut être amélioré mais il me suffit.

[A voir en vidéo sur Futura]

[Liet Kynes]

Je crois que cela s'explique par l'arithmétique modulaire, les spécialistes vont te donner les détails.

[Porte7]

Exemple : 56 747 059 nombre premier
5+6+7+4+7+0+5+9= 43
4+3 =7
Test 56747059 -49 = 56747010 ÷ 6 = 9 457 835
mais 56747059 - 121 = 56 746 938 ÷ 6 = 9 457 823
C’est impossible qu’il apparaisse dans 2 boucles indépendantes.
Donc je pense que le Test n’est valable que si 1 seule condition est vérifiée et non les 2 en même temps.
Bonne journée à tous.

[gg0]

Bonjour Porte.

Le nombre que tu obtiens par "concaténation de chaîne" est simplement le reste de la division entiere de ton nombre par 9.
Je ne suis pas dans les conditions adéquates pour tester ta proposition, mais je la pense fausse, même si elle peut être vraie pour les entiers petits.

Cordialement.

[Porte7]

Vous devez avoir raison et j’en suis sûr.
Pour argumenter cette hypothese:

Je la tire du raisonnement suivant:

Des 6 boucles de recherche de tous les impairs non premier j’en ai 2 qui recherchent
les multiples de 3 et 5
Il me reste les autres boucles qui marchent sur des incrémenteurs i et j
Les voici:
(6*i + 11) * (6*i + 6*j + 11 )
(6*i + 7) * (6*i + 6*j + 7 )
(6*i + 11) * (6*i + 6*j + 13 )
(6*i + 7) * (6*i + 6*j + 11 )

On a donc à priori les résultats suivants:

X = (6*i + 11) * (6*i + 6*j + 11 )
X = 36i² + 66i + 36ij + 66j + 66i + 121
X = 36i² + 132i + 36ij + 66j + 121
X-121 = 6×(6i² + 22i + 6ij + 11j)
(X-121)/6 = 6i² + 22i + 6ij + 11j

X = (6*i + 7) * (6*i + 6*j + 7 )
X= 36i² + 42i + 36ij + 42j + 42i + 49
X-49 = 36i² + 84i + 36ij + 42j
X- 49 = 6× (6i² + 14i + 6ij + 7j)
(X-49)/6 = 6i² + 14i + 6ij + 7j



X = (6*i + 11) * (6*i + 6*j + 13 )
X = 36i² + 66i + 36ij + 66j + 78i + 143
..........(X-143)/6 = 6i² + 24i + 6ij + 11j


X = (6*i + 7) * (6*i + 6*j + 11 )
X = 36i² + 42i + 36ij + 42j + 66i + 77
(X-77)/6 = 6i² + 18i + 6ij + 7j

En résumé (X-121)/6 = 6i² + 22i + 6ij + 11j
(X-49)/6 = 6i² + 14i + 6ij + 7j
(X-143)/6 = 6i² + 24i + 6ij + 11j
(X-77)/6 = 6i² + 18i + 6ij + 7j
Pour chaque valeur X j’ai donc un couple (i,j) qui lui est propre et qui sont des entiers.
Le résultat des (X- [121,49,143,77])/6 est entier.
Le test de concaténation est issu d’une constatation sur les séries obtenues.
Pour la suite je m’en remet à vos avis éclairés.

[Porte7]

J’ai corrigé le programme et il semble bien que dans le cas d’un test non conforme attendu pour un nombre premier c-a-d quand le modulo 6 donne 0 le test est à 0 dans les 2 boucles testées ce qui n’est pas logique.
Donc une division par 6 qui donne 0 dans un test de nombre premier l’est dans 2 boucles à la fois.
J’ai l’impression que cela consolide mon hypothèse.
Ici le programme modifié :
#include<stdio.h>
#include <stdlib.h>
#include <math.h>
#include<conio.h>
#include <time.h>


int main(int argc, char *argv[])
{

int a = 0;
int b =0;
int c =0;
int d =0;
int k =0;
int f =0;
int g =0;
int h =0;
int i =0;
int p = 0;
int NP=0 ;
printf(" Saisir jusqu’à quelle valeur vous voulez rechercher les nombres Impairs Non Premiers et Premiers : \n\n\n ");
scanf(" %d",&NP);
time_t begin = time(NULL);
int Tableau[NP] ;
for (int x=0; x<= NP; x++)
{
Tableau[x] = 0;
}

int sauvegarde =0;
int val1 =0;
int val2 = 0;
int val3 = 0;
int val4 = 0;
int val5 = 0;
int val6 =0;

suite :
b = 0;
while (NP>= (6*a+ 7) * (6*a + 6*b + 7 ))
{
printf ("\n %d Vertical : %d Horizontal %d", (6*a+ 7) * (6*a + 6*b + 7 ),a,b);
val1 = (6*a + 7) * (6*a + 6*b + 7 );

Tableau[val1] = val1;
b++;
sauvegarde = b;
}
a++;
sauvegarde = sauvegarde -1;
if (sauvegarde >= 0)
{
goto suite ;
}
else
{
printf("\n\n\n");
goto suite2;
}
suite2:

d = 0;
while (NP>= (6*c + 7) * (6*c + 6*d + 11 ))
{
printf ("\n %d Vertical : %d Horizontal %d", (6*c + 7) * (6*c + 6*d + 11 ),c,d);

val2 = (6*c + 7) * (6*c + 6*d + 11 );
Tableau[val2] = val2;
d++;
sauvegarde = d;
}
c++;
sauvegarde = sauvegarde -1;
if (sauvegarde >= 0)
{
goto suite2;
}
else
{
printf("\n\n\n");
goto suite3;
}
suite3:


k=2;
while (NP>= 3*k )
{
printf ("\n %d Horizontal : %d", 3*k, k);
val3 = 3*k ;
Tableau[val3] = val3 ;
k++;
}
printf("\n\n\n");

k=2;
while (NP>= 5*k )
{
printf ("\n %d Horizontal : %d", 5*k,k);
val6 = 5*k ;
Tableau[val6] = val6 ;
k++;
}
printf("\n\n\n");


suite4:

g = 0;
while (NP>= (6*f + 11) * (6*f + 6*g + 11 ))
{
printf ("\n %d Vertical : %d Horizontal : %d", (6*f + 11) * (6*f + 6*g + 11 ),f,g);
val4 = (6*f + 11) * (6*f + 6*g + 11 );
Tableau[val4] = val4;
g++;
sauvegarde = g;
}
f++;
sauvegarde = sauvegarde -1;
if (sauvegarde >= 0)
{
goto suite4;
}
else
{
printf("\n\n\n");
goto suite5;
}

suite5:

i = 0;
while (NP>= (6*h + 11) * (6*h + 6*i + 13 ))
{
printf ("\n %d Vertical : %d Horizontal : %d", (6*h + 11) * (6*h + 6*i + 13 ),h,i);

val5 = (6*h + 11) * (6*h + 6*i + 13 );
Tableau[val5] = val5;
i++;
sauvegarde = i;
}
h++;
sauvegarde = sauvegarde -1;
if (sauvegarde >= 0)
{
goto suite5;
}

printf("\n\n\n LISTE DES NOMBRES PREMIERS : \n");

int sauv = 0;
int np_oupas;
int compteur = 0;

for (int z =3; z <= NP;z=z+2 )
{

np_oupas = Tableau[z];
if (Tableau[z]== 0)
{
printf("\n %d compteur %d", z,compteur);
compteur ++;
sauv = compteur;

}

}
// printf(" \n affiche sauv %d", compteur);
// scanf("%d",&compteur);
int TableauNp[sauv];
for(int i= 1, z=3; i <= sauv, z<= NP; i++,z=z+2)
{
if (Tableau[z] == 0)
{
TableauNp[i] = z;
printf("\n TableauNp[] = %d ", TableauNp[i]);
}
}

// LECTURE DU TABLEAU DE NOMBRES PREMIERS ET TESTS POUR VOIR // SI LE RESULTAT DE LA DIVISION PAR 6 DONNE UN NOMBRE A // VIRGULE ....AUTRE DIT SI LE MODULO 6 EST DIFFERENT DE 0.
int test;
int test1;
int test2;
int nombre;
int nbnonconforme =0;
// int sauvnombre;
for (int i = 1; i<= sauv; i++)
{
test = TableauNp[i];
// printf("\n Entrez le nombre premier à tester : ");
// scanf("%d",&test);
if (test%9 ==1 or test%9 == 4 or test%9 == 7)
{
test1 = test - 49;
test1 = test1 % 6;
test2 = test - 121;
test2 = test2 %6;
if ( test1== 0 or test2==0 )
{
nbnonconforme++;
printf("\n Resultat %d non conforme à l’hypothese attendue pour le nombre premier modulo1.4.7 %d test1 %d test2 %d",nbnonconforme, test,test1,test2);
}
}

if (test%9 ==2 or test%9 == 5 or test%9 == 8)
{
test1 = test - 143;
test1 = test1 % 6;
test2 = test - 77;
test2 = test2 %6;
if ( test1== 0 or test2==0 )
{
nbnonconforme++;
printf(" \n Resultat %d non conforme à l’hypothese attendue pour le nombre premier modulo2.5.8 %d test1 %d test2 %d",nbnonconforme,test,test1,t est2);
}
}
}
printf ("\n\n On a trouvé %d nombres premiers entre 0 et %d", compteur, NP);
time_t end = time(NULL);
printf("\n\n Le temps ecoulé pour une recherche sur %d nombres est de %d seconds", NP,(end - begin));
printf("TableauNp indice 105 valeur attendue %d", TableauNp[0]);

printf("\n\n\n");
}

[Porte7]

Capture sur ecran

[Liet Kynes]

Je n'y connais rien en code, peux tu expliquer plus précisément comment tu définis les "incrémenteurs" i et j ?

[Porte7]

Je suis pas fortiche car j’ai pas mal oublié.
Quand tu veux faire une multiplication en programmation
Tu poses déjà une boucle qui te permet d’exécuter des lignes de programme
Et les lisant comme un livre.
Les incrementeurs de boucle sont des variables qui sont modifiées à chaque portion de code ce sera ici
La variable i ( j’aurais lui donner le nom que je veux)
En C pour faire une multiplication
On peut poser ceci
1 Int nombre = 3;
2 for ( int i = 1; i <= 10 ; i = i + 1)
3 {
4 nombre = nombre × i ;
5 }
Explications:
Ligne 1 par int je définis le type de la variable ici un nombre entier
par nombre je donne un 'emplacement mémoire' ou 'variable' qui porte le nom que je choisis à ma convenance pour y loger la valeur 3 avec le signe = qui en informatique est une affectation d’une valeur à une
variable et non un signe d’égalité
Ligne 2 en français je dis
pour (la valeur de la variable i de type entière je lui affecte au depart la valeur 1;
Je teste la condition tant que i est inférieur ou égal à 10; et si le test est vrai alors j’incrémente de 1
la valeur de i ce qui donne2)
Ligne 3 je rentre par l’accolade ouvrante dans ĺa serie d’instructions qui seront réalisées ligne après Ligne Ligne 4 Ici j’en ai qu’une : je réalise l’opération de droite et je l’affecte à la variable ou emplacement
mémoire nombre
Soit nombre = 3×1;
Ligne 5 arrivé devant l’accolade fermante je remonte dans le for pour réaliser le test i<= 10 et comme le
test est vrai je réalise la dernière instruction du for c à d i = i + 1
Je repart ainsi dans la série d’instruction entre {}
La valeur de nombre est 3
La valeur de i est 2
J’affecte 3×2 à nombre qui porte maintenant la valeur 6
Quand i vaudra 10 nombre passera à 30
Et quand i vaudra 11 je sortirai de la boucle for et ma table de multiplication s’arrêtera à 30.
Cdlt

[Liet Kynes]

Le fonctionnement du code ne m'intéresse pas, ce que je veux comprendre c'est ce que tu fais d'un point de vue calcul.
Ce que tu décris au départ comme démarche concernait des nombres non premiers.

[Porte7]

J’ai utilisé les fonctions de recherche de tous les multiples que j’ai donné dans le post #8.
Elles donnent tous les nombres composés entre 0 et.........100000000
Elles sont à 2 inconnues i et j.
A partir de là avec une cuisine informatique on a les nbs premiers de 0 à 100000000 par exemple.
Donc tous les multiples sont égaux à une des 6 fonctions.
Cdlt

[Liet Kynes]

Ce ne sont pas les sommes des chiffres qui composent un impair non premier que tu testes ? Si oui je ne comprends plus l'hypothèse de départ.

[Porte7]

Tiens voilà Liet voilà ma logique algorithme pour sortir tous les multiples des nombres.
C’est une table de multiplication.
Un schéma est plus facile à comprendre.
Pour l’hypothèse elle s’est avérée pipo.
Désolé
Reste un algorithme qui permet de trouver en poursuivant la programmation tous les nombres premiers
En dessous de n = 100 millions en un peu plus de 22 mn.
Bonne journée.

[Porte7]

Liet tu as raison j’ai ensuite fait le modulo de tous les multiples impairs trouvés et j’en ai déduit faussement l’hypothèse que j’ai faite par extension aux nombres premiers.
Cela a été vérifié hier par programmation.
Je fais une photo dans 5 mn...

[Porte7]

Voilà mes tests d’hier Liet
Cdlt

[Porte7]

Et suivant

Cdlt
(Absent aujourd'hui)

[Liet Kynes]

En fait tu crées un programme de calcul des nombres premiers ?
Sur ce site il y a des listes générées : http://nombrespremiersliste.free.fr/

Et le programme est en partage :

http://nombrespremiersliste.free.fr/....cpp.view.html
http://nombrespremiersliste.free.fr/#pgr
Je ne sais pas si il y a un moyen de tester la fiabilité de ce type de programme pour les utilisateurs non-programmeurs, peut-être que des listes "officielles" existent ?

[Porte7]

Rebonjour
Ce travail mériterait d’être vérifié, mais en première approche

Les 2 premières fonctions A et B donnent TOUS LES NOMBRES PREMIERS avec TOUS leurs multiples
A = (6*i +1)
B = (6*i +5)
A vérifier.
Pour les fonctions suivantes j’en suis sûr:
Les 4 fonctions suivantes C , D ,E , F donnent TOUS LEURS MULTIPLES sans les nombres premiers !!

C= (6*i + 11) * (6*i + 6*j + 11 )
D=(6*i + 7) * (6*i + 6*j + 7 )
E=(6*i + 11) * (6*i + 6*j + 13 )
F=(6*i + 7) * (6*i + 6*j + 11 )

Je me demande ce que fait ({A }+ {B}) - ({C} + {D} + {E} + {F}) ?????
Il restera malgré tout dans une certaine mesure les multiples de 2 3 et 5 mais ça je crois qu’on en crèvera pas!!!
On pourra rajouter 1 2 et 3 même si 1 n’est pas premier.
Merci.

[gg0]

Bonjour.

Tu te satisfais de peu ! Rien à voir avec les maths.
Et tu dates un peu, ça fait plus de 2300 ans qu'on sait que en dehors de 2 et 3, tous les nombres premiers sont de la forme 6k+/- 1.
Je passe sur la suite, mélange d'évidences et d'erreurs.
On connaît beaucoup de choses sur les nombres premiers, apprends les bases de l'arithmétique.

Cordialement.

[Porte7]

Bonjour,
Oui très certainement.
Mais bon on peut arriver à trouver un certain plaisir aussi à découvrir ces choses là par soi même et à faire un programme informatique pour passer son temps libre.
Cdlt

[pm42]

Mais bon on peut arriver à trouver un certain plaisir aussi à découvrir ces choses là par soi même et à faire un programme informatique pour passer son temps libre.

En effet. Sauf que tu demandes aussi aux membres du forum de passer du temps à vérifier que tu as bien redécouvert l'eau tiède, le tout en lisant un long code sans avoir mis les bonnes balises autour pour le rendre lisible.
Donc cela peut faire baisser l'indulgence.

[gg0]

On n'est pas obligé de venir sur un forum annoncer qu'on a inventé l'eau tiède ��
Cordialement.

[Liet Kynes]

On n'est pas obligé de venir sur un forum annoncer qu'on a inventé l'eau tiède 😉
Cordialement.

Inventer l'eau tiède est le contraire de ne pas avoir inventer l'eau tiède: https://fr.wiktionary.org/wiki/ne_pa...eau_ti%C3%A8de
Partager cette invention sur un forum "gratuitement" est généreux.

[Porte7]

Merci Liet

[Liet Kynes]

Merci Liet

Généreux prends un sens double: pour celui qui "redécouvre" c'est une bonne intention, pour celui à qui sont offertes ces "re-découvertes" trop régulièrement cela alimente généreusement une forme de lassitude.
C'est un problème dans les forums ou des questions reviennent continuellement, souvent quelqu'un renvoie vers une discussion qui fait référence pour ne pas éternellement recommencer le même débat.
Par exemple un des grand classique des forums Math est régulièrement ré expliqué en utilisant ce post: https://forums.futura-sciences.com/m...nir-0-0-a.html