Bonjour,
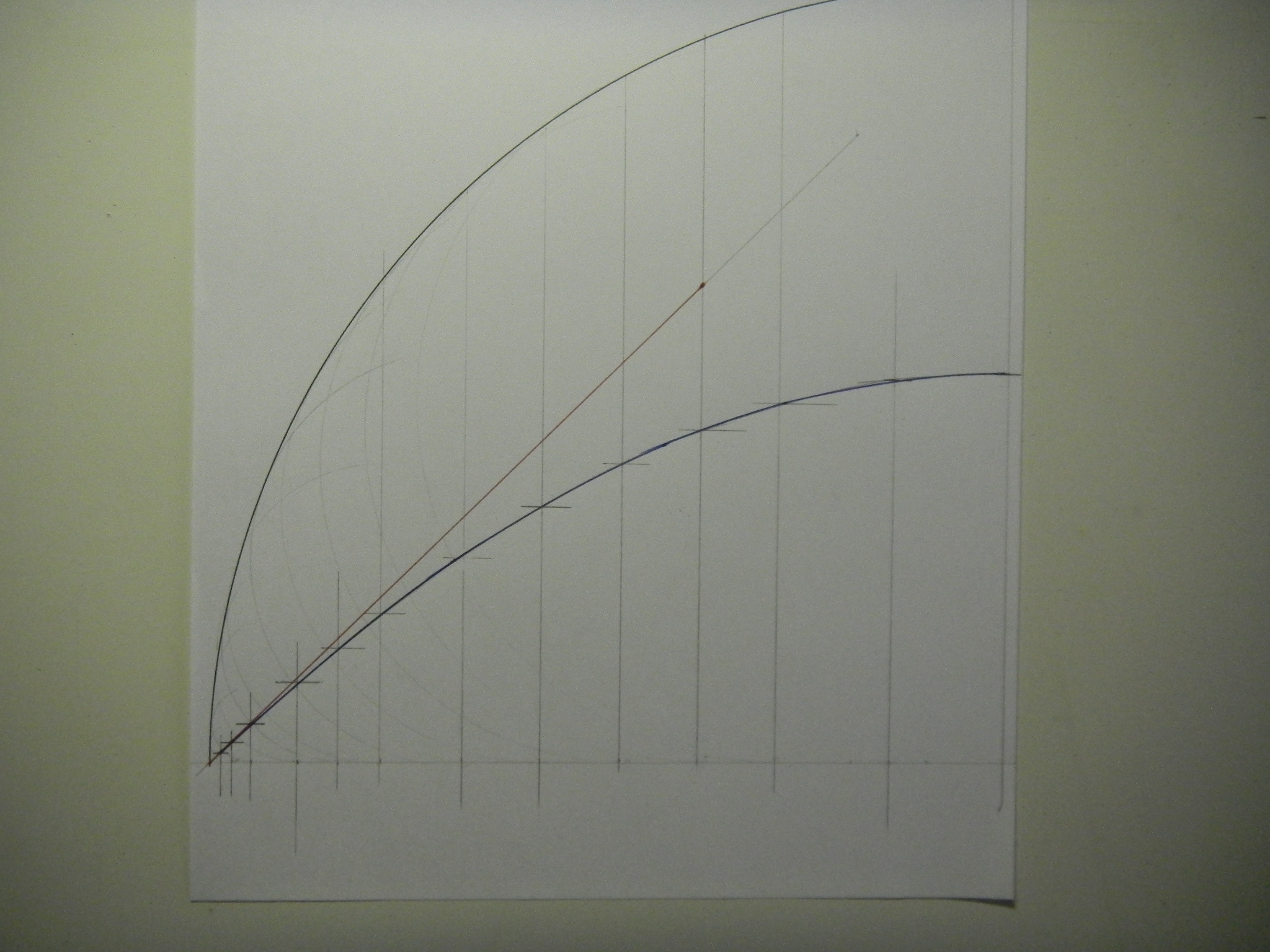
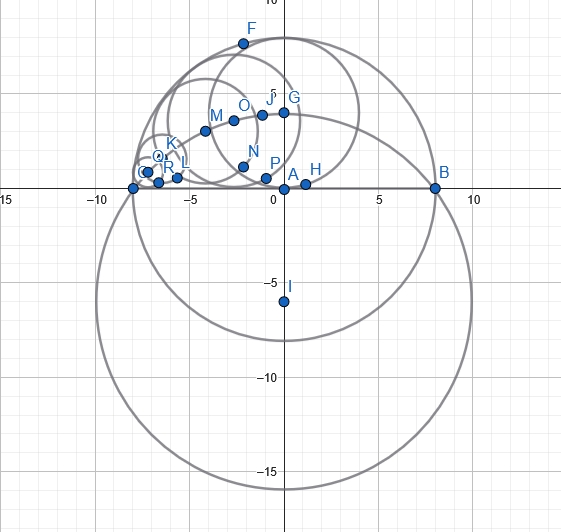
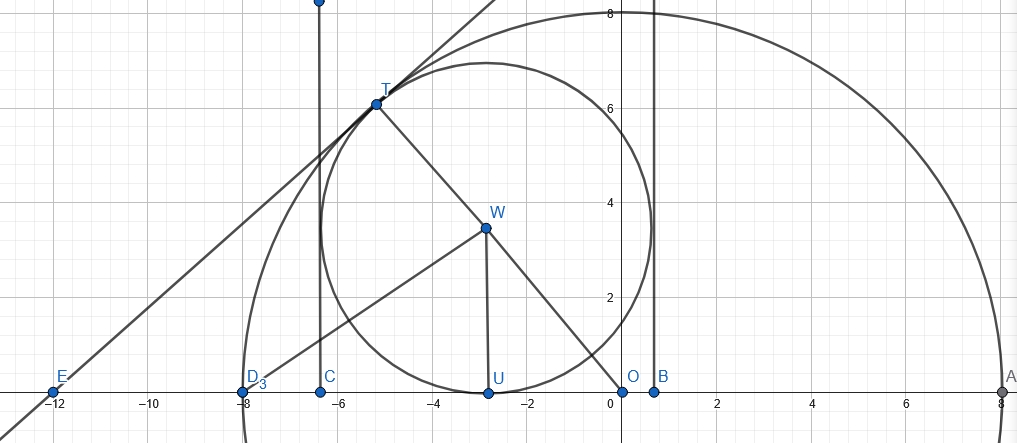
Je ne réussis pas du tout à résoudre ce problème où un cercle (de centre W) est inscrit dans un demi-cercle (de centre O), tangent à la fois à un diamètre AD (en U), au demi cercle (en T), et à deux perpendiculaires à ce diamètre dont les points de projection sont B et C.
Je dois démontrer que BC^2 = 4 AB x CD
(En pratique, si on me donne juste AB et CD, je dois pouvoir en déduire BC (et donc le diamètre du demi-cercle et celui du cercle inscrit, ce qui est immédiat).
Je ne vois carrément pas comment procéder. Merci de votre aide.
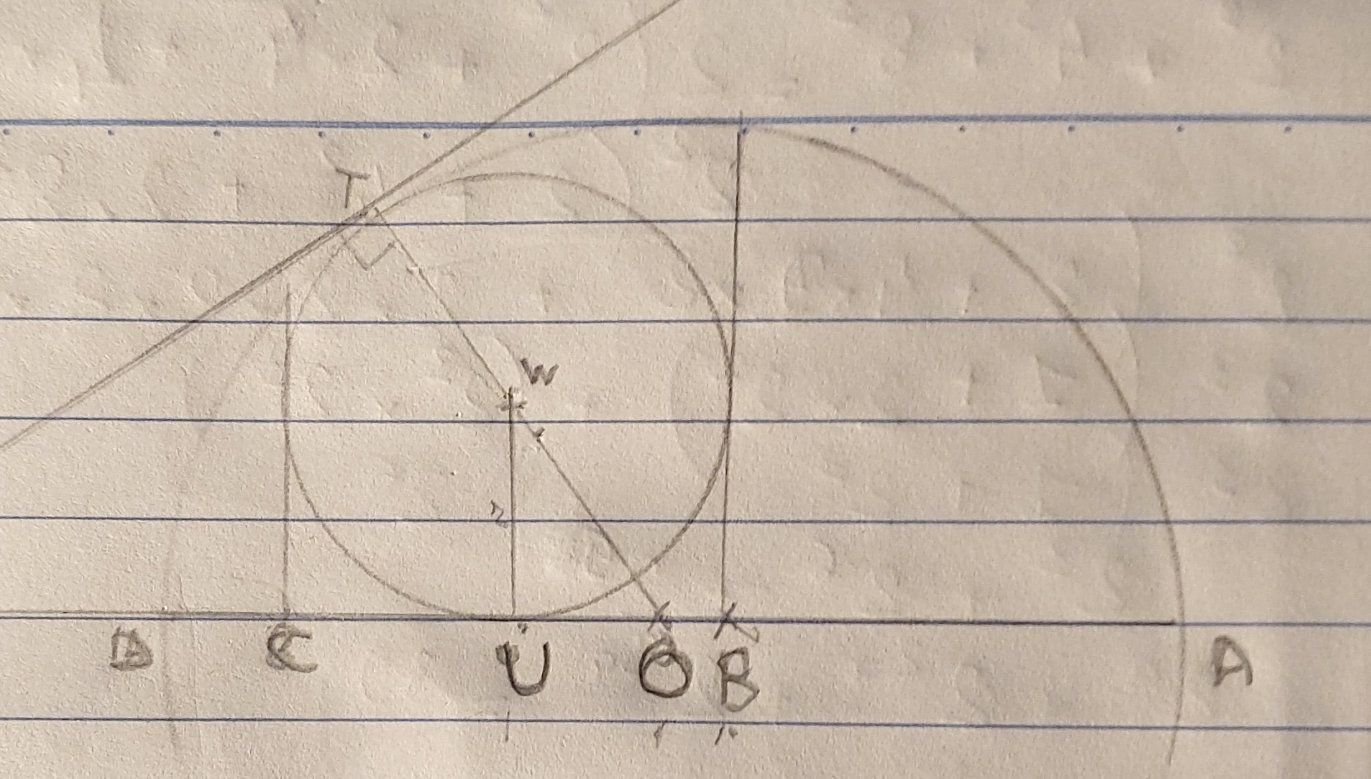
-----




 et
et