Fonction exponentielle

[invite43219988]

Bonjour,
j'aimerai savoir si vous savez comment on a pu trouver avec certitude la fonction exponentielle. En fait, m'expliquer pourquoi
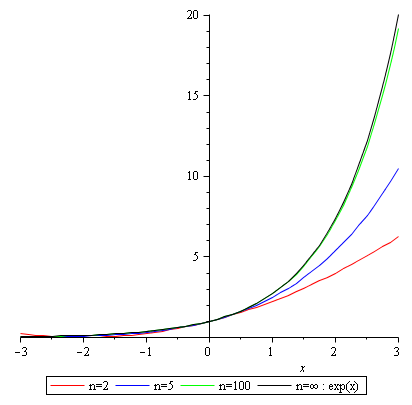
exp(x)=2.71828...^x
On sait que cette fonction doit être égale à sa dérivée mais je ne vois pas comment trouver le nombre e.
Je voulais aussi savoir si la fonction ln(x) applique un calcul connu à x où si on a simplement déterminé par où cette fonction devait passer pour respecter ln(xy)=ln(x)*ln(y)

[Gaétan]

ln(xy) = ln(x) + ln(y)

[Paul_UTT]

Oupss trop tard, Gaétan a déjà rectifié.

[invite43219988]

lol désolé je n'ai pas fait attention

[Jeanpaul]

Sachant que e^x est sa propre dérivée, on peut en appliquant la formule de Taylor au voisinage de 0 faire un développement limité (très simple et très classique) de e^x.
Si on fait dans ce développement x=1, on va trouver e^1 = e = 2.718281828...

[Marc]

Sachant que e^x est sa propre dérivée, on peut en appliquant la formule de Taylor au voisinage de 0 faire un développement limité (très simple et très classique) de e^x.
Si on fait dans ce développement x=1, on va trouver e^1 = e = 2.718281828...

Je ne vois pas comment ça te permet de définir le nombre e ...
Par contre, une définition consisterait à dire que c'est la limite de la somme des 1/k! . Ainsi, en sommant beaucoup de termes, j'imagine qu'on a pu approcher sa valeur.

Marc

[gilllloux]

Par definition :

e^x = x^0 / 0! + x^1 / 1! + x^2 / 2! + ...

En particulier :

e = e^1 = 1/0! + 1/1! + 1/2! + 1/3! + ...

[invite43219988]

e^x = x^0 / 0! + x^1 / 1! + x^2 / 2! + ...

J'aimerai savoir à quel niveau d'étude on voit cette définition et ensuite, pourquoi e^x peut se développer de la sorte.
Par exemple, pour déterminer pi, sachant que ce nombre est la moitié du périmètre d'un cercle de rayon 1 (ou le rapport entre le périmètre et le diamètre), on peut l'approcher en dessinant des triangles isocèles dans une partie de ce cercle (partie délimitée par l'arc de cercle et le diamètre). On obtient ainsi une suite qui tend vers pi mais cette suite, on sait d'où elle vient.
e je ne sais pas du tout ce qu c'est et à quoi ca correspond donc j'aimerai comprendre ta formule.

[Gaétan]

Ce que tu dis avec les triangles et le nombre pi est, disons, une "monstration" géométrique. Mais avec un dévellopement de Taylor, tu peux le démontrer analytiquement comme pour e. Ce qu'il faut démontrer, c'est la formule du dévellopement de Taylor (j'ai vu ça en prmière cndi, si je me souviens bien). Le reste, les formules pour pi et e, c'est juste de l'application de formule (que je ne connais pas par coeur).

[invite43219988]

Quelqu'un pourrait me faire une vulgarisation du développement de Taylor svp ?

[doryphore]

Je peux déjà te dire que les développements en séries de Taylor viennent de la volonté d'approcher (et non pas approximer) des fonctions suffisamment régulières pas des polynomes.

On peut voir une série de Taylor comme une "suite-somme" (c'est ce qu'on appelle série) de polynômes qui converge vers la fonction étudiée.

Il est alors important d'évaluer le reste (i.e. la différence entre la série de polynôme (ou sa valeur en un point) et la fonction étudiée (ou sa valeur en un point). Il y a plusieurs manières d'évaluer ce reste et l'important est de trouver la bonne.

Pour la fonction exponentielle, on a de la chance, la fonction exponentielle est analytique donc est égale à sa série de Taylor.

[invite43219988]

Merci pour ce début d'explication

[Quinto]

C'est beaucoup plus qu'un début d'explication, tu viens de te voir résumer 3ans de cours d'analyse dans cette jolie explication de doryphore...
C'est peut etre bete à dire mais e^x=exp(x).
Ca ne parrait etre qu'une notation, mais en fait pas du tout, et e n'est pas choisi au hasard, c'est la limite de la suite u(n)=(1+1/n)^n.

En fait de part les propriétés de exp et de ln, on a que ln(e)=1 et ln(x^y)=yln(x) sur R*+, donc en particulier ln(e^x)=xln(e)=x et de même ln(exp(x))=x par définition d'une application réciproque.
Ainsi on a par bijectivité (unicité) que exp(x)=e^x.
Ensuite pour évaluer une valeur approchée de e, on a plusieurs méthodes, telle la dichotomie par exemple, qui est une méthode assez simple et assez bonne.
Sinon la méthode qui utilise le développement de Taylor, mais là comme tu as vue, il faut avoir des notions d'analyse un peu plus poussées pour savoir pourquoi ca marche, mais c'est assez rapide cependant:
1+1+1/2+1/6+1/24=2.7083333....
1+1+1/2+1/6+1/24+1/120=2.7166666....
1+1+1/2+1/6+1/24+1/120+1/720=2.718055556....

Tu vois qu'à un ordre 6 on arrive déjà "pratiquement" au nombre e, en fait on a déjà 4 décimales qui sont exactes...
à l'ordre 9, on en a 6 qui sont exactes, etc..

[invite43219988]

Comment utiliser la dichotomie pour trouver e ?
Sur quelle fonction dois je l'utiliser ?

En utilisant ln(e) = 1 non ?

[Quinto]

Tu peux l'utiliser sur n'importe quelle fonction qui te plait et qui fait intervenir e, mais la plus simple sera la meilleure.

la fonction
x->ln(x)-1 sur R*+ est je pense l'une des plus adaptée.