Bonjour,
dans le cadre d'un projet d'analyse numérique, on me demande un calcul de valeurs propres et de vecteurs propres.
On étudie tout d'abord une matrice tridiagonale T de taille n*n telle que:
j'ai trouvé que les valeurs propres valaient
et les vecteurs propres
On considère ensuite la matrice 2n*2n
R=(0 I)
__(T 0)
avec I la matrice identité de taille n*n et T la matrice définie précédemment. On doit calculer les valeurs et vecteurs propres de R. J'ai essayé mais j'aboutis à Lambda(valeur propre)=+-Racine(a) ce qui me semble incorrect.
Pourriez vous m'aider s'il vous plait? Je vous remercie d'avance.
Claire
-----




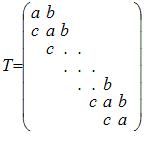
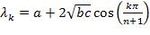
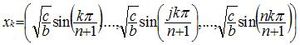


 est une colonne de taille
est une colonne de taille