Hyperbole et asymptote oblique.

[astropierre]

Bonjour

J'ai posté cette question sur le forum "Mathématique du Collège et du Lycée", mais je me demande si cela ne nécessite pas un niveau un peu plus élevé...
Je vous soumet donc mon souci dans ce que j'espère être le forum le plus adapté.


Voilà, je suis en thèse de Physique, un peu honteux d'avoir visiblement oublié quelques bases en maths.

Pour faire simple, mon problème se résume à ceci :

J'ai, dans un repère orthonormé, 2 droite D1 et D2 quelconques (non strictement verticales, on est en Physique, ça n'existe pas, chez nous, des phénomènes aux pentes infinies ^^) dont je connais l'équation.

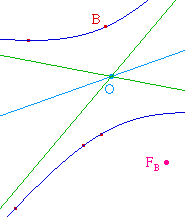
J'ai besoin de connaître l'équation ( y = f(x) ) de l'hyperbole qui se trouve en dessous de ces 2 droites, et qui possède D1 comme asymptote en -infini, et D2 comme asymptote en +infini
Je cherche l'équation de cette hyperbole en fonction des coef. directeurs et des ordonnées à l'origines de mes 2 droites.

Merci de votre aide

Pierre

[God's Breath]

Bonjour,

Les droites ont pour équations respectives et .
Une hyperbole admettant ces droites pour asymptotes aura pour équation (hyperbole rapportée à ses asymptotes, équation ...).
Le problème, c'est qu'il n'existe pas une seule hyperbole conforme à ta description ; il faudrait connaître, par exemple, un point de l'hyperbole afin de préciser la valeur de .

[astropierre]

Bonjour,

Les droites ont pour équations respectives et .
Une hyperbole admettant ces droites pour asymptotes aura pour équation (hyperbole rapportée à ses asymptotes, équation ...).
Le problème, c'est qu'il n'existe pas une seule hyperbole conforme à ta description ; il faudrait connaître, par exemple, un point de l'hyperbole afin de préciser la valeur de .

Merci, God's Breath, pour la célérité de ta réponse

Il me reste toutefois un petit problème :

L'ensemble des points qui obéissent à cette égalité forment, non pas une, mais deux hyperboles, ainsi que le montre la petite image ci-dessous.



mais chacune de ces deux hyperboles, prise individuellement, doit pouvoir être décrite par une équation du style


C'est l'équation de l'hyperbole du bas que je désire trouver et que j'ai quelques difficultés à avoir, vois-tu ?...

[God's Breath]

Bonjour,

Ton problème est un «faux» problème. L'équation représente les deux branches de l'hyperbole.
Dès qu'on a la valeur de , on développe l'équation, qui se trouve être du second degré en , , que l'on résout (j'ai la flemme de calculer le discriminant...).

La branche inférieure qui t'intéresse est donnée par , alors que la branche supérieure, qui ne t'intéresse pas, est donnée par a branche inférieure qui t'intéresse est donnée par .

Mon problème est plutôt de déterminer pour que l'hyperbole soit bien disposée comme tu le veux, plutôt que dans les deux autres secteurs limités par les droites.

[astropierre]

C'est pas faux...

Bon, en tout cas, merci beaucoup pour le coup de main. A partir de ça, je devrais pouvoir me débrouiller comme il faut.
^^