Segment sur courbe de bezier

[inviteba791690]

Hello,

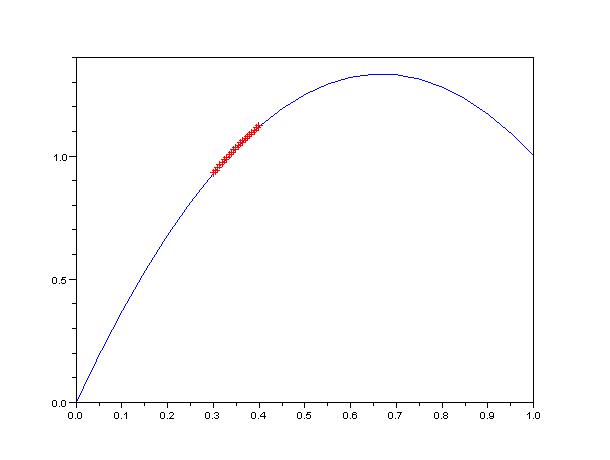
J'utilise une courbe de bezier avec 3 points (2 d'ancrages et un de contrôle).

Sur cette courbe j'ai 2 points qui forment un segments, j'aimerais pouvoir retrouver les coordonnées du point de contrôle à appliquer à ce segment afin que celui-ci épouse la forme de mon bezier.
Sachant que j'ai toutes les autres informations (coordonnées des points d'ancrages du segments et de la courbe ainsi que les coordonnées du point de contrôle de la courbe)

J'imagine qu'il y a certainement une formule pour ca mais comme je ne suis pas Einstein j'ai un peu de mal

Merci à celui qui pourra m'aider
-----

[KerLannais]

Salut,

C'est vrai que c'est une question intéressante Si j'ai bien compris, tu considère une courbe de Bézier à 3 points, notons A et B ses extrémités et C le point de contrôle. Alors la courbe est donnée par l'ensemble des points

pour (autrement dit M(t) est le barycentre des points pondérés , et . Tu considères un sous-arc définit à l'aide de deux points E et F pris sur la courbe et tu te pose la question de savoir si cette arc est encore une courbe de Bézier à 3 points d'extrémités E et F, en particulier tu veux savoir quel serait le point de contrôle G. J'ai supposé qu'on connaissait les coefficients et tels que et , dans ce cas le point est donné par:

(si je ne me suis pas trompé dans les calculs)
avec ce point de contrôle on a pour t entre et

avec (en supposant par exemple)

[inviteba791690]

Merci pour ta réponse.

J'avais je crois trouvé la solution puisque au final on est dans le cas d'une équation à une inconnu. En partant de la formule connu (sur celle ci on est d'accord ):


Soit comme tu l'as dit E et F les 2 ancres qui se trouve sur la courbe et G le point de contrôle à appliquer pour épouser la courbe d'origine.


Alors je te cache pas que même si j'aime les maths j'ai pas fais mathsup et que j'ai un peu du mal avec ces notations .
En partant de plus concret avec mon code ca donne pour la 1ére formule :

x = Ax * ( 1 - t )² + Cx * 2 * t * ( 1 - t ) + Bx * t²; (pour coordonées x d'un point de la courbe)
y = Ay * ( 1 - t )² + Cy * 2 * t * ( 1 - t ) + By * t²; (pour coordonées y d'un point de la courbe)

Avec un 0 < t < 1 je récupère tous les points de la courbe

En partant de l'équation que j'ai trouvé et qui n'a pas l'air de correspondre à la tienne ca donne en concret

Gx = ( px - ( 1 - t )² * Ex - t² * Fx ) / ( 2 * t * ( 1 - t ) );
Gy = ( py - ( 1 - t )² * Ey - t² * Fy ) / ( 2 * t * ( 1 - t ) );

ou px et py sont les coordonées de n'importe quel point de la courbe (qui sont récupérés avec la formule précédente) entre E et F mais pas E ou F.

Ta formule à l'air plus simple mais comme j'ai du mal avec les notations de maths je vois pas comment l'appliquer dans mon cas concret.

Si tu as des précisions depuis ta formule en partant de mon "plus concret" je suis preneur même si mon bousin à l'air de fonctionner je suis pas contre d'autres solutions.

Merci encore d'avoir répondu.

[KerLannais]

Re

La notation

signifie simplement



t_E et t_F sont tels que





Pour s parcourant [0,1], le point de coordonnées (x,y) définies par


parcourt l'arc d'extrémité E et F.

[A voir en vidéo sur Futura]

[inviteba791690]

Ok j'ai compris la notation t_E et t_F représentent simplement la valeur de t pour E et F sur la courbe ABC.

J'ai donc essayer d'appliquer ta formule pour Gx et Gy mais le résultat n'est pas correct même si je pense que cette formule n'est pas loin de la solution idéale, visuellement ca donne ca :
http://www.samystudio.net/DashedLine2.swf

alors qu'on devrait avoir ca :
http://www.samystudio.net/DashedLine1.swf

La ligne rouge correspond à l'ensemble ABC et les lignes noires à plusieurs ensembles EFG

[KerLannais]

Salut,

c'est étrange car quand je teste avec
Ax=0,Ay=0,Bx=1,By=1,Cx=0.5,Cy= 2,tE=0.3,tF=0.4
je trouve
Ex=0.3,Ey=0.93,Fx=0.4,Fy=1.12, Gx=0.35,Gy=1.04
et quand je trace j'obtient le graphe en pièce jointe



la courbe bleue est l'ensemble des points de coordonnées
x=(1-t)^2Ax+2t(1-t)Cx+t^2Bx
y=(1-t)^2Ay+2t(1-t)Cy+t^2By
pour t dans [0,1]

la courbe rouge est l'ensemble des points de coordonnées
x=(1-t)^2Ex+2t(1-t)Gx+t^2Fx
y=(1-t)^2Ey+2t(1-t)Gy+t^2Fy
pour t dans [0,1]

mais je veux bien tester avec les valeurs que tu as utilisé pour voir.

[inviteba791690]

Je ne comprend pas comment tu arrive à Gx=0.35

Si je suis la formule :

soit:
( 1 - .3 ) * ( 1 - .4 ) * 0 + ( .3 + .4 - 2 * .3 * .4 ) * 1 + .3 * .4 * .5
ca me donne Gx = .52

mais en tous cas si j'utilise les valeurs de Gx et Gy de ton exemple en effet ca marche.

Autre chose pour mon info perso comment es tu arrivé à la formule
?

Merci encore

[KerLannais]

Ca y est j'ai compris, mille excuses je me suis trompé la formule c'est



(j'avais inverser B et C je suis très étourdi)

Après, comment j'ai trouvé ça ... c'est juste du calcul mais c'est pénible à taper dans une réponse, mais je vais taper ça dans un fichier et je te l'envoie.

[inviteba791690]

Génial c'est ca

Le pire c'est que je me doutais d'un truc dans le genre et j'avais essayer d'inverser B et C mais j'avais du faire d'autres modifs en même temps et ca marchait pas.

un autre swf manipulable pour bien se rendre compte du bouzin :
http://www.samystudio.net/curveSegment.swf

Merci beaucoup

ps : je suis toujours preneurs de la méthodo pour arriver à cette formule

[KerLannais]

Voilà

J'ai fini de taper
Bezier.pdf
j'espère qu'il n'y a pas trop de coquilles et que l'orthographe n'est pas trop massacrée

[inviteba791690]

Merci je vais étudier ca histoire d'être moins con