exercice démonstration par récurrence

[invite630d42bb]

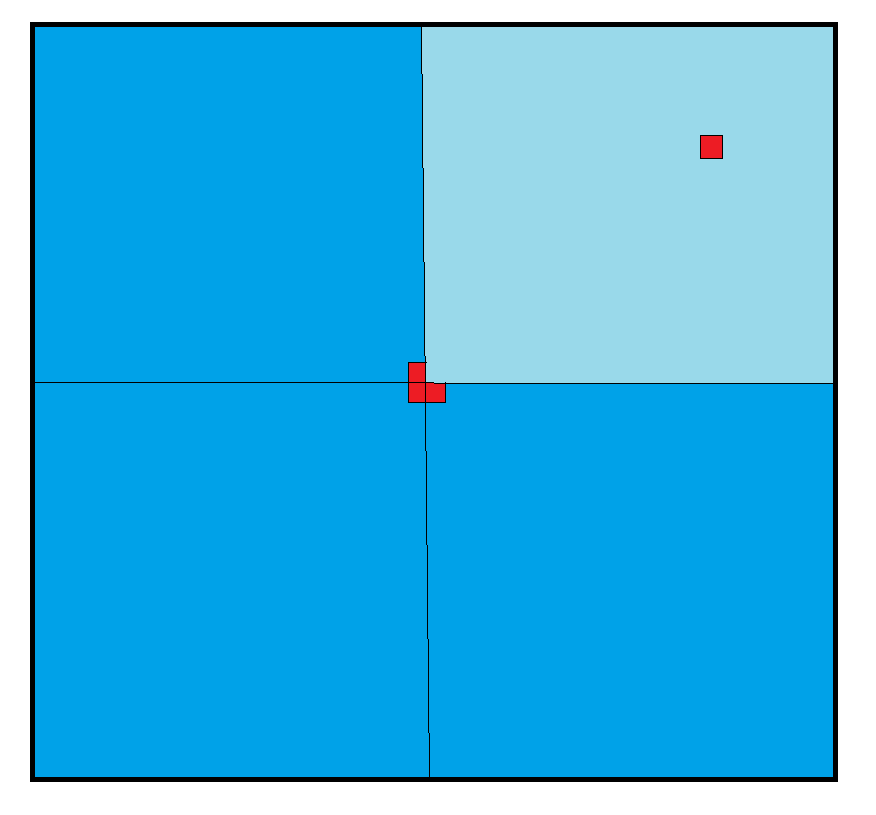
Bonjour, j'ai un exercice pour m'entraîner à la démonstration par récurrence que je n'arrive pas à résoudre :

Considérons un carré formé de 2ⁿx2ⁿ petits carrés. On enlève l'un des petits carrés.
Démontre que la surface obtenue peut être pavée par (impossible à faire, sur l'ordinateur, j'en appelle à votre imagination ) un bloc construit comme tel : 3 petits carrés : un petit carré avec un autre situé en bas de celui-ci, et un autre situé à la droite du premier. Ces blocs peuvent être tournés.

Pour le pas d'induction j'utilise donc n=1 : 2¹x2¹=4 et si on enlève un petit carré, il reste bien 4-1=3, trois petits carrés pouvant former le bloc.

Maintenant, en supposant que pour n, la surface est pavable, je dois démontrer que la surface est également pavable pour n+1 : 2ⁿ⁺¹x2ⁿ⁺¹=4x2ⁿx2ⁿ

Si j'enlève 1 : 4x2ⁿx2ⁿ-1 mais comment savoir si cette surface peut être pavée par les blocs de 3 petits carrés.
De plus, comment rédiger tout cela dans un langage bien mathématique ?

Merci de votre aide!
-----

[Tryss]

C'est assez simple :

On va considérer que l'on enlève le petit carré dans le bloc de taille 2^n * 2^n en haut à droite.

Ce bloc est pavable (par hypothèse de récurrence).

Reste à paver les 3 autres blocs :

On retire un carré du centre qui appartient à chaque autre bloc, sans ces carrés les 3 blocs sont pavables (hypothèse de réccurence) et, miracle, les 3 carrés que l'on a retirés forment le bloc de pavage.

edit : dessin pour mieux comprendre :

[invitee27a8b07]

Comme un idiot, je voulais regrouper les 4 carrés retirés au centre, et forcément, ça ne marchait pas. Effectivement, en laisser un tout seul permet de conclure en deux-deux...

[invite630d42bb]

Super merci beaucoup!!

[A voir en vidéo sur Futura]