polygone à l'interieur du cerle unité
Discussions similaires
-
Par invite2ec0a62b dans le forum Mathématiques du supérieur
Réponses: 14
Dernier message: 16/03/2012, 08h43
-
Par invite2f664770 dans le forum Mathématiques du supérieur
Réponses: 6
Dernier message: 03/01/2010, 21h20
-
Par invite16925a82 dans le forum Mathématiques du collège et du lycée
Réponses: 4
Dernier message: 27/01/2009, 22h03
-
Par invited5efedfa dans le forum Mathématiques du collège et du lycée
Réponses: 4
Dernier message: 13/09/2007, 23h51
-
Par invite5dc19622 dans le forum TPE / TIPE et autres travaux
Réponses: 0
Dernier message: 20/04/2007, 22h19




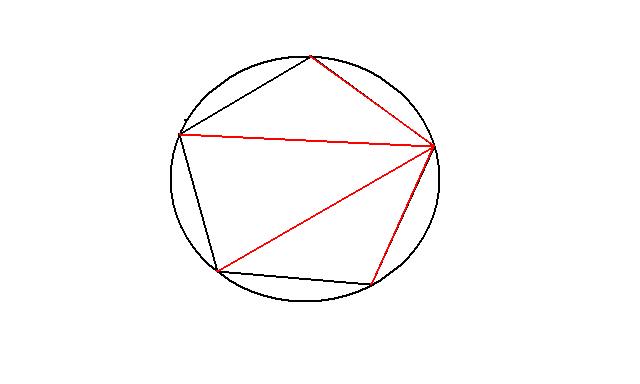

 ), on peut supposer que le point que l'on choisit est 1. Dans ce cas, la somme des distances correspond simplement à
), on peut supposer que le point que l'on choisit est 1. Dans ce cas, la somme des distances correspond simplement à