Implication

[kaderben]

Bonjour
Ci joint le fichier "implication" de l'enoncé d'un exo

V(x+Vy)=V((x+z)/2) + V((x-z)/2)
En élevant au carré:
x+Vy=(x+z)/2 + (x-z)/2 + 2/2V[(x+y)(x-y)]
soit Vy=V(x^2-z^2)
et finalement y=x^2-y^2
Même traitement pour V(x-Vy)=V((x+z)/2) - V((x-z)/2)
et y=x^2-y^2
Est ce que cette démonstration est correcte ?

Mais si on veut utiliser les principes de l'implication comme la comtraposée, le contraire comment on fait ?

Merci pour commentaires
-----

[Amanuensis]

Il me semble que non, ce n'est pas correct : vous démontrez l'implication dans le sens inverse de ce qui est demandé.

[NicoEnac]

Bonjour,

Comme l'a dit Amanuensis, c'est l'implication dans le sens inverse que vous venez de démontrer.
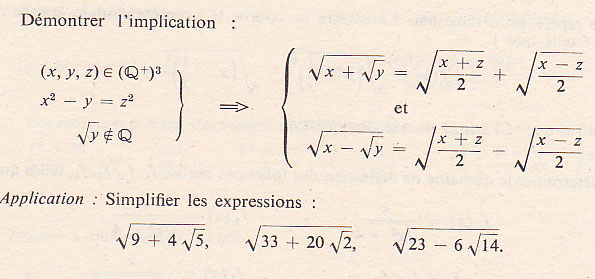
Cependant, vous pouvez utiliser un raisonnement similaire en prouvant la contraposée : supposez que . Utilisez ensuite votre raisonnement en changeant le signe "égal" par le signe "différent de" en ajoutant quelques justifications (sous quelles conditions deux nombres différents ont assurément des carrés différents ?) et le tour devrait être joué.

Edit : à mon humble niveau, je ne vois pas ce que le fait que soit irrationnel et que x, y et z soient rationnels apporte...

[Amanuensis]

Il y a un danger avec l'approche par la contraposée, danger qui correspond d'ailleurs à la partie subtile de la démonstration dans le bon sens.

Pour supposer une inégalité, il faudrait d'abord montrer qu'elle a un sens...

Il me semble que la méthode la plus simple est de prendre à l'envers les étapes de la démo dans le "mauvais sens", en prenant à chaque étape les précautions qu'il faut (ce qui va utiliser certaines des hypothèses à gauche dans l'énoncé).

Edit : à mon humble niveau, je ne vois pas ce que le fait que soit irrationnel et que x, y et z soient rationnels apporte...

Moi non plus.

[A voir en vidéo sur Futura]

[Médiat]

Bonjour,

Votre démonstration est dans le bon sens, mais elle est très imparfaite :

Il faudrait écrire votre démonstration sous la forme (la prochaine fois utilisez Latex, ce sera plus lisible) :

Attention, dans ce qui suis, je ne me suis pas préoccupé de différents problèmes (la démontration est donc toujours très imparfaite) comme les conditions sur les différentes variables que l'on peut déduire des formules, des signes des différents éléments qui sont élevés au carré (sinon pas d'équivalence)


Or (une de vos hypothèses)

[Médiat]

Pour être plus clair (et me dispenser des contraintes locales),
vous devez démontrer ()
La démarche que je vous propose, et qui est calquée sur votre premier message c'est de démontrer :

1)
2)
3)

Voire :
1)
2)
3)

Le ajouté à chaque étape vous autorise à utiliser les hypothèses de à chaque étape de la démonstration.

[kaderben]

D'après le premier message du Médiateur, ma démonstration c'est du "vite fait" car je n'ai pas utilisé les équivalences et c'est vrai, je suis un peu comme ça.
Par contre je n'ai rien compris au deuxieme message avec les B, C, D les symboles plus haut que ^
C'est un exo du niveau terminale des années 75

"à mon humble niveau, je ne vois pas ce que le fait que Vy soit irrationnel et que x, y et z soient rationnels apporte... "

Dans les exemples à simplifier, si y=16 par exemple, alors V16=4 et ça ne vaut pas le coup de donner ses expressions à simplifier.

[Médiat]

Par contre je n'ai rien compris au deuxieme message avec les B, C, D
les symboles plus haut que ^

A, B, C et D sontdes formules, et se lit tout simplement "et".