Paramétrisation de courbe et mesure de similarité entre 2 courbes

[invite3aa1ed6f]

Bonjour,

Est-il possible de paramétriser facilement une courbe (3D) composée d'autres courbes simples, du type un segment de droite relié à un arc de cercle, lui-même relié à un autre segment de droite ?

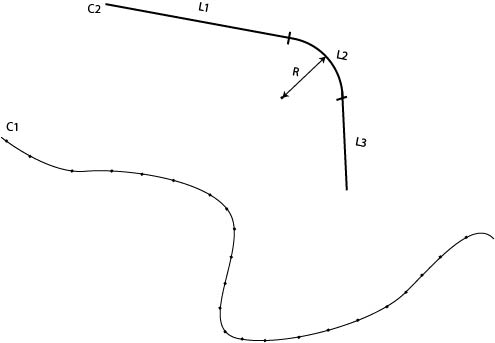
Pour situer un peu le contexte, je joins une image décrivant mon problème. La courbe est quelconque et est décrite par une succession de noeuds . La courbe est composée d'un segment de droite de longueur L1, d'un arc de cercle de longueur L2 et de rayon R, et d'un segment de droite de longueur L3. Seul le rayon R de l'arc est variable. L'objectif est de trouver le rayon R, ainsi que la rotation et la translation à appliquer à la courbe pour pouvoir fitter au mieux la courbe . La fonction à minimiser serait donc quelque chose du genre : avec la plus courte distance entre le noeud et la courbe , qui est la courbe ayant subi une rotation et une translation.

La courbe ayant des formes simples (droite et arc), j'aimerais avoir une expression algébrique pour . En supposant que peut être paramétrisée sous la forme , où t est un paramètre quelconque, on aurait , et il serait donc possible d'avoir une expression algébrique de cette distance en dérivant. Néanmoins, je ne sais pas par où commencer pour paramétriser (en 3D). Les équations paramétriques de droites et de cercles en 3D sont relativement faciles à obtenir, mais comment les combiner pour décrire ?



PS : Il se peut que mon formalisme mathématique soit un peu approximatif et mon explication un peu confuse... mes excuses pour les plus pointilleux d'entre vous =p
-----

[Dlzlogic]

Bonjour,
Ce problème ressemble à quelque-chose que je connais bien, à une nuance très importante près : vous êtres en 3D ou en 2.5D ?
En d'autres termes les points de la courbe C1 sont définis en X et Y, avec un Z : c'est du 2.5D ou en XYZ, c'est du 3D.
En particulier, si C1 est une courbe de niveau, alors c'est du 2.5D.
Apparemment, vous voulez faire du lissage. Pour faire cela je n'utilise pas des arcs de cercle, mais des arcs de parabole.
Donc, il faudrait que vous me précisiez un peu plus le contexte pour voir si je peux vous aider.

[invite3aa1ed6f]

Bonjour,

Le problème est bien 3D. Les points de C1 ont des coordonnées XYZ, et la courbe C2 peut se trouver dans n'importe quel plan.

Pour préciser un peu plus le contexte : la courbe C2 représente une partie d'un dispositif mécanique ayant une géométrie et des dimensions fixes (L1, L2 et L3), mais ayant 2 degrés de libertés "internes" (modification du rayon de courbure R (qui suit obligatoirement un arc de cercle) et orientation du plan dans lequel C2 se trouve). La courbe C2 doit se déplacer en suivant la trajectoire décrite par C1 en adaptant le rayon R et l'orientation qui permettent de coller au mieux à C1. Mon objectif est de déterminer pour chaque position sur C1 (càd au niveau de chaque noeud ) le rayon R de la courbe C2 qui permet de suivre au mieux la courbe C1.
Le problème pourrait donc s'exprimer sous la forme d'un lissage de la courbe C1, dans le sens où on cherche à fitter au mieux une version lissée (courbe C2) à C1. Mais le lissage n'est pas en soi le but recherché.

[Dlzlogic]

Bon, J'essaye de reformuler à ma manière.
Vous avez une courbe C2 constituée exactement de 3 arcs (terme général), L1, L2 et L3. L2 est un arc de cercle de rayon R pouvant varier, tangent aux segments L1 et L3.
La ligne C1 est connue.
La courbe C2 doit glisser sur C1. C2 appartient à un plan (L1 et L3 sont concourants) pouvant varier, l'autre variable étant le rayon de l'arc de cercle.
Si c'est ça, L'angle en S, intersection de L1 et L3, dans le plan de C2, est connu et fixe.
Si vous ne cherchez qu'a rendre proche l'arc L2 et la courbe C1 sur un tronçon, j'entrevois une solution, mais, sauf les points de tangence avec L2, les arcs L1 et L2 seront très différents de C1.
Si c'est ça, je crois que j'ai compris.
En résumé :
C1 est fixe et connu.
C2 est défini par l'angle en S fixe, on cherche son plan de finition et le rayon de l'arc L2.
Très intéressant.

[A voir en vidéo sur Futura]

[invite3aa1ed6f]

C'est presque cela, à deux exceptions près :
- l'angle S ne me semble pas fixe : puisque les arcs L2 et L3 sont tangents, lorsque R varie, l'orientation de L3 par rapport à L1 va également changer pour conserver la longueur de l'arc L2.
- l'objectif est de rendre toute la courbe C2 (arcs L1, L2 et L3) le plus proche possible d'un tronçon de la courbe C1. Bien sûr, étant donné la forme quelconque que peut prendre C1, une parfaite correspondance ne sera pas possible dans certains (nombreux) cas.

[Dlzlogic]

Donc la longueur de l'arc L2 est fixe et constante, ça j'avais pas compris.
Bon, ça y est je crois que c'est clair.
Le principe de la méthode est celui-là :
D'une part, on a un bout de ligne, partie de C1. Sa longueur est approximativement L1+L2+L3.
Ce bout de ligne est constitué de N points (au moins 4), mais si j'ai compris, il y en aura plus.
D'autre part on a une ligne C2 constituée de
1 segment L1, je ne sais pas ce qui est fixe, sa longueur ?
1 arc de cercle L2 de longueur fixe
1 segment L3, je ne sais pas ce qui est fixe.

On calcule 5 points : les extrémités des segments et le milieu de l'arc de cercle en fonction d'un certain nombre de variables, en particulier R et 3 valeurs soigneusement choisies. Ces 3 valeurs caractérisent le plan contenant la ligne C2
On calcule la distance de ces 5 points à la ligne C1, tout ça bien-sûr en fonction des variables.

La formule de transformation de C2 vers C1 s'écrit
X = TX + XX.x + XY.y + XZ.z
Y = TY + YX.x + YY.y + YZ.z
Z = TZ + ZX.x + ZY.y + ZZ.z
X,y,z sont les coordonnées de départ, X,Y,Z les coordonnées d'arrivée
Et le reste, ce sont 12 paramètres à calculer. D'où le nombre minimum de 4 points.
Mais si les calculs sont bien menés la valeur de ces 12 paramètres sera sans intérêt.

Ensuite, on écrit que la somme des carrés des distances des 5 points à C1 doit être minimum.
Cette valeur sera minimum pour les valeurs qui annulent sa dérivée.
On écrit les dérivées partielles, normalement 4 (R et Vx,Vy,Vz), et on écrit qu'elles sont nulles.
On obtient ainsi 4 équations linéaires. on a 4 variables, donc normalement ce système admet une solution.
Les termes paramètres des ces équation devraient être de la forme S(x) S(Xy) S(X²) etc.
Si on n'arrive pas à éliminer les paramètre de changement de repère, il y aura plus d'équations, mais c'est pas grave.

A mon avis il faut faire très attention au choix des 3 paramètres définissant le plan. Mais je pense que c'est votre dispositif mécanique qui déterminera ce choix.

En gros, les 2 étapes qui me paraissent les plus difficiles, c'est calculer les coordonnées des 5 points et calculer les distances à C1. Cette seconde partie est certainement la plus délicate.

Tenez-moi au courant.

[invite3aa1ed6f]

Merci pour votre aide. Je vais cogiter là-dessus et vous tiendrai au courant.

Pour répondre à vos dernières interrogations concernant les dimensions de C2 : les longueurs des 3 arcs L1, L2, L3 sont fixes.

[Dlzlogic]

Donc, effectivement la seule variable dans le plan de C2 est bien R.
Le problème de calcul des distances des 5 points à C1 est difficile. Il est bien possible qu'il faille faire des itérations, type Newton. Même dans le cas où il n'y a aucune variables, c'est un problème difficile.

[Dlzlogic]

Il me vient une idée : serait-t-il possible par un changement de repère astucieux de transformer C1 en fonction strictement monotone ? Au moins sur le tronçon concerné ?
En ce cas, le problème de calcul de distance serait largement simplifié.

[invite3aa1ed6f]

Je ne pense pas que cela soit possible. La courbe C1 est vraiment quelconque et peut, à priori, prendre n'importe quelle forme.

Concernant le calcul des distances, je pensais prendre le problème dans l'autre sens :

• paramétriser la courbe C2 en fonction de R, de la normale au plan contenant C2, et d'un paramètre qui servirait à parcourir la courbe C2. On aurait donc qqch comme .
  
• en considérant seulement un tronçon de C1, calculer la plus courte distance entre chaque point de ce tronçon de C1 et la courbe C2. Cela pourrait se faire en annulant la dérivée par rapport à s de .
  
• calculer la somme des carrés des distances obtenues au point précédent et minimiser cette somme.
  

En 2D, la paramétrisation semble faisable si l'on considère l'origine du repère au début de L1, l'axe x aligné avec L1 et l'axe y pointant 'vers le haut'. On obtient alors des équations paramétriques "par morceau" :

pour t dans [0,L1] :




pour t dans [L1,L1+L2] :





pour t dans [L1+L2, L1+L2+L3] :






Néanmoins, je ne suis pas encore arrivé à généraliser cela en 3D. Cette approche vous semble-t-elle valable ?

[invite3aa1ed6f]

Dans les équation paramétriques, t équivaut au paramètre de parcours s.
(Je n'arrive pas à éditer mon message précédent)

[Dlzlogic]

Bonjour, l'idée ne parait pas mauvaise, en effet calculer les distances des point de C2 par rapport à C1 donne le même résultat que calculer les distances des points de C1 par rapport à C2, mais effectivement L2 étant un arc de cercle, c'est plus simple.
Je que je n'imagine pas vraiment, c'est comment la façon de trouver le tronçon de C1 concerné. Et aussi, combien de points de C1 appartiendront à la longueur (L1+L2+L3).
Tout ça n'est pas évident du tout.
... au bout de 5mn on ne peut plus modifier un message.
Sinon, j'avais compris.

[invite3aa1ed6f]

Bonjour,

Je suis finalement parvenu à paramétriser la courbe en 3D (voir l'image jointe, ainsi que le fichier pdf). On suppose les points a1 et a2 connus. a3 peut se déduire à partir de l'équation décrivant la portion L2 avec s=L1+L2.
Par contre, je bloque sur la résolution de l'équation annulant la dérivée par rapport à s pour le tronçon L2 (dernière équation du pdf)...

Concernant vos interrogations, voici ce que je pensais faire. La courbe C2 glisse sur la courbe C1 et, pour chaque "position" durant ce glissement, on essaie de trouver le rayon de l'arc L2, la translation et la rotation de C2 permettant de fitter C2 à C1. Pour chaque "position" durant le glissement, on restreint le déplacement du point a1 au plan normal à C1 et passant par le point "courant" de C1 (voir ligne verte sur l'image). De cette manière, on peut définir un tronçon de C1 sur lequel il faut fitter C2 : le tronçon commence au point "courant" (ligne verte) et se termine environ L1+L2+L3 plus loin. La difficulté est de définir ce "environ" L1+L2+L3 plus loin.

centerlineFitting.jpgeq.pdf

[Dlzlogic]

Bonjour,
J'ai lu votre calcul, mais j'avoue que la symbolique me déroute un peu.
Par ailleurs, ce qu'il faut minimiser est la somme des carrés des distances, sans distinction de L1, L2 et L3, et non pas, séparément les distances par rapport aux 3 arcs.
D'autre part, les inconnues dont on cherche à déterminer la valeur n'apparaissent pas vraiment dans le calcul.

Voila ma version de ce problème :

Adaptation d'une courbe C2 à une courbe C1

Hypothèses
La courbe C1 est une ligne brisée constitués de n points P1 à Pn
La courbe C2 est constituée exactement d'un segment de droite de longueur L1, d'un arc de cercle de longueur L2 et d'un segment de droite de longueur L3. L'arc de cercle est de rayon R et est tangent aux deux segments. La longueur de la courbe C2 est donc L1 + L2 + L3.
On appellera E1, E2, E3 et E4 les extrémités des segments et O le centre de l'arc de cercle.
On cherche à définir le rayon R et la transformation (rotation + translation) qui fera correspondre "au mieux" la courbe C2 au tronçon étudié de C1.

Par convention les coordonnées dans le système général, c'est à dire celui de la courbe C1 seront en majuscule (X,Y,Z)


Méthode proposée.

La transformation pour passer du repère de C2 au repère général est
X = TX + XX.x + XY.y
Y = TY + YX.x + YY.y
Z = TZ + ZX.x + ZY.y
De plus les 9 paramètres sont liés par la relation X² + Y² + Z² = x² + y².
En effet, le repère de C2 est le plan horizontal et il n'y a ni homothétie ni affinité.

Choix d'un repère pour C2.
Je choisis le repère tel que L1 ait pour coordonnées e1=(0;0) e2=(L1;0)
J'adopte la convention que si O est à droite de L1, alors R est positif.
J'appelle T l'angle au centre de L2, alors L2=R.T et T a naturellement le signe de R (ma convention pour les angles est le sens horaire).
Coordonnées de o (L1 ; -R)
Coordonnées de e3 =(L1 + R.sinT ; -R + R.cosT);
Coordonnées de e4 = (L1 + R.sinT + L3.cosT ; -R + R.cosT -L3.sinT);

Rappelons que T est défini par L2=R.T

Recherche du tronçon de C1 concerné.
Prenons l'hypothèse que on connait le point de départ Pi de C1 où sera le point E1.
On peut donc écrire
XA1 = TX + XX.xe1 + XY.ye1
YA1 = TY + YX.xe1 + YY.ye1
ZA1 = TZ + ZX.xe1 + ZY.ye1
Comme xe1 = ye1 = 0, alors TX, TY et TZ sont déterminés.

Evaluons la distance d'un point de C1 par rapport à C2
1- cette distance ne sera à condidérer que si la projection de Pi appartient à l'arc de C2 étudié.
2- pour un segment, c'est la longueur de la projection orthogonale sur le segment (L1 ou L3)
3- pour l'arc L2, c'est la différence à R de la distance à O, centre de l'arc.
4- on ne sait pas, a priori, le signe du rayon. il semble intéressant de l'étudier dès le début.

On aura pris soin de calculer les distances curvilignes des points P de la courbe C1. Cependant, étant donné que la longueur d'un segment est toujours plus courte que celle de l'arc ayant les mêmes extrémités, cette distance curviligne devra être ajustée en permanence.

Pour chaque point Pi (sauf le premier qu'on a considéré comme point de départ), on peut écrire le carré de la distance avec comme paramètres XX, XY, YX, YY, R.
L'angle pose un problème, puisque sa définition dépend de R. On ne sait pas écrire une relation algébrique directe. Une méthode pourrait consister à avoir 2 paramètres supplémentaires cosT et sinT.

Les formules donnant les carrés des distances aux arcs sont un peu longues et compliquées et sont des fonctions de XX, XY, YX, YY et R (éventuellement cosT et sinT) et des paramètres Pi(X,Y).
On écrit que la somme de ces distances au carré doit être minimum, cela se traduit par écrire que les 5 dérivées partielles s'annulent. Reste le problème de T qu'il faudra contourner, éventuellement par un développement limité au 2è ordre.

Il doit en résulter un système, de préférence linéaire, qui doit admettre une solution unique.
Il est possible que si le calcul a imposé de faire une approximation, en particulier la position du point de départ, cette solution servira de solution approchée de départ pour un nouveau calcul. Mais cette dernière option devrait être étudiée ultérieurement.

Il serait intéressant pour avoir une idée plus précise du problème, de connaitre l'aspect de la ligne C1, c'est à dire l'ordre d'idée de la longueur des segments qui la composent, en comparaison avec les longueurs L1, L2, L3.
Par ailleurs, je pense que la méthode qui consisterait à avoir une approximation plans du tronçon de C1 étudié n'est pas à rejeter.

[invite3aa1ed6f]

Bonjour,

Désolé pour mon formalisme mathématique assez approximatif.
Les équations que j'ai écrites ne sont qu'une étape de votre méthode. Elles ne servent qu'à calculer la distance entre la courbe C2 (qui n'a pas encore subi de rotation/translation, mais il suffit de faire une changement de variable pour rajouter la rotation et la translation) et un point de la courbe C1. Concernant ce calcul de distance, comment déterminer s'il faut calculer la distance par rapport à L1, L2 ou L3 ? Mon idée était donc d'utiliser un paramètre s qui permet de parcourir C2, et d'exprimer la distance entre un point et C2 en fonction de ce paramètre. Il faut alors de chercher la valeur du paramètre s qui permet d'avoir la plus courte distance entre le point et C2. Cette méthode permettrait de sélectionner la partie de C2 (L1, L2 ou L3) par rapport à laquelle calculer la distance entre un point et C2. Je ne sais pas si vous pensiez à une autre méthode pour ce calcul de distance ?

L'image attachée montre la forme approximative de C1. La distance entre chaque point de C1 est de l'ordre de 0.5mm. La longueur totale de C1 est d'environ 1000mm. Les longueurs de L1, L2, L3 sont respectivement d'environ 40mm, 30mm, 60mm.

[Dlzlogic]

Bonjour,
Une réponse rapide en attente de validation de l'image.
J'ai encore pensé à votre problème. Il se trouve que une équation contenant un angle et sa ligne trigonométrique ne peut pas être résolue algébriquement. La méthode le plus couramment utilisée est celle de Newton. Par contre, il existe des méthodes de résolution de systèmes non linéaires.

La pièce représentée par C2 mesure donc 130 mm et sur cette distance il y a environ 260 points de C1.

Il faut savoir que l'arc de cercle est difficile à manipuler dans les calculs. On préfère généralement l'approximer par une suite d'arcs de parabole.

Concernant le calcul de distance à une ligne, c'est un problème difficile lorsqu'on connait numériquement les lignes et points, ici tout est paramétré. D'où la seule valeur numérique à peu près connue et indépendante, c'est l'abscisse curviligne. Etant donné le très grand nombre des points de C1, par rapport à C2, cette valeur peut être considérée comme bonne, et il ne faudra même pas faire d'ajustement. Grâce à ce très grand nombre, le point de départ peut être définitif, pour 1 calcul, en abscisse curviligne.

Vous allez me trouver très terre à terre, j'essaye toujours de me représenter le phénomène réel. Donc, j'imagine que le ligne C1 est un tuyau d'un certain diamètre, et la courbe C2 une petite pièce qui admet de se courber plus ou moins, et que l'on doit faire glisser à l'intérieur du tuyau (Je brule ?).
Question : quel est l'angle maximum entre le segments L1 et L3 ?

Je laisse, dans un coin de me tête, l'idée d'un calcul préliminaire d'ajustement de la courbe C1, par tronçon.

[invite3aa1ed6f]

Vous avez bien deviné : il s'agit d'une petite pièce se baladant dans un tuyau ayant une forme assez particulière.

Le rayon de L2 va de 30mm à l'infini. Donc, l'angle maximal serait d'environ 60°.

[Dlzlogic]

Bon, à mon avis, puisqu'il semble qu'il s'agit d'une étude ponctuelle avec éventuellement de petites variantes, suivant certains cas, il vaudrait mieux faire un calcul exactement adapté au problème et non pas un calcul général avec application au cas précis.
La méthode serait la suivante : connaissant la ligne C1, on commence par isoler les tronçons les plus critiques, c'est à dire ceux qui présentent une courbure la plus forte. Je suppose qu'on a une notion assez précise de l'écart maximum de cette courbure maximum.
Il me manque une information, dites-moi seulement si la valeur l'angle est fixée par un moyen quelconque par une commande extérieure, ou à l'inverse, la valeur numérique de cet angle, on s'en fiche, il s'adaptera tout seul.
J'avoue aussi que j'ai un peu de mal à comprendre comment on arrive à forcer l'élément L2 à être un arc de cercle.
J'imagine bien qu'il y a un côté confidentiel, on peut aussi communiquer par MP, et vous pouvez me contacter sur mon site http://www.dlzlogic.com.
Mais encore une fois, il me parait plus simple de partir de la ligne C1 à parcourir, que d'essayer d'adapter la ligne C2.
Le fait qu'on ait une équation qui contienne un angle et sa ligne trigonométrique complique largement le problème sur le plan mathématique.