Bonsoir,
J'ai fait un exercice, cependant je n'ai pas de correction, j'aimerais savoir ce que vous en pensez (je suis pas du tout mais pas du tout persuadé de ma preuve, surtout que mon majorant dépend d'une de mes variables).
Enfin, je voudrais plutôt qu'on m'aide à le résoudre car je pense qu'il est faux
Cordialement,
-----





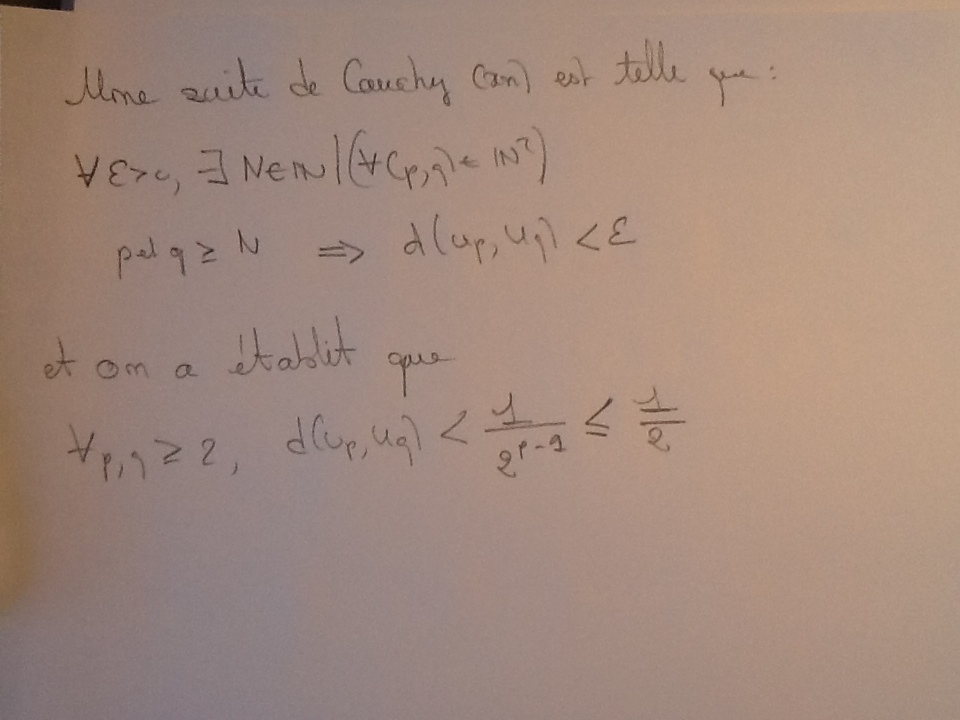
 , or vous avez fait une démonstration pour
, or vous avez fait une démonstration pour