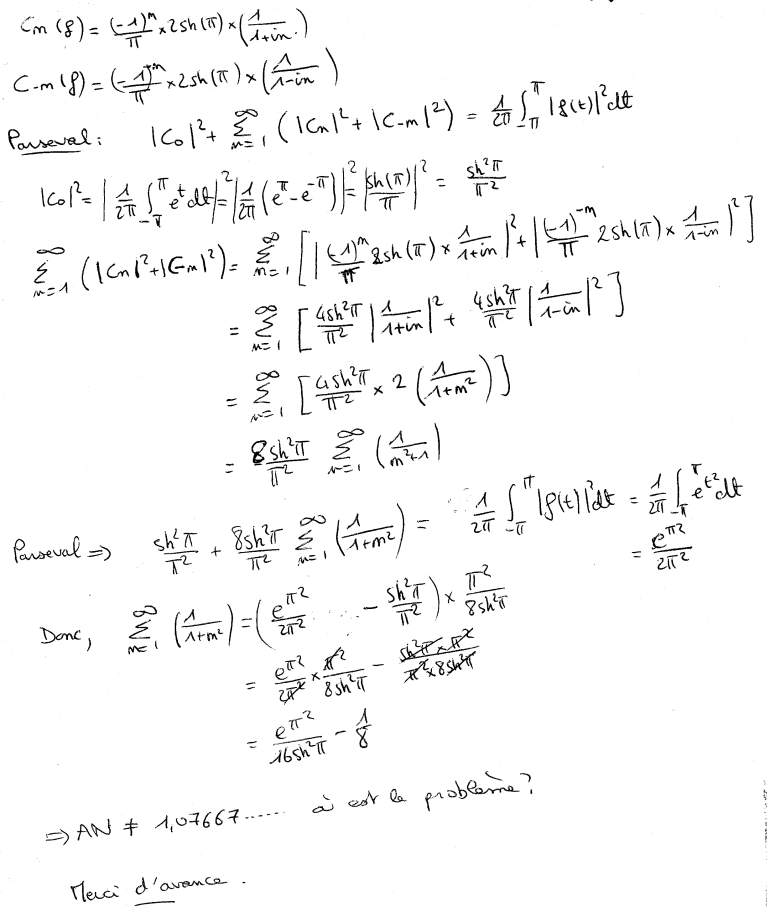série de Fourier

[invite4c80defd]

Bonsoir à tous,
je suis en train de faire un exo avec lequel je rencontre des problèmes.
on considère la fonction définie par f(t)=exp(t) 2pi-périodique, pour tout t appartenant à [-pi,pi[ .

on me demande de calculer les calculer les coeff de fourier exponentiels de f (je ne l'ai jamais fait).
il faut ensuite en déduire la valeur de la somme sigma de 1 à +infini de (1/(n²+1)) et sigma de 1 à +infini de (-1)ⁿ*(1/(n²+1)

j'ai utlisé la premiere formule du lien: http://www.bibmath.net/dico/index.ph...rierserie.html pour trouver C_n(f) et C_-n(f).

(j'ai pris l'intégrale de -pi à pi)

j'en suis à:
C_n(f)=1/2pi(1-in)(exp(pi(1-in))-exp(-pi(1-in)))

C_-n(f)=1/2pi(1+in)(exp(pi(1+in))-exp(-pi(1+in)))

et C₀(f)=1/(2pi^2)(exp(pi)+exp(-pi))

seulement, quand j'applique le theoreme de dirichlet
C₀ + sigma de 1 à +infini de(C_n*exp(int)+C_-n*exp(-int)), j'obtient des formules énormes et je m'embourbe dans des calculs incroyables...
j'ai du oublié quelque chose ou peut etre peut-on simplifier un peu mais je ne vois pas trop où ...quelqu'un aurait-il une idée ?


merci d'avance
-----

[gg0]

Bonsoir.

Pourquoi le théorème de Dirichlet ? Celui de Parseval, très simple avec la série complexe suffit certainement.

Cordialement.

[invite4c80defd]

ok , je vais essayer avec la première formule du lien : http://www.bibmath.net/dico/index.ph.../parseval.html

par contre, que dites vous des coefficients Cn(f) ? pourraient-ils , si ceux-ci sont corrects être rendus plus faciles à manipuler ?

merci

[invite4c80defd]

j'ai essayé mais en vain.
je me demande une chose: l'égalité de Parseval fait apparaitre des carrés partout, et du coup, de me retrouve avec quotients qui ont au dénominateur (1+n^2)^2 , or, moi je voudrait seulement du 1+n^2....comment dois-je procéder ?

[A voir en vidéo sur Futura]

[gg0]

Je ne comprends pas ...
Les carrés des modules des c_n donnent des 1+n² au dénominateur.
Sinon, je n'ai pas vu de différence entre tes coefficients et ceux affichés par mon esclave formel. A condition de lire ton 1/2pi(1-in)(exp(pi(1-in))-exp(-pi(1-in))) comme étant 1/[2pi(1-in)](exp(pi(1-in))-exp(-pi(1-in)))

Cordialement.

[invite4c80defd]

oui on a bien (exp(pi(1-in))-exp(-pi(1-in)))*1/[2pi(1-in)], désolé pour l'écriture...
j'ai un probleme quand je prend le module de l'expression ci-dessus.

en fait, je prend le module de 1/[2pi(1-in)] que multiplie le module de (exp(pi(1-in))-exp(-pi(1-in)))

on a donc module(1/[2pi(1-in)]) * module(exp(pi(1-in))-exp(-pi(1-in)))

ce qui donne (sauf erreur): 1/2pi*module(1/(1-in))*module(exp(pi)*exp(-inpi)-exp(-pi)*exp(inpi))

or module(exp(-inpi))=module(exp(inpi))=1 et module(1/(1-in))=(n+1)/[(1+n^2)^2] si je ne me trompe pas.

et donc, il y aurait des carrés..mais je ne comprend d'où viennent mes erreurs..

[gg0]

Bonjour.

si je ne me trompe pas

Désolé, mais tu te trompes.
Un calcul de niveau terminale donne :


Je ne sais pas où tu es allé chercher ce carré de la somme des carrés de la partie réelle et de la partie imaginaire.

Rappel : Plus l'expression est longue et compliquée, plus il faut être strict dans l'application des règles.

Cordialement.

[invite4c80defd]

ah oui , je me suis trompé en voulant multiplier par le conjugué.
donc, on aurait:
vu que module(exp(-inpi))=module(exp(inpi))=1 et module(1/(1-in))=1/(1+n^2),

1/2pi*module(1/(1-in))*module(exp(pi)*exp(-inpi)-exp(-pi)*exp(inpi))=1/2pi*sigma(1/(1+n^2))*(exp(pi)-exp(-pi))^2

et la seconde partie de l'égalité de parseval donne: l'intégrale de la fonction au carré entre -pi et pi: exp(pi^2)/(2pi^2)

donc, exp(pi^2)/(2pi^2)=1/2pi*sigma(1/(1+n^2))*(exp(pi)-exp(-pi))^2

en donc,sigma(1/(1+n^2)) pour n allant de 1 à +infini vaudrait exp(pi^2)/(2sh(x))^2

avec sh(x)=(exp(x)-exp(-x))/2

mais quand on regarde la valeur de cette expression, il y a un probleme quelque part ...

[invite4c80defd]

c'est sh(pi) et pas sh(x) dsl.

[invite4c80defd]

je crois que j'ai trouvé une source d'erreurs.
en fait, dans le lien que j'ai donné, on calcue l'intégrale de -infini à + infini , et j'ai fais comme si je la calculait de 1à + infini.
j'ai recommencé les calculs de cette facon:
exp(pi^2)/2pi^2=|Co|^2+sigma de 1 à +infini de (|Cn|^2+|C-n|^2)
et j'ai trouvé , mais je ne sais pas du tout si c'est correct:
exp(pi^2)/16(sh(pi))^2 - pi/4sh(pi)
qu'en dites-vous ?

[gg0]

Je ne comprends pas ce que tu racontes : "on calcule l'intégrale de -infini à + infini " ?? Tu veux dire la somme, non ?
Effectivement, si on veut avoir une série habituelle, il va falloir regrouper c_n et c_-n. Mais n'importe comment, je ne vois pas comment tu as trouvé le module de exp(pi)*exp(-inpi)-exp(-pi)*exp(inpi). on dirait que tu as pris la différence des modules !! erreur grave, la fonction valeur absolue, et sa généralisation aux complexes, le module, ne sont pas linéaire : |5-(-7)| ne peut pas être égal à |5|-|-7| qui est négatif !

Donc un calcul à revoir ...

Cordialement.

NB : Tu fais quand même beaucoup d'erreurs de calcul sur des notions de lycée !!

[invite4c80defd]

oui c'est la somme excusez-moi.
pour le module, je me suis servi du fait que |exp(-inpi)| =|exp(inpi|=1, ce qui je pense est correct.
mais il est vrai que je ne suis pas sur du carré du module de exp(pi)*exp(-inpi)-exp(-pi)*exp(inpi), qui donne quel résultat sinon (exp(pi)-exp(-pi))^2 ?

merci d'avance

[gg0]

"oui c'est la somme excusez-moi." pas plus !!!
Tu continues à inventer, au lieu d'appliquer des règles du lycée.
Rappel : et en général, il n'y a pas égalité. Donc ça ne sert à rien pour calculer le module d'une somme ou d'une différence !

Prenons par exemple n=3 :
exp(pi)*exp(-inpi)-exp(-pi)*exp(inpi)=-exp(Pi)+exp(-Pi) dont le module est exp(Pi)-exp(-Pi)
Je n'utilise pas le module de exp(-inpi) ou exp(inpi), ce sont des réels bien connus.

Allez, à toi de faire bien ... et de justifier que ton résultat est le bon.

Cordialement.

[invite4c80defd]

ok merci pour ce rappel, j'oublie toujours l'inégalité.
pendant ce temps, je réfléchissais à une chose:

exp(pi)*exp(-inpi)-exp(-pi)*exp(inpi)=exp(pi)*(-1)^n-exp(-pi)*(-1)^n
mais du coup, lorsque je désire en prendre le module, en factorisant par (-1)^n, ne trouverait-on pas exp(pi)-exp(-pi) ?

[invite4c80defd]

ne trouverait-on pas exp(pi)-exp(-pi) plus facilement je voulais dire

[gg0]

Si, bien sûr.

par curiosité, je suis allé voir la suite, ça marche bien. On trouve la valeur exacte de la série, dont une valeur approchée est 1,076674047.

Bonne soirée !

[invite4c80defd]

voila ce que j'ai essayé de faire, où serait-mon (ou mes) probleme(s) selon vous ?

[invite4c80defd]

l'image est-elle lisible ? si ce n'est pas le cas, je peux le rescanner avec une meilleure qualité ...n'hésitez-pas !

[gg0]

oui, l'image est lisible (maintenant qu'elle a été validée).

Je n'ai pas la même valeur pour c_n (pas de 2) et surtout pas le même résultat pour l'intégrale de f(x)².

Attention, le carré de n'est pas mais d'après les formules sur les puissances vues dès le collège. Toujours le même problème, de faire vraiment les calculs.
Force toi à calculer juste, c'est à dire à systématiquement appliquer des règles de calcul, à ne rien écrire qui ne soit l'application stricte d'une règle.

Cordialement.

[invite4c80defd]

j'ai corrigé mes erreurs de calculs, je retombe bien sur la valeur dont vous parliez.

j'ai encore un probleme car la derniere partie de l'exo consiste à calculer la somme de la série sigma de 1 à + infini de (-1)^n*(1/(1+n^2))

j'ai regardé le comportment de cette nouvelle série et un terme sur deux est négatif. je pense que cette série paut etre décomposée en deux séries:
sigma de p allant de 0 à +infini de (1/(1+(2p)^2)) - sigma de p allant de 0 à +infini de (1/(1+(2p+1)^2)) , c'est-a-dire que l'on ajoute tous les termes pairs en soustrayant les impairs , mais comment calculer ces deux séries ?
(je précise que c'est la premiere fois que je fais ce genre de chose)

merci d'avance

[gg0]

En soustrayant 2 fois la série des termes d'ordre pair (ceux qui sont positifs), tu retombes, au signe près sur ta série. Et la série des termes d'ordre pair a beaucoup de lien avec celle que tu as traitée.

Cordialement.

[invite4c80defd]

ok donc on a:
somme de série recherchée=somme de sérié calculée avant - 2*sigma de 1 à +infini de (1/(1+(2p)^2))
reste à trouver sigma de 1 à +infini de (1/(1+(2p)^2)) connaissant sigma de 1 à +inf de 1/(1+n^2).

j'ai essayé de modifier l'expression de 1/(1+(2p)^2) mais sans grand succès
j'ai ensuite essayé un changement de vairable mais là , je ne suis pas sur de moi:
posons q=2p
alors sigma de 1 à +infini de (1/(1+(2p)^2)) =sigma de 2 à +infini de (1/(1+(q)^2)) = sigma de 1 à +infini de (1/(1+(q)^2)) -1/2.
alors le série des pairs vaudrait le résultat que l'on a trouvé pour la première série -0.5 ? (je demande confirmation, cela parait trop simple).

et du coup, somme série recherchée= -(somme sérié calculée avant -2*le résultat ci-dessus ) .

merci d'avance

[gg0]

Je crains de t'avoir envoyé sur une fausse piste .. Désolé.

Non la série des pairs ne donne aps le résultat de la série complète (vu que les termes sont tous positifs, si on en enlève, ça fait moins !). q ne prend pas toutes les valeurs de 1 à l'infini, il ne prend même pas la valeur 1.

Pour l'instant, je n'ai pas trop d'idée.

[invite4c80defd]

ce n'est pas grave, dites-moi dès que vous aurez une nouvelle piste à me proposer.
merci

[gg0]

Finalement,

c'est simple, la série avec les (-1)ⁿ s'obtient en calculant de deux façons f(0).

Cordialement.

[invite4c80defd]

je veux bien vous croire lorsque vous dites que c'est simple, mais je n'est pas saisi ce que vous désirez faire en calculant f(0)..pourriez-vous détailler un peu svp ?


merci d'avance

[gg0]

Ben .. tu as la fonction et tu as sa série de Fourier. En 0 elles sont égales. ça permet de calculer la série demandée ...

[invite4c80defd]

comme je vous l'ai dit, je viens de commencer sur ce theme, j'ai donc plusieurs questions.
comment savez-vous qu'en 0, la sériede fourier de f (notons la S(f)(t) )et f(t)=exp(t), sont égales? est-ce toujours le cas ? (j'avoue etre un peu perdu..)
deplus, si tel est le cas, comment la série de fourier de f qui vaut sigma de 1 à +inf de (Cn(f)*exp(int)) pour t=0 (avec f(0)=exp(0)=1) peut mener au résultat voulu ?
car sigma de 1 à +inf de (Cn(f)*exp(int)) pout t=0 vaut :sigma de 1 à +inf de (Cn(f)) avec Cn(f)= l'expression de ma feuille jointe (sans le 2 évidemment)

merci de votre aide

[gg0]

1) "comment savez-vous qu'en 0, la série de Fourier de f (notons la S(f)(t) )et f(t)=exp(t), sont égales?" question de cours. Ce devrait être évident pour toi, donc réapprends tes leçons.
2) "la série de Fourier de f qui vaut sigma de 1 à +inf de (Cn(f)*exp(int)) pour t=0" Non, c'est totalement faux. Relis ce qu'est la série de Fourier complexe. Le pire est que tu le savais précédemment.

"j'avoue être un peu perdu" : Oui, donc prends le temps de reprendre tes esprits, relis ton cours et aussi le début de l'exercice. Rien de compliqué ici.

Cordialement.

[invite4c80defd]

ah oui , je confond tout.....
la série de Fourier complexe de f devait etre : S(f)(t)=Co +sigma de 1 à +inf ( Cn(f)*exp(int)+C-n(f)*exp(-int) ).
analysons cela en 0.
S(f)(0)=Co+sigma de 1 à +inf ( Cn(f)+C-n(f) ) du coup .
je remplace Cn(f)+C-n(f) par leurs expressions ma feuille jointe (sans le 2).
j'ai simplifier et finalement trouvé: série avec les (-1)^n = pi/(2sh(pi)) -0.5
etes-vous d'accord sur ce résultat ?

merci