Surjection dm.

[topmath]

Bonsoir à tous :
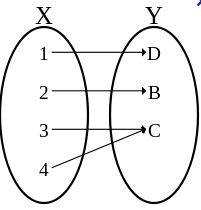
Salut planeteF tous ce que vous avez évoquer est très claire , est justement il faut que je maitrise à fond la définition classique et même les de autre définitions à savoir ainsi que Set car j'ai un grand travail qui m'attend utilisant la surjection ,injection , bijection certainement vous devez les connaitre "La décomposition canonique d'une Application" plus tard "les morphisme de groupes " je ne sais si vous acceptez d'autre question ultérieurement et merci d'avance .

Cordialement
-----

[topmath]

Bonsoir à tous : D’après ce diagramme j'ai sus une chose sur la surjection :


Que tout y appartenant à Y est en relation avec aux moins un x appartenant à X , et que chaque x de X ne peut rester sans relation avec un élément y de Y , aussi et que tout x de X ne peut etre en relation avec deux élément de Y en même temps (si je puisse dire ça ) est ce vrai ?

Cordialement

[gg0]

Je croyais que tu connaissais la définition de "surjection". Là, tu reviens au B A BA !

Si f est une fonction de X dans Y, elle est surjective si "tout y appartenant à Y est en relation avec au moins un x appartenant à X"; on dit plutôt "tout y appartenant à Y est image d'au moins un x appartenant à X", car le vocabulaire des fonctions distingue bien l'ordre de la relation :
f est une fonction de X dans Y si f est une relation de X vers Y telle que si y et y' sont différents, on n'a jamais (x f y et x f y').
Dans x f y, qu'on note classiquement y=f(x), x est un (*) antécédent de y et y l'image (*) de x. la condition dit qu'un élément de X ne paut pas avoir deux images différentes.

On appelle souvent application de X dans Y une fonction telle que tout élément de X a une image. Dans ce cas ce que tu dis ("chaque x de X ne peut rester sans relation avec un élément y de Y") est vrai. mais pas dans le cas général.
Pour certains, une surjection est effectivement une application surjective.

Donc il est important de savoir de quoi on parle.

Cordialement

(*) Un antécédent parce qu'un y peut avoir plusieurs antécédente; l'image parce que il y a une seule image quand il y en a une.

[topmath]

Bonjour à tous :

On appelle souvent application de X dans Y une fonction telle que tout élément de X a une image. Dans ce cas ce que tu dis ("chaque x de X ne peut rester sans relation avec un élément y de Y") est vrai. mais pas dans le cas général.
Pour certains, une surjection est effectivement une application surjective.
Donc il est important de savoir de quoi on parl

Alors si je comprend bien l'ensemble de départ X est contenue dans l'ensemble d'arrivée Y ? merci d'avance .

Cordialement

[gg0]

Non, non,

X n'a aucune raison d'être un sous-ensemble de Y.

On dit application de .. dans ... ou application de ... vers .... Ce sont des expressions toutes faites.

Voici une application de {1;2} dans {5;6;7} : f={(1,6},(2,6}}. On écrit plus souvent "f est définie par f(1)=6 et f(2)=6".
dans cet exemple, f n'est pas surjective (5 n'a pas d'antécédent), ni injective (6 a deux antécédents différents)
En voici une, injective, de {1;2} dans {5;6;7} : f={(1,6},(2,5}}. On écrit plus souvent "f est définie par f(1)=6 et f(2)=5".
Et il est facile de comprendre qu'il n'y a pas d'application sujective de {1;2} dans {5;6;7} (à cause de l'unicité de l'image).

Cordialement.

[topmath]

Bonjour à tous :
Premièrement merci @gg0 pour votre passionse avec mais questions très élémentaire :

Un détaille seulement lors de la démonstration pour ce qui est de la question je cite :

Bonjour à tous :Je connais la définition de la surjection mais voilà je ne sais pas si cette réponse est juste à ma propre question ?

Question : Peut on dire que est surjectif de si ?
Repense:J'applique bêtement la définition quelque soi alors telque alors f est surjective.

Merci d'avance de m'orienter .

.
Après correction de cette réponse c-a-d :

Solution proposé :

Surjectif : Nous cherchons un élément tel que .Le réel est convient ! je ne sais si c'est juste ou faut merci d'avance pour votre correction .
Cordialement

Il y'a quelque part une confusion que j'ai du mal à comprendre dans la réponse proposer ci haut (supposer oublier) , pour trouver par apport à y (utile pour la démonstration de la surjection ) j'ai pas considérer le cas ou veux dire le cas ou ou si je comprend bien ça n’influe pas sur la démonstration si on là prenne pas en considération ? et merci d'avance .

Amicalement

[inviteb3412e7c]

Pour la démonstration de la surjection d'une application on cherche qu'un antécédent pour chaque , mais il peut y en avoir d'autre. Donc tu as raison, si on trouve d'autres antécédents des que ceux qui ont été mis en évidence dans la démonstration, mais on n'a pas été obligé de les regarder.

D'ailleurs tu aurais pu faire une démonstration équivalente en regardant que les sans regarder les nombre en utilisant comme antécédent de , .

[gg0]

Topmath,

on fait des maths, pas de la littérature : Si on a trouvé un antécédent, c'est bon. Pas la peine d'épiloguer.
Pour l'instant, tes questions ressemblent plus à un essai de trouver un défaut sans vraiment t’occuper de la définition et de comment t'en servir. Car l'essentiel (a définition et de comment t'en servir) t'a été dit dès le début. Donc actuellement, tu perds ton temps ...