Phase déroulée (unwrap phase)

[stefjm]

Bonjour,
C'est ma journée mathématique.
Est-ce que la notion de phase déroulée (unwrap phase) fait sens en mathématique?
Il me manque les mots clefs pour me débrouiller tout seul.

L'interrogation m'est venu à propos de l'argument de la fonction de transfert
L'argument en question varie de à

Voir ici pour le tracé de la phase en fonction de la fréquence.

Une discussion sur ce thème a lieu en physique pour les aspects physiques.
http://forums.futura-sciences.com/ph...-physique.html

J'espère comprendre ici les aspects mathématiques du truc.

Cordialement.
-----

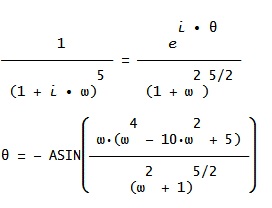
[stefjm]

Bonsoir,
Existe-il un lien compréhensible par un novice de mon genre entre

- le degré 5 de cette fonction de transfert qui fait faire plus qu'un tour à l'argument (-5pi/2)

et

- la non résolution par radicaux des polynômes de degré 5

?

Merci pour vos lumières niveau gentil pour ne pas me perdre...
Cordialement.

Edit : J'ai vu que Galois était le mot clef qui va bien mais j'avoue n'avoir pas compris grand chose.

[gg0]

Bonjour.

A priori non. D'ailleurs ici, tu n'as pas de polynôme.

[stefjm]

On peut prendre la fonction de transfert inverse. Elle est beaucoup moins physique, mais comme ici, c'est mathématique, on s'en fou...
La coïncidence du saut de phase à partir de l'ordre 5 m'a intrigué.
Et vu que je suis très loin du niveau en math qu'il doit falloir pour vérifier le point, j'appelle "au secours".

[A voir en vidéo sur Futura]

[polf]

En écrivant la fonction de transfert en séparant Amplitude et Phase :



Tu devrais reconnaitre les graphes de phase et d'amplitude.

[Médiat]

Bonjour,

Je ne comprends pas vraiment la question, mais en tout état de cause, quand je vois une équation de la forme x = arcsin(y), qui n'a qu'une seule solution en x (pour -1<=y<=1), je me dis qu'elle vient sans doute de l'équation y = sin(x) qui a une infinité de solution en x (pour -1<=y<=1), et qu'il y a, sans doute, des considérations physiques à prendre en compte.

[stefjm]

Bonjour Médiat,
IL est question ici de l'argument d'un nombre complexe toujours modulo en math, donc libre à .
Or selon les domaine de la physique (en général, en incluant les méchants techniciens ingénieurs), la "réalité" de l'argument n'est pas traitée de la même façon.
En gros, les considérations physiques sont variables, voir au pire vaseuses...

Parfois, il est considéré que l'argument doit être continu en fonction du temps (ou de la fréquence) et il est donc malvenu de se prendre des sauts de 2pi intempestifs : le technicien physicien les supprime. C'est la notion de unwrap phase, phase déroulée.

Parfois, il est considéré que l'argument est à 2pi près parce que la phase, c'est pas physique et donc on la choisit principale, comme en math.

Étant donné que les deux écoles de physicien ont raison toutes les deux dans leur domaine d'application, je me demandais s'il y avait une formulation propre en math pour la notion de phase déroulée.

Cordialement.

[gg0]

Bonjour Stefjm.

Tu aurais dû commencer par ce message, on aurait su quelle est ta question. Là c'est clair : les deux pratiques existent en maths, la première (modulo 2Pi) correspond à l'utilisation du cercle trigo mathématisée en , la deuxième correspond à ce qu'on appelle dans le cas général les surfaces de Riemann et dans le cas particulier à des relèvements sur le cercle.
D'autres ici en parleront mieux que moi (Mipama ? Médiat ? ...).

Pour la question de l'équation du cinquième degré, si la seule chose qui te fait mettre un rapport est le nombre 5, tu aurais dû aussi regarder les pentagones, l'impossibilité d'avoir un polyèdre régulier à 5 faces et tout ce qui s'exprime avec le chiffre ou le nombre 5.

Cordialement.

[stefjm]

Tu aurais dû commencer par ce message, on aurait su quelle est ta question. Là c'est clair : les deux pratiques existent en maths, la première (modulo 2Pi) correspond à l'utilisation du cercle trigo mathématisée en , la deuxième correspond à ce qu'on appelle dans le cas général les surfaces de Riemann et dans le cas particulier à des relèvements sur le cercle.

Merci. Je vais chercher avec ces informations.
J'ai l'impression qu'il y a donc deux mondes :
Fourier : on perd les tours : (i.w)^4=w^4
Laplace : on garde les tours. : p^4=p^4

Pour la question de l'équation du cinquième degré, si la seule chose qui te fait mettre un rapport est le nombre 5, tu aurais dû aussi regarder les pentagones, l'impossibilité d'avoir un polyèdre régulier à 5 faces et tout ce qui s'exprime avec le chiffre ou le nombre 5.

C'est un 5 lié au 2pi de ce sujet..
C'est la première valeur de k, telle que
k.pi/2>2pi

C'est lié aux intégrations qui retardent les signaux e^(ix) de pi/2, intégration qui donne 1/p en transformée de Laplace.

Il y a un rapport entre les surfaces de Riemann et Galois?

Cordialement.

[gg0]

Tu n'as pas encore d'autres idées de relations ?
En maths, tout à relation avec tout, il suffit de passer par les fondements, et on arrivera à mettre un lien. Mais ce n'est pas en se demandant si ceci a un lien avec cela qu'on apprend. C'est en étudiant vraiment chacun des éléments dont on a besoin. Et en évitant de se poser des questions oiseuses ("C'est un 5 lié au 2pi de ce sujet.").

Là, tu joue avec les mots. Aucun intérêt.

Désolé !

[stefjm]

Je ne m'intéresse aux maths que pour ce qu'elle m'apporte dans mon métier.
Si se poser des questions que j'estime intéressante, sinon, je ne les poserais pas, est considéré comme oiseux, ben ma foi, je ferai avec.

Je vais tâcher de comprendre le lien avec Galois.

[gg0]

Que c'est contradictoire !

Si tu ne t'intéresses pas aux maths en tant que telles, chercher des liens entre des théories ou notions qui ont été évoquées et d'autres que tu connais n'a aucun intérêt.

Tu donnes l'impression de prendre des mots du vocabulaire mathématique au hasard et de poser la question "intéressante pour toi" "est-ce qu'il y a un lien ?"
Et quand on te donne un vrai renseignement, tu le transformes tout de suite (tu es passé de mon indication à Fourier/Laplace sans même être allé voir de quoi je parlais) en des mots que tu connais.

Ciao !

[stefjm]

Bonjour,

Que c'est contradictoire !
Si tu ne t'intéresses pas aux maths en tant que telles, chercher des liens entre des théories ou notions qui ont été évoquées et d'autres que tu connais n'a aucun intérêt.

Je me sers des maths comme outils et suis capable de m'en servir sans rien comprendre, parce que d'autres ont bien bosser avant moi et on sait que cela marche dans tel domaine.
Parfois, je m'intéresse à l'origine des trucs que j'utilise, en particulier quand apparaissent des contradictions entre différents usages de ces trucs.
En gros, je suis un comptable qui s'intéresserait à la notion de retenue ou d'empreint qu'il utilise tous les jours parce que cela marche mais sans savoir pourquoi.

Tu donnes l'impression de prendre des mots du vocabulaire mathématique au hasard et de poser la question "intéressante pour toi" "est-ce qu'il y a un lien ?"
Et quand on te donne un vrai renseignement, tu le transformes tout de suite (tu es passé de mon indication à Fourier/Laplace sans même être allé voir de quoi je parlais) en des mots que tu connais.

Je suis désolé de donner cette impression.
Je suis en train d'essayer de comprendre les liens que tu m'as permis de trouver :
R/Z :
http://en.wikipedia.org/wiki/Quotient_ring
http://en.wikipedia.org/wiki/Quotient_group

Relèvement de Cercle :
http://fr.wikipedia.org/wiki/Revêtement_(mathématiques)
http://en.wikipedia.org/wiki/Covering_space

Et des trucs que j'utilise sans comprendre...
http://en.wikipedia.org/wiki/Quadrat...ude_modulation

Ciao !

Lorsque je découvre quelque chose que je ne connais pas, je dis ce que cela m'évoque pour que mon interlocuteur puisse avoir un retour rapide de comment est perçu ce qu'il a donné. J'essaie de voir le coté positif et de tout prendre. (y compris le 5 du pentagone et le fait que 6 soit le premiers entier inférieur à pour l'hexagone.)

Evidement, si tout a un rapport avec tout, ce n'est pas intéressant.
Mais pas plus pas moins que rien n'a de rapport avec rien.

Je t'accordes que le juste milieu à trouver n'est pas facile, ni pour toi, ni pour moi.

En tout cas, merci pour les mots clefs et sur ce, j'arrête de troller...

Cordialement.

[stefjm]

Pense bête personnel qui peut servir à d'autres.
http://www.latp.univ-mrs.fr/~mohsen/topo006.pdf

[azizovsky]

Salut, soit la fonction , le développement en série de Fourier sur , donne et , le représentation graphique de la série représente des discontinuité (sauts) en , comment reconstituer le fonction , à partir de sa réprésentation en série de fourier ?, je crois que c'est le noeud du problème .(''la fonction déroulée"")
en réalité la fonction ne représente aucune discontinuité .

[invite02232301]

Bonjour,

Tu donnes l'impression de prendre des mots du vocabulaire mathématique au hasard et de poser la question "intéressante pour toi" "est-ce qu'il y a un lien ?"

Ca donne vraiment cette impression, oui.

Néanmoins, si j'essaie de donner un sens à la question, j'ai l'impression que la question est juste celle du "relèvement" des applications de R (ici w est bien un réel, j'imagine) dans le cercle. Et la réponse est donnée par le theoreme du relevement.

Si on a un application de classe C^k (pour k entre 0 et omega, ou etre de classe C^omega c'est etre analytique réel) de R dans S^1, il existe un relevement de l'application dans R de meme classe, i.e une application g de R dans R telle que f=exp (2i\pi.g). Bien sur g n'est définie qu'a un multiple de 2\pi pres mais si on impose que les applications soient pointées i.e on choisit ce qu'on appelle un point base dans le cercle et dans R (c'est en general 1 pour le cercle si on voit le cercle comme les complexes de module 1, et 0 pour R) et l'on impose que les application f et g respectent ce point base i.e f(0)=1, et g(0)=0; ce qui correspond à ce que Stefjm appelle choisir une origine des phases; alors à ce moment là g est uniquement définie.
Ce theoreme se generalise vastement dans le cadre de la theorie des revetements.

Il y a un lien de la theorie des revetements avec la theorie de Galois, mais qui n'est pas du tout lié avec la puissance 5 ou quoi que ce soit, d'ailleurs je ne comprend pas quel est la nature du lien que Stefjm semble vouloir explorer (j'espere que c'est pas juste y a un 5 dans mon expression et la theorie de Galois dit qqch de special sur les polynomes de degré 5).
La theorie de Galois et la theorie des revetement admettent en fait une generalisation commune (et au sein de cette generalisation la theorie de Galois apparait essentiellement comme la theorie des revetements du point (ou plutot des points)).

[invite02232301]

En fait en lisant plus en details la discussion en physique ici, ce qui t'interesse c'est vraiment le theo du relevement. Si tu cherche une application continue de R dans R qui releve l'argument de ton truc, alors il n'est défini qu'à un multiple global de 2\pi pres (autrement dit si tu te donnes deux fonctions g et h qui sont des "arguments" de ta fonction de transfert, alors il existe un k entier , tel h=g+2k\pi (parce que h-g est continue de R dans 2\pi.Z, donc constante), si tu fixes une origine, alors k=0, et ton "argument" est entierement determiné).

Je mets des guillemets à argument car l'argument d'un nombre complexe c'est un element de R/Z, pas de R, ici tu veux un réel, pas un reel module 2\pi.

[azizovsky]

Salut, si j'ai 'roulé' une fonction(mon fil)sur un cercle càd Chaque fibre est ici infinie dénombrable, la fonction de déroulement du fil ,tu peut regarder le lien que j'ai donné sur l'autre discussion ou http://fr.wikipedia.org/wiki/Rev%C3%...C3%A9matiques), je peut enroulé mon fil sur un cylinde,un tore..,mais pour déroulé ....

[stefjm]

Salut, soit la fonction , le développement en série de Fourier sur , donne et , le représentation graphique de la série représente des discontinuité (sauts) en , comment reconstituer le fonction , à partir de sa réprésentation en série de fourier ?, je crois que c'est le noeud du problème .(''la fonction déroulée"")
en réalité la fonction ne représente aucune discontinuité .

Oui, c'est une façon de poser le problème.
D'un coté Yd=x et de l'autre par exemple)
Ce que confirme proprement gg0 et MiPaMa.

Néanmoins, si j'essaie de donner un sens à la question, j'ai l'impression que la question est juste celle du "relèvement" des applications de R (ici w est bien un réel, j'imagine) dans le cercle. Et la réponse est donnée par le theoreme du relevement.

Oui, w est réel.

Si on a un application de classe C^k (pour k entre 0 et omega, ou etre de classe C^omega c'est etre analytique réel) de R dans S^1, il existe un relevement de l'application dans R de meme classe, i.e une application g de R dans R telle que f=exp (2i\pi.g). Bien sur g n'est définie qu'a un multiple de 2\pi pres mais si on impose que les applications soient pointées i.e on choisit ce qu'on appelle un point base dans le cercle et dans R (c'est en general 1 pour le cercle si on voit le cercle comme les complexes de module 1, et 0 pour R) et l'on impose que les application f et g respectent ce point base i.e f(0)=1, et g(0)=0; ce qui correspond à ce que Stefjm appelle choisir une origine des phases; alors à ce moment là g est uniquement définie.
Ce theoreme se generalise vastement dans le cadre de la theorie des revetements.

Merci à toi et gg0.
La notion de pointage nécessaire ou pas sera à rapprocher de considération physique.

Il y a un lien de la theorie des revetements avec la theorie de Galois, mais qui n'est pas du tout lié avec la puissance 5 ou quoi que ce soit, d'ailleurs je ne comprend pas quel est la nature du lien que Stefjm semble vouloir explorer (j'espere que c'est pas juste y a un 5 dans mon expression et la theorie de Galois dit qqch de special sur les polynomes de degré 5).
La theorie de Galois et la theorie des revetement admettent en fait une generalisation commune (et au sein de cette generalisation la theorie de Galois apparait essentiellement comme la theorie des revetements du point (ou plutot des points)).

Il y a un peu plus que cela.
Cela concerne la stabilité des systèmes linéaires et leur stabilisation par contre réaction en commande de procédé.
Je travaille en Laplace, variable p ou Fourier i.w.
On regarde la stabilité des systèmes en boucle fermée grâce à la représentation dans le plan complexe de BO/(1+B0) par rapport au point -1 du plan complexe.

Les systèmes d'ordre 1 sont inconditionnellement stable (si on ne merde pas le signe, toujours le soucis des réels négatifs). On dit qu'ils ont une marge de phase supérieur à 90° et de marge de gain infinie.
Ordre 1 : On passe très loin du point critique -1. cf graph de Nichol.
Le pôle est réel, si négatif, c'est stable.
Pas besoin de stabilisation.

Les systèmes d'ordre 2 sont encore inconditionnellement stable, mais leur marge de phase peut se réduire à 0.
Ordre 2 : On peut passer tout près de -1.
Les pôles sont alors complexes conjugués, système stable si la partie réelle est négative et exprimable analytiquement avec des radicaux.
Facile à stabiliser en "rattrapant" 90° de phase.

Les systèmes d'ordre 3 peuvent être instables car le déphasage dépasse -180°. (jusqu'à -270°)
On peut les stabiliser en rattrapant 90° de phase.
Les physiciens les trouvent non physique avec des défauts soit de causalité, soit de stabilité. (Et personne ne se met d'accord proprement sur les caractéristiques.)

Les systèmes d'ordre 4 sont encore stabilisable et on peut trouver des solutions analytiques. Ils ont une phase de -360° au pire, ce qui les fait ressembler au système instantané d'ordre 0. (pas de déphasage)
Les systèmes électromécanique sont d'ordre 4. (2 pour l'électricité, 2 pour la mécanique)

A partir de l'ordre 5, il y a une retenue 2pi sur la phase. et plus de solution sous forme de radicaux pour les pôles.

Cordialement.

PS : Je n'ai pas tout traduit proprement en maths, j'espère que c'est assez clair.

[azizovsky]

Salut, le problème est lié au codage d'une fonction (en série de fourie ou laplace ou ...) et son décodage.

je crois que la stabilité d'un système est un autre problème plus comliqué..

[stefjm]

En fait en lisant plus en details la discussion en physique ici, ce qui t'interesse c'est vraiment le theo du relevement. Si tu cherche une application continue de R dans R qui releve l'argument de ton truc, alors il n'est défini qu'à un multiple global de 2\pi pres (autrement dit si tu te donnes deux fonctions g et h qui sont des "arguments" de ta fonction de transfert, alors il existe un k entier , tel h=g+2k\pi (parce que h-g est continue de R dans 2\pi.Z, donc constante), si tu fixes une origine, alors k=0, et ton "argument" est entierement determiné).

Je mets des guillemets à argument car l'argument d'un nombre complexe c'est un element de R/Z, pas de R, ici tu veux un réel, pas un reel module 2\pi.

Merci MiPaMa et gg0.
30 ans que je joue avec les complexes en maths, physique, électronique, automatique, etc... et c'est la première fois que j'entends parler de cela!
Ca éclaire pas mal de chose.

Salut, si j'ai 'roulé' une fonction(mon fil)sur un cercle càd Chaque fibre est ici infinie dénombrable, la fonction de déroulement du fil ,tu peut regarder le lien que j'ai donné sur l'autre discussion ou http://fr.wikipedia.org/wiki/Rev%C3%...C3%A9matiques), je peut enroulé mon fil sur un cylinde,un tore..,mais pour déroulé ....

L'autre lien, j'ai un peu de mal à suivre et voir de quoi il est question, même dans les très grandes lignes.

Cordialement.

[invite02232301]

Il y a un peu plus que cela.
Cela concerne la stabilité des systèmes linéaires et leur stabilisation par contre réaction en commande de procédé.
Je travaille en Laplace, variable p ou Fourier i.w.
(...)
PS : Je n'ai pas tout traduit proprement en maths, j'espère que c'est assez clair.

Rien compris. Je ne connais pas la définition de plus de la moitié des termes que tu utilises.

[stefjm]

Avec les mains :
Une fonction de transfert d'ordre 2 a sa phase qui varie de -pi (au plus). A haute fréquence, c'est comme une multiplication par -1. (au gain près, mais ici, on ne parle que de phase.) Du coup, certain considèrent la phase à pi près.
Une fonction de transfert d'ordre 4 a sa phase qui varie de -2pi (au plus), soit un tour complet. A haute fréquence, c'est comme une multiplication par 1. (au gain près) Et du coup, certains considèrent qu'il n'y a plus de déphasage.

Pour ces ordres là, on trouve des solutions en radicaux pour les pôles.

A partir de l'ordre 5...

[invite02232301]

Bon, j'ai du temps, je persevere,

Avec les mains :
Une fonction de transfert d'ordre 2 a sa phase qui varie de -pi (au plus).

Qu'est ce qu'une fonction de transfert? J'imagine que c'est une fonction de R dans C (associée à un systeme physique j'imagine).
Qu'est ce que c'est l'ordre d'une fonction de transfert, j'ai l'impression qu'une fonction de transfert d'apres tes exemples, c'est une fraction rationnelle à coeff complexe, c'est le degré de son dénominateur (sous forme irreductible)?

A haute fréquence, c'est comme une multiplication par -1. (au gain près, mais ici, on ne parle que de phase.)

Qu'est ce "qui est comme une multiplication par -1"? Désolé mais pour moi "une fonction est comme une multiplication par -1"... je ne vois pas ce que ca peut vouloir dire.

Une fonction de transfert d'ordre 4 a sa phase qui varie de -2pi (au plus), soit un tour complet. A haute fréquence, c'est comme une multiplication par 1. (au gain près)

Meme remarque.

Pour ces ordres là, on trouve des solutions en radicaux pour les pôles.

A partir de l'ordre 5...

Et donc?

[stefjm]

Qu'est ce qu'une fonction de transfert? J'imagine que c'est une fonction de R dans C (associée à un systeme physique j'imagine).
Qu'est ce que c'est l'ordre d'une fonction de transfert, j'ai l'impression qu'une fonction de transfert d'apres tes exemples, c'est une fraction rationnelle à coeff complexe, c'est le degré de son dénominateur (sous forme irreductible)?

Oui.
La plus simple, c'est 1/(i.w) en Fourier ou 1/p en Laplace. C'est une intégration temporelle.
Sa phase vaut -90°

Qu'est ce "qui est comme une multiplication par -1"? Désolé mais pour moi "une fonction est comme une multiplication par -1"... je ne vois pas ce que ca peut vouloir dire.

La fonction de transfert change le signe entre entrée et sortie.
Par exemple 1/(i.w)^2 ou 1/p^2, de phase -180°. Une double intégration temporelle.
-1=1.e^(i.180°)

Meme remarque.

1/(i.w)^4 ou1/p^4, de phase -360°. Une quadruple intégration temporelle.
1=1.e^(i.360°)

Et donc?

A partir du degré 5, terre inconnue pour moi.
Cordialement.

[invite02232301]

La fonction de transfert change le signe entre entrée et sortie.
Par exemple 1/(i.w)^2 ou 1/p^2, de phase -180°. Une double intégration temporelle.
-1=1.e^(i.180°)

Mais... ca n'a rien à voir avec le fait que ta fonction de transfert soit "d'ordre 2"... est aussi de phase -\pi, hein, pour tout n.

[invite02232301]

Arff, est aussi de phase -\pi/2, hein, pour tout n.
Et, je ne comprend toujours pas quelle est la question...

[invite02232301]

La seule interpretation que j'arrive à donner a ton discours est la suivante.
On suppose qu'on se donne une EDO sur R, i.e on cherche à résoudre qqch du genre pour a_i des fonctions lisses disons.
Sous de bonnes conditions de regularité il existe un opérateur T de L^2 dans L^2 tel que l'equation soit équivalente à T(F(x))=0 ou F(x) est la transformée de Fourier (ou de Laplace) de x. Parfois, par exemple quand le systeme est à coeff constant, T est simplement un opérateur de multiplication par une fonction de L². Si c'est le cas on va l'appeler la fonction de transfert de l'EDO.
Si T est une fraction rationnelle peut on relier les propriétés de T, notament le degré de son dénominateur à.... A quoi exactement? Je ne sais pas.
Au fait que la transformée de Fourier inverse est calculable? Dans ce cas là faut regarder du coté de la théorie de Galois differentielle.
A autre chose? A la stabilité du systeme dynamique? C'est vraiment pas la peine pour un systeme à coeff constant, on sait en examinant simplement la mtrice compagnon du systeme si le systeme est stable ou pas, voir le critère de Routh voir ici, par exemple
A encore autre chose? Mais quoi?

[azizovsky]

Salut, comme je l'ai dit avant, le problème ou théorie de la stabilité est un domaine plus vaste ..., il y'a beaucoup de sorte de stabilité pour un système , stabilité selon : Lagrange-Dirichlet, Poission-Ponicaré, Lyaunov, et critères : de Routh-Hurwiz,géométrique de Mikhaïlov....
http://fr.wikipedia.org/wiki/Stabili...v#Lyapunov1992