Limite supérieure et inférieure

[invite2bef55d1]

Bonjour à tous,

je sais que ma compréhension laisse à désirer concernant ces notions donc je viens demander de l'aide...
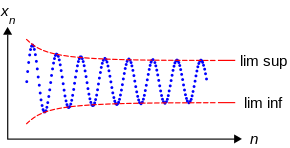
J'ai très bien compris pourquoi (sup {Uk; k>n})n>0 est decroissante minorée dans ce cas:


Cependant, j'ai appris que cette suite étais décroissante minorée dans tous les cas quand Un est bornée en valeur absolue.
Aidez moi à comprendre comment cela est possible par exemple avec Un = 1 - 1/n
Un est minorée par 0 et majorée par 1. Mais je n'arrive pas du tout à visualiser la suite (sup {Uk; k>n})n>0 dans un tel cas...

Merci beaucoup !
-----

[gg0]

Bonjour.

Pourtant, tu sais calculer sup {Uk; k>n}. Ça fait ... et la suite des (...)n est bien décroissante, et minorée par 0 comme Un.

Cordialement.

Rappel : Une suite constante est et croissante, et décroissante.

[invite2bef55d1]

Si j'ai bien compris, comme Un = 1 - 1/n est stationnaire (mais peut on le dire dans ce cas ?), elle n'admet qu'une seule valeur de sup {Uk; k>n} = 1 ici donc décroissante minorée etc... ?

J'ai juste besoin de la confirmation !

[gg0]

Je ne vois pas pourquoi tu parles de stationnaire pour U : Elle est strictement croissante. Par contre, comme elle est majorée, elle a une limite, son sup. La suite des sup est elle, stationnaire, et même constante (stationnaire = constante à partir d'un certain rang).

En fait, si tu avais vu ça, il te suffisait d'appliquer les règles. Comme toi, je n'ai pas d'autre moyen de savoir ce qui est juste.

Cordialement.

[A voir en vidéo sur Futura]

[invite2bef55d1]

Ah d'accord, mais ca veut dire que par exemple si on prend U2 qui vaut 1/2, pourquoi a-t-on sup U2 = 1 et n'a-t-on pas sup U2 = 1/2 ?
Faut-il prendre en compte l'ensemble de la suite à chaque fois ou peut-on déterminer le sup point par point ?
(parce qu'en fait en le déterminant point par point on en déduit que sup {Uk; k>n} est croissante... Contradictoire avec la définition)

[gg0]

As-tu lu la définition ?

Il n'y a pas de sup U2.
Dans (sup {Uk; k>n})n>0, comme l'indice est n, on a la suite sup {Uk; k>1},sup {Uk; k>2},sup {Uk; k>3},sup {Uk; k>4},...

Manifestement, contrairement à ce que tu disais, tu n'avais pas du tout compris.

Cordialement.

[invite2bef55d1]

Ah en effet, ce k me posait probleme (je ne voyais que dans un seul cas).
D'accord, donc dans ce cas on a sup {Uk; k>1} = sup {Uk; k>2} = sup {Uk; k>3} = sup {Uk; k>4} etc... d'où sup Uk, k>n est stationnaire ici et vaut 1
Merci !

Cordialement