Recherche de l'équation polaire d'une courbe

[invite748a7e91]

Je compte sur l'aide de l'un ou l'autre et si quelqu'un sait où je peux en trouver qu'il n'hésite pas à m'en informer car ce problème est quelque peu coriace !

Le problème consiste à déterminer l'équation (polaire) de la courbe effectuée par l'extrémité "M" d'un rayon vecteur dont la longueur est fonction d'un paramètre, cette courbe étant tracée sur un plan.

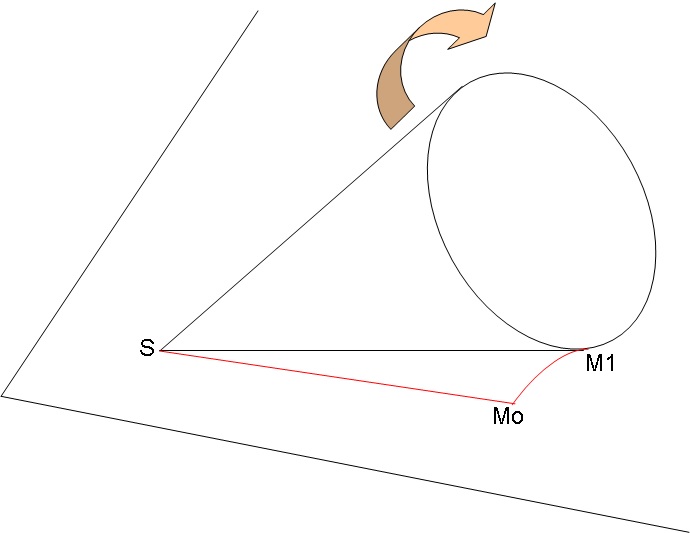
On connaît deux points : S (-xo, 0, h) et M (rsinα, rcosα, 0),

On sait déterminer le module de SM en fonction de α, soit f(α) ainsi que la longueur du chemin parcouru par M en fonction de α soit g(α) ; en l'occurrence g(α) = rα.

A partir des deux fonctions f(α) et g(α) on peut tracer SMo pour α=0 puis, de proche en proche SM1 avec MoM1 = rα1, puis SM2 avec M1M2 = r(α2-α1) et ainsi de suite jusqu'à ce que le point "M" ait fait un tour complet...

Ma question : Comment déterminer l'équation polaire d'une telle courbe (la solution sera du genre intégrale elliptique mais ce n'est pas dérangeant). Attention, je ne demande pas quelle est la longueur de cette courbe, ce n'est pas d'une intégrale curviligne dont j'ai besoin d'ailleurs je connais déjà cette longueur : c'est rα. M'est avis que le raisonnement doit s'approcher du processus permettant d'établir la courbe du chien (voir Wikipédia)

Par avance merci !
-----

[gg0]

Bonjour.

Ton exposé est loin d'être clair ! J'ai passé plus de 5 mn avant de commencer à avoir une idée, peut-être fausse. Faut-il comprendre que M est dans le plan z=0 ? D'autre part, la longueur du chemin parcouru ne suffit pas à placer le point M1 : Il y a tout un cercle de points situés à la distance M1M2 = r(α2-α1) de M1. Donc tu as sans doute une autre condition.

Cordialement.

NB : un croquis serait sans doute utile.

[invite748a7e91]

Merci de t'intéresser à ce problème. Il s'agit en fait d'un cône dont le sommet est S (-xo, 0, h) et la base un cercle dans le plan X0Y centré sur l'origine dont un point courant "M" est défini par les coordonnées rsinα, rcosα, 0.

Le problème consiste à déterminer la courbe d'équation du développement du cône ou encore la courbe décrite pat le point "M" si l'on fait rouler le cône sans glisser sur un plan.

Est-ce plus clair ?

Cordialement

[invite748a7e91]

Voici un schéma de la courbe recherchée :

[A voir en vidéo sur Futura]

[gg0]

Désolé, c'est toujours incompréhensible !
Tu n'as pas dit sur quel plan tu fais rouler le cone (ce ne peut pas être son plan de base); ni comment il roule.

[invite820993ca]

Ah je crois qu'il cherche l'équation de la cycloïde. Wikipédia vous la donne en un clic.

[azizovsky]

il y'a des cas plus compliquer : http://www.mathcurve.com/courbes3d/c...dspheric.shtml, je crois c'est ça sur ub plan.

[invite748a7e91]

En fait imaginez qu'on prenne le cône à pleine main et qu'on le face rouler sur un plan ; qu'elle est l'équation de la courbe décrite par le point "M" ou encore qu'elle est l'équation du développement. La difficulté du problème vient du fait que l'on ne connaît que 2 choses :

1) la longueur de SM, et

2) La longueur du chemin parcouru par le point "M".

Je pense que la résolution du problème passe par un équation différentielle du second ordre...

Cordialement

[invite820993ca]

C'est définitivement l'équation d'une cycloïde. Qu'elle soit sphérique ou dans le plan difficile de savoir avec des explications du genre: "prendre le cône à pleine main".

Les équations différentiel c'est plutôt en physique au cas où.

[gg0]

Un cône qui roule sur un plan, enfin je suppose qu'il s'agit de son cercle de base, peut suivre n'importe quel tracé (voir les appareils pour mesurer les distances sur les cartes). Donc on est ici face à une question que le questionneur ne connaît pas vraiment, qui a des réponses pour lesquels les répondeurs sont amenés à imaginer des interprétations !!

F6eyo, quand tu auras vraiment compris de quoi tu veux parler, tu le traduiras clairement. Pour l'instant, tu n'as jamais été capable de dire même sur quel plan roule le cône !! Celui du message #3.

En attendant qu'il y ait un énoncé de question sérieux, je laisse tomber.

[invite748a7e91]

ça me paraissait simple pourtant d'imaginer un cône qui roule sans glisser sur un plan.
Est-ce qu'avec cette figure ça rend plus simple la représentation du cône et du plan ?

[invite820993ca]

Êtes vous au moins passer voir si la cycloïde répondait à votre problème ?

C'est desagreable de parler à quelqun qui ne connaît pas son sujet. Comment peut on vous aider si l'on ne peut pas communiquer ?

[invite748a7e91]

Non, la cycloïde ne répond pas à ce problème.

La difficulté vient du fait que, pour rechercher l'équation de la courbe décrite par le point "M", on ne connaît que la longueur du rayon (le segment SM) dont le module est une fonction d'un paramètre (appelons le α) et de la longueur du chemin parcouru par l'extrémité du rayon (la longueur MoM1 dans la figure du message No5). Avez-vous bien saisi le problème ?

Cordialement

[gg0]

Bonjour.

Avec ce schéma, qui ne correspond pas à ce que tu disais au message #1, on sait quel est le vrai problème. Et quel est le plan à considérer. La courbe qui t'intéresse peut être décrite en polaire sous une forme r=f(t) en prenant comme origine dans le plan le point S et comme axe polaire la directrice du demi-cône en contact avec le plan au moment où le cône commence à rouler. Ensuite, il va falloir déterminer quel est l'angle polaire quand le cône tourne sur lui même d'un certain angle. Comme il y a proportionnalité, c'est un calcul simple où le rapport ne dépend que de l'angle au sommet du cône. On le calcule pour un cône droit de même angle. Enfin il faut modéliser la longueur de la directrice du demi-cône en contact avec le plan en fonction de l'angle dont à tourné le cône. C'est de la géométrie élémentaire.

Dans tout ça, pas d'équation différentielle, seulement de la géométrie élémentaire (angles, longueurs, trigo, ...). Pour un cône droit, la courbe est un cercle, pour un cône oblique, ça ressemble à une épicycloïde; mais il est peu probable que c'en soit une.

Commence à calculer, moi je n'ai pas le temps ce matin.

Cordialement.

[invite748a7e91]

Je crois qu'on a du mal à se comprendre... Le problème est posé dès le message No 1 que je résume comme suit : Rechercher l'équation de la courbe polaire qui est définie par un rayon "SM" de module variable fonction d'un paramètre "α" qui tourne autour de son origine "O" dont on ne connaît pas l'angle de déplacement mais seulement la longueur du chemin parcourue par son extrémité "M"...

Le problème se résout facilement par graphique. Il suffit de prendre des arcs du cercle de base suffisamment petits pour les assimiler à des segments de droite pour approximer la courbe polaire de proche en proche comme sur la figure ci jointe.

Toute la difficulté réside dans le fait que l'on n'a que deux fonctions à sa disposition ; celle qui régit le module du rayon et celle qui régit la longueur du chemin entre deux points "M" consécutifs.

Déterminer le premier point de construction de la courbe ne pose pas de problème, c'est l'extrémité du segment "SM" pour la 1ère valeur du paramètre, disons pour α=0.

Ça se complique quand on veut déterminer un second point, disons quand α= π/12 par exemple. On détermine bien le module de "SM" et la longueur du chemin parcouru par le point "M" pour α= π/12 mais comme on ne connaît pas la forme du chemin parcouru par l'extrémité de "SM" on est incapable de placer correctement le segment "SM". L'idée, et tu as mis le doigt dessus, serait d'établir l'équation qui donne l'angle entre vecteurs mais chercher à établir cette équation ou celle de la courbe relève de la même difficulté. Comme je l'ai annoncé dès le début, c'est un problème coriace, ça ne se résout pas d'une pichenette ! 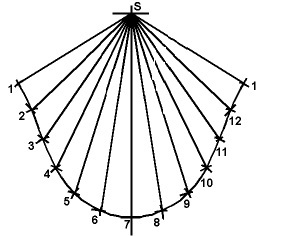Et le plus amusant c'est que l'on connaît dès le début la longueur totale de la courbe, c'est 2πr...

[invite748a7e91]

Ces cas sont relativement simples car les épicycloïdes sont générées par un cône droit de révolution. Les équations se trouvent assez facilement. C'est autrement plus compliqué quand le cône n'est pas droit, qu'il roule sur un plan et que l'on veuille établir la courbe de la trajectoire de sa base...

Cordialement

[gg0]

Désolé,

mais je ne te comprends pas. le problème posé au message #1 n'a pas de solution : Il manque des éléments pour savoir comment on passe d'un premier point à un point proche. Le problème du cône, qu'il soit droit ou non, se traite facilement comme je te l'ai proposé (un cône oblique roule exactement comme un cône droit, sauf que le point de la base qui touche le plan se situe à une distance variable du sommet).
Et contrairement à ce que tu dis, si c'est un cône droit, on obtient un cercle (*), pas une épicycloïde.

Donc tout est toujours très confus dans ce que tu racontes. On ne sait plus quel est le vrai problème. Si ce n'est pas le cône, n'en parles plus, mais définis clairement la problématique complète.

Cordialement.

(*) A moins que le sommet bouge, donc qu'il n'y ait plus seulement roulement du cône sur le plan.

[invite748a7e91]

Où ai-je écrit que le développement d'un cône droit était une épicycloïde, évidemment que c'est un cercle (en réalité c'est un secteur circulaire) ?

Quant à ce que tu écris concernant le cône oblique c'est parfaitement exacte, même que depuis le début de la discussion je cherche à en établir la courbe d'équation à partir des deux seuls éléments connus : f(α) et g(α)...

Ton idée d'angle au sommet m'en donne une... d'idée ! En creusant un peu je me dis que prendre le problème en commençant par établir l'équation de l'angle polaire (θ) en fonction du paramètre "α" me permettrait peut être d'arriver à mes fins car dans ce cas, l'équation différentielle est : dθ/dα = 1/g Racine (g'^2 - f'^2) !

Es-tu d'accord ?

Cordialement

[invite748a7e91]

Au fait, à propos de l'épicycloïde^... C'était une réponse au message #7, mais comme je suis nouveau sur ce forum j'ai cru que ma réponse se placerait sous son message. Je comprend la confusion générée.

Cordialement

[invite820993ca]

Pour vous aider, je pense qu'il serait plus judicieux et lisible de poser les chose comme ça:



en posant donc u(a)= f'(a) et w(a)= g'(a). C'est équivalent.

si vous connaissez f(a) et g(a) mais ça semble pas juste correspondre a votre problème...

[invite820993ca]

A moins que votre rayon A est constant.

[invite748a7e91]

Merci à Lyris. En cogitant un peu j'arrive à ceci :

A force de reformuler l’énoncé de mon problème dans tous les sens en espérant qu’il soit mieux compris (apparemment je n’y suis pas arrivé…) j’ai peut être trouvé une voie à suivre à partir du message #14, notamment l’idée de déterminer l’angle polaire dans et une autre façon d’énoncer le problème : <<- Un cône oblique roule exactement comme un cône droit, sauf que le point « M » de la base qui touche le plan se situe à une distance variable « SM » du sommet->>., le sommet étant bien sur fixe.

Pour tenter d’établir la courbe de la trajectoire du point « M » on dispose, de deux informations (voir #1)

1) Le module de « SM » en fonction de α, soit f(α), et

2) Longueur du chemin parcouru par « M » en fonction de « α » soit g(α)

Déterminer l’angle polaire à partir du paramètre « α » revient à résoudre l’équation différentielle suivante :

EquaDiffGen.jpg

Avec les définitions des points « S » et « M » données en #1, on définit f(α) et g(α):

Module de SM : f(α) = [ (rsinα + xo) 2 + (rcosα) 2 + h2] ½

Lg du chemin parcouru : g(α) = rα

Les dérivées de ces deux fonctions sont (je revérifierai) :

f’(α) = [((rsinα + xo) rcosα) -rcosα sinα ] / [ (rsinα + xo) 2 + (rcosα) 2 + h2] ½

g’(α) = r

L’équation différentielle à résoudre et donc :

EquaDiffTech.jpg

Comme je m’en doutais c’est bien d'une intégrale elliptique qu'il s'agit, mais je pourrai l'approximer en utilisant une méthode numérique (celle de Simpson par exemple) et tout ça pour trouver l’angle polaire en fonction de « α » : θ(α)… Je savais que cela aurait été aussi chiant que de déterminer la courbe mais je suis persuadé que c'est la façon la plus simple pour parvenir à un résultat.

Je ne suis pas encore au bout du bout mais pas bien loin de détenir les deux paramètres (surtout le premier) nécessaires et suffisants à définir ma courbe : θ(α) et f(α), restera ensuite à intégrer ça dans mon logiciel, de faire les vérification et puis c'est marre !

Merci à tous ceux qui se sont intéressés à ce petit problème quand même assez coriace voir rebutant !

Cordialement

[invite820993ca]

j'ai dit une bourde tout à l'heure, mais passons... Ca a l'air mieux énoncer je vais regarder après mes cours quand j'ai le temps.

[invite748a7e91]

J'ai l'impression que dθ et dα sont inversé dans #20 et pour #21 le rayon n'est pas constant et c'était bien là le problème... De toute façon pour la formule en #20 ce n'est pas d'une longueur de courbe (intégrale curviligne) dont on a besoin (on connaît déjà g(α).

Merci pour votre participation

Cordialement

[invite748a7e91]

Conclusion :

Pour celles ou ceux qui s'intéressent à ce sujet on peut résumer l'énoncé du problème comme suit :

On raisonne dans le plan. Déterminer l'angle polaire d'un rayon vecteur de longueur variable dont le module est une fonction de "α" [f(α)] et dont l'origine est fixe et l'autre extrémité parcourt un chemin de longueur elle aussi fonction de "α" [g(α)] (voir #1).

Vu les 24 messages de cette discussion dont pratiquement tous ne concernaient que la formulation de l'énoncé du problème en vue de pouvoir l'appréhender j'imagine sans peine qu'il faudra un peu beaucoup de temps pour y arriver.

Ceci dit la solution, en ce qui concerne la détermination de l'angle polaire, apparaît au message #22.

Je ne sais pas comment on clôture une discussion sur ce forum mais elle l'est !

[Médiat]

Bonjour,

Si je comprends votre énoncé, vous avez une relation entre la variation d'angle polaire et la variation de module (j'ai noté votre paramètre) :

[invite748a7e91]

Bonjour,

Disons que le module du rayon vecteur et l'angle polaire sont tout deux exprimés en fonction d'un paramètre "α".

En #22 on voit comment on peut exprimer la relation entre l'angle polaire et "α" (intégrale qui reste à approximer et où il y a une erreur que je corrigerai plus tard)...

Cordialement

[invite748a7e91]

Après vérification voici l'équation différentielle de #22 sans erreur et simplifiée :





Cordialement

[invite748a7e91]

Je me suis planté dans l'équa diff générale... ]

Après vérification l'expression de l'angle polaire "θ" en fonction du rayon vecteur SM= f(α) et de la longueur de courbe g(α) est EquaDiffGen.jpg

L'équation différentielle à "résoudre" est donc : EquaDiffTech.jpg...

Mille excuses !

Cordialement