Bonsoir,
je souhaite prouver cette propriété.
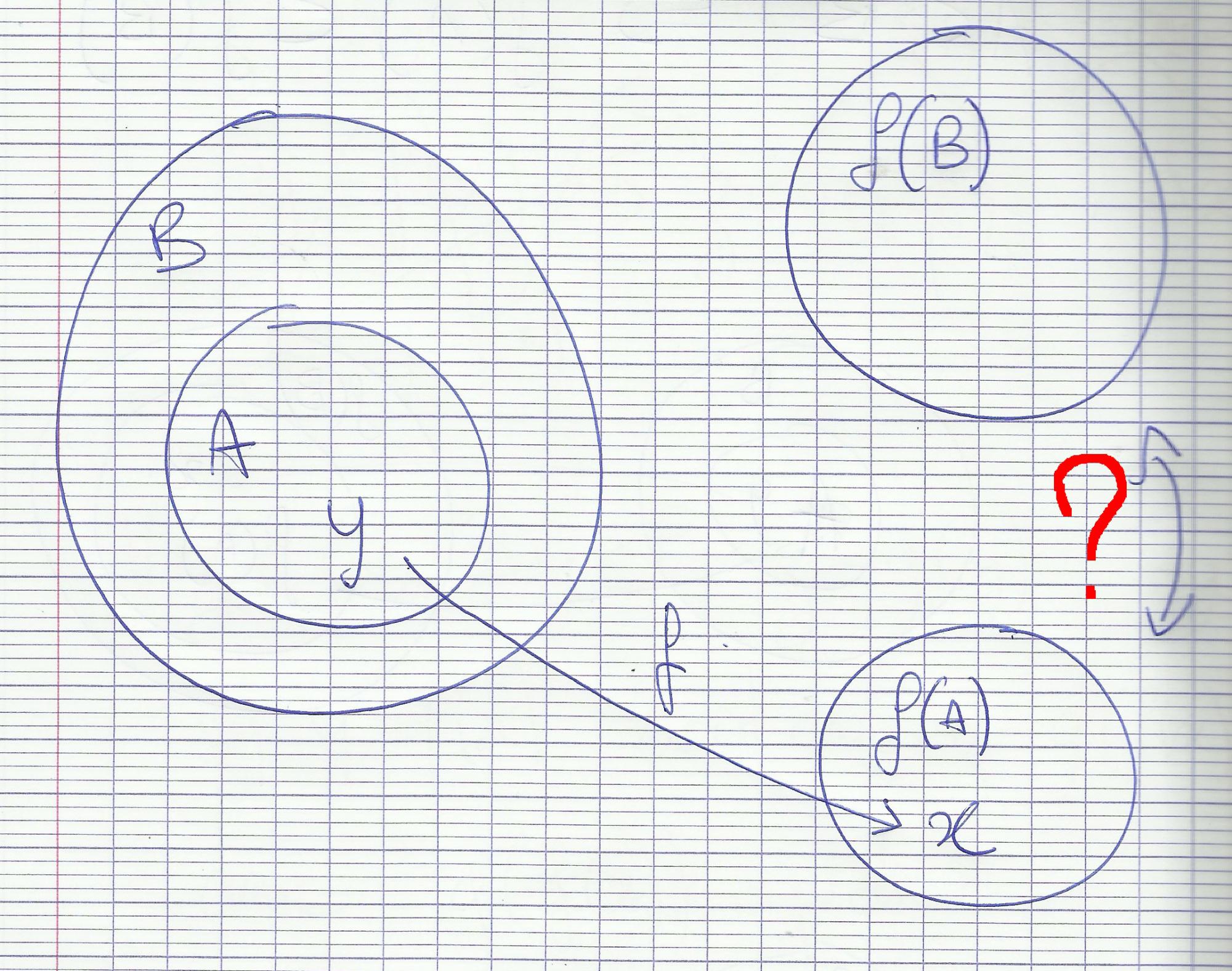
f est une application de E dans F Soit A et B deux sous ensembles de E tels que A inclus dans B donc pour tout x appartenant à A on a x appartient a B donc f(A)={pour tout y appartenant à F, il existe x appartenant a B tel que f(x)=y }=F inclus dans f(B).
Donc f(A) inclus dans f(B).
Ma démonstration est elle juste ?
Merci
Bonsoir ... ou bonjour,
Je ne trouve pas cette rédaction très limpide ... Rédige plutôt ta démonstration de la manière archi classique suivante :Envoyé par Jean-Luc97233
Soit. Tu traduis cela. Puis tu justifies pourquoi
Cordialement
Dernière modification par PlaneteF ; 16/05/2015 à 05h25.
Bonjour. Je veux me baser rigoureusement sur les définitions pour ma démo. Voila ce que j'obtiens :
Est ce bien cela ?
Cordialement
Ca tombe bien, c'est exactement ce que je te proposais dans mon précédent message
... Ben rebelote, ce n'est toujours pas limpide, peut-être encore moins que dans ton premier message
Ta dernière implication implique la définition de
Où montres-tu explicitement dans ce que tu écris qu'un élément de
--> Reprend ce que je t'ai proposé. C'est la rédaction standard et rigoureuse pour ce genre de démonstration.
Cdt
Dernière modification par PlaneteF ; 16/05/2015 à 17h40.
Donc concrètement la démonstration sera sur ce schéma :
Supposons
...
Bla bla bla ...
...
Donc
Donc
--> Reste plus qu'à rédiger le "bla bla bla ..." ...--> C'est très simple, c'est 2 lignes.
Cdt
Dernière modification par PlaneteF ; 16/05/2015 à 18h24.
Oui j'ai bien tenté de compléter ta démo initiale( mon y correspond a ton x ) mais je suis à coté de la plaque. Mon élément x appartient a A et B, y appartient a f(A). Comment y peut aussi appartenir à f(B) ? c'est çà le coeur du problème. l'implication que f(A) inclus dans f(B), n'est pas si évidente ( du moins pour moi
Comment tu arrives a faire des citations avec LaTex ?
Ben tu écris tout simplement ceci :
Supposons
Or
Donc ...
...
Ben je te laisse le soin de conclure, ... à partir de là c'est quasi fini !
Cdt
Dernière modification par PlaneteF ; 16/05/2015 à 19h05.
Tout cela je le sais bien. Soit il me manque une propriété, soit je passe toujours a coté mais le problème est comment montrer explicitement qu'un élément de f(A) est forcément élément de f(B) comme tu dis.
Et aussi comment peux tu faire des citations en utilisant les citations Latex de tes interlocuteurs ? je n'arrive qu'a citer le texte
cdt
M'enfin c'est terminé --> Puisque
Et donc par définition ce a veut dire que
Tu as des boutons en bas à droite de chaque message pour cela.Et aussi comment peux tu faire des citations en utilisant les citations Latex de tes interlocuteurs ? je n'arrive qu'a citer le texte
Cdt
Dernière modification par PlaneteF ; 16/05/2015 à 19h51.
Ben il m'a semblé avoir dit exactement la même chose mais formulé de manière bien plus lourde. En tout cas merci. C'était un vrai accouchement dans la douleur, mais je vais tenter de me baser sur ton formalisme plus léger.Bonjour. Je veux me baser rigoureusement sur les définitions pour ma démo. Voila ce que j'obtiens :
Est ce bien cela ?
Cordialement
cdt
Non, ... je ne vois pas le rapport avec ce que tu avais écrit, qui de surcroît ne démontrait rien du tout :
D'un point vue purement logique cette implication n'est pas fausse puisqu'elle est du type VRAI=>VRAI ... Mais elle sert à quoi
De la même manière l'implication (Paris est la capitale de la Norvège) => (2+2=5) est une implication VRAIE et comme ton implication en quoi cela prouve t-il que
Cdt
Dernière modification par PlaneteF ; 16/05/2015 à 22h59.
Désolé, je vois que j'ai la tête particulièrement dure. Merci d'avance pour ta patience.
J'ai repris la totalité de ta démonstration :
1)Supposons
2)on a
3)donc
4)donc
Si je n'ai rien oublié, en quoi l'égalité de la ligne 2) permet de déduire que x appartient à f(B) à la ligne suivante ?
Cdt
Bah c'est la définition de f(B), c'est l'ensemble des {f(y), y dans B}.
Mais euh sinon je vois pas pourquoi passer autant de temps dessus, c'est totalement intuitif : tu sais que comme A se trouve dans B, bah avec B, par f tu atteindras tout ce que tu as pu atteindre dans A...
Jean-Luc97233,
ton dessin est faux et c'est ça qui te perturbe. Si tu fais de f(B) un ensemble totalement disjoint de f(A), tu utilises comme hypothèse le contraire de ce que tu veux démonter. le mieux est de ne pas représenter f(B) ou seulement en pointillés, et, à priori, avec une partie commune avec f(A) (deux sous-ensembles ont une intersection, éventuellement vide). Ensuite, pour ta compréhension, sur le dessin, tu prends un élément qui est dans f(B) mais pas dans f(A) et tu regardes ses antécédents. Puis tu prends un élément qui est à la fois dans f(A) et f(B), et tu regardes où sont ses antécédents (il y en a un dans A, car ... donc il est dans B).
Ensuite, il faut rédiger une preuve, qui doit utiliser les définitions et les transformer par application des règles en ta conclusion. Ce n'est pas une question d'écriture symbolique, mais d'application des règles. C'est ce que tu as fait en 4 lignes. Le passage de la ligne 2 à la ligne 3 est l'application de la définition de f(B). Tout simplement.
Cordialement.
Bonjour,
Quelle question surprenante !J'ai repris la totalité de ta démonstration :
1)Supposons
2)on a
3)donc
4)donc
Si je n'ai rien oublié, en quoi l'égalité de la ligne 2) permet de déduire que x appartient à f(B) à la ligne suivante ?
En ligne 1) il y a la définition de l'image directe de
... Puis en ligne 2) c'est exactement la même écriture de cette définition, ... mais pour
Cdt
Dernière modification par PlaneteF ; 17/05/2015 à 11h49.
Ça dépend du type de démonstration utilisé il me semble. Il y a des démonstrations qui n'utilisent que des arguments en français. ^^
Je pense que ce qui compte dans une démonstration c'est qu'on visualise bien pourquoi la propriété est vraie, et qu'on ne fasse pas simplement confiance à des étapes intermédiaires sans visualiser le tout. =)
Si la démonstration est en français, elle applique, en français, des règles. Ce n'est pas une question de conviction, on n'est pas au tribunal.
Le message #5 est bien une preuve écrite en français.
Et une preuve peut être tout à fait correcte sans qu'on comprenne pourquoi la propriété est vraie les preuves sur l'infini, le théorème de Tarski, ...). La preuve mathématique ne convainc pas, elle force à accepter le résultat. Si on accepte l'hypothèse et les règles des maths, la conclusion est assurée. Qu'on comprenne ou pas.
Cordialement.
Oui, mais il n'y a pas forcément de transformation.
Oui oui tout à fait nous sommes d'accord, ça n'est pas ce dont je parle. Je ne parle pas de la correction de la preuve.
On parle de preuve donc il va de soi que tout ce qu'on fait doit être rigoureux. Ce qui est parfaitement compatible avec la compréhension profonde du "pourquoi c'est vrai", de la visualisation. Pour moi c'est toujours possible de visualiser tout ce qu'on fait, c'est extrêmement difficile dans certains cas mais jamais impossible il me semble.
Bah si ce qu'on veut est simplement savoir si un théorème est vrai ou faux sans rien capter, oui ça marche.
Je ne pense pas que ça soit très intéressant de faire des maths simplement pour vérifier des propriétés comme un ordinateur.
Moi ce qui m'intéresse c'est de comprendre des trucs, pas que je constate "ah bah c'est vrai, les calculs le disent".
En plus, les calculs, bonjour les erreurs, si on ne capte rien on est comme un chirurgien aveugle, on manipule des outils avec des règles de logique mais une erreur de signe et paf tout s'écroule sans qu'on n'ait aucun moyen de s'en apercevoir.
Il me semble qu'en visualisant, à rigueur égale, on n'a beaucoup moins de chance de se planter puisqu'on comprend tout ce qu'on fait en permanence, ça prend juste beaucoup plus de temps, mais c'est un choix.
Les exemples que j'ai en tête sont des exemples de géométrie, d'algèbre ou de topologie, il y a vraiment souvent des arguments extrêmement visuels qui sont beaucoup plus riches et profonds qu'une preuve par calculs sans visualisation.
Après peut-être que je ne connais pas assez de maths pour avoir pu rencontrer de cas où ça ne marchait pas du tout, ça serait dommage, mais bon...
Effectivement,
tu manques encore de Background en maths. Pour l'instant tu as seulement effleuré les bases des maths. Et l'idée de "tout comprendre" prend des sens de plus en plus variés au fur et à mesure qu'on étudie. On en vient à saisir que ce qu'on appelle "comprendre" peut relever plus de l'habitude que d'une pensée profonde. Et on s'aperçoit (surtout en enseignant ou expliquant) qu'on n'avait pas vraiment compris ce qu'on a fait au lycée ou en L1.
Tu parles de topologie : En métrique, on peut encore se guider sur l'intuition géométrique (et encore, si la métrique n'est pas trop tordue). En topologie générale, ça devient délicat !
Mais évidemment, comprendre la démarche générale est toujours nécessaire. Sinon on a du mal à saisir la justesse de la preuve. D'ailleurs, j'avais proposé à Jean-Luc de corriger son dessin et de raisonner dessus. Mais cela paermet de bien saisir ce qu'on va écrire dans la preuve. La preuve elle-même ne parle pas de compréhension, mais d'application de règles.
Cordialement.
Bonjour,
Vous visualisez les morceaux d'une sphère qui permettent de construire 2 sphères identiques ? Si vous pouviez nous faire un petit schéma vite fait ...
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse
Mais visualiser, à mon sens, est bien plus large que "faire un schéma dans sa tête" ou raisonner avec des objets en 2D ou 3D. Je dois m'être mal exprimé.
C'est visualiser par opposition à "comprendre ligne à ligne et appliquer des théorèmes en perdant le sens de ce qu'on fabrique". C'est un type de compréhension.
Pour ça que la question de Médiat, je ne sais déjà pas y répondre car je ne connais pas de démonstration de Banach-Tarski mais en plus parce que si ça se trouve (je ne sais pas) la visualisation, si elle existe, sera de nature assez différente d'un schéma au crayon à papier.
Mais si on comprend le sens de la démonstration en un bloc en ayant une "visualisation", en comprenant très profondément pourquoi c'est vrai, là ça m'intéresse.
Autrement je ne sais pas trop à quoi ça rime :/
C'est peut-être ce que voulait dire
Si pour vous visualiser veut dire "comprendre le théorème et sa démonstration" que vous préférez par opposition à "comprendre une à une chaque ligne de la démonstration sans vision globale", vous n'allez pas trouver beaucoup de contradicteurs ; c'est d'ailleurs un reproche que l'on pourrait faire à beaucoup de mathématiciens amateurs qui rédigent leurs travaux sans les introduire mais en commençant par des calculs que personnes n'a envie de suivre sans savoir où on va ni pourquoi on y va.
PS : Pour Banach-Tarski, ne cherchez pas, cela nécessite des volumes de mesure nulle
Dernière modification par Médiat ; 17/05/2015 à 19h32.
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse
Bah c'est pour ça que je disais "visualiser" parce que c'est pas complètement comprendre dans ce que je pense.
Bon je vais prendre un exemple concret : en géométrie, dans mes cours, on fait souvent "voici le problème géométrique (par exemple trouver l'enveloppe d'une famille de droites définie géométriquement), on le traduit en équations, on résout les équations, on simplifie le résultat trouvé, hop : "c'est l'équation d'une cardioïde" (par exemple) ".
Bon, on a strictement tout compris comment faire, mais on n'a absolument pas compris pourquoi la famille de droite dessinait une cardioïde, c'est juste qu'on sait que c'est le cas par le calcul.
Alors que si on passe par de la géométrie pure (uniquement avec des formes et des angles) et qu'on regarde qu'est-ce qui se passe, là on observe pourquoi c'est effectivement une cardioïde.
Vous me direz "bon c'est de la géométrie c'est visuel" mais ce genre de truc arrive aussi en algèbre en voyant les matrices sous un certain angle ou en voyant la transformation comme ci ou comme ça.
C'est un point de vue duquel le théorème est évident en fait, "ça se voit".
Bon ça n'est pas du tout faisable d'être "évident" à chaque fois, mais c'est faisable d'augmenter le niveau d'évidence à son maximum.
De trouver une sorte de point de vue "canonique" au problème.
Mon schéma est volontairement faux. C'était un contre exemple pour montrer qu'il ne semblait pas contradictoire avec la démonstration.
Effectivement , comme vous me l'avait fait remarquer PlaneteF et gg0, j'ai complètement oublié qu'il ne s'agissait en fait que de la définition...l'art et la manière de passer à côté de l'évidence.
Merci pour tout et a tous.
Cordialement
Je vois que dans la foulée de ma petite question j'ai soulevé un débat tout à fait fascinant
