Densité, somme de variables aléatoires, loi uniforme

[Binomes]

Bonjour,

Dans un exercice que j'essaye de résoudre, on considère X et Y, deux variables aléatoires indépendantes suivant une loi uniforme sur [0,1]
----
Une densité de X et Y peut donc être donnée par:

f(x)=1 sur
f(x)=0 sinon
----
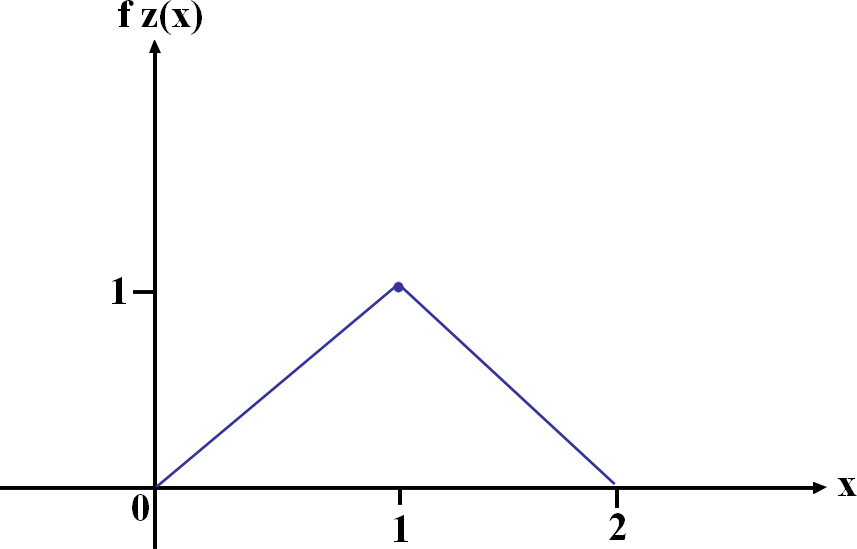
Soit Z= X + Y, dont on veux déterminer une densité.
----
A l'aide du produit de convolution, je pose:



Donc:
-Si


-Sinon


Est-ce exact ?
Je pose la question car j'ai notamment du mal à comprendre comment les bornes de l'intégrale sont définies lors d'un produit de convolution.

Merci d'avance pour vos réponses !
-----

[minushabens]

Tu trouves que Z suit la loi uniforme sur [0,1]. Comment est-ce que ça pourrait être exact? C'est facile de voir que, puisque P(X>0.5)=P(Y>0.5)=1/2 alors P(Z>1)>=1/4

[gg0]

Désolé Binomes, mais c'est faux.

Une bonne idée serait de regarder comment sont représentées les fonctions f(t) et f(x-t). La première est fixe. La deuxième dépend de la valeur de x. Tu pourras en déduire la représentation de f(t)f(x-t) suivant les valeurs de x.
Ensuite, si une fonction h est nulle sur et avec a<b, alors il est facile de comprendre que


Bon travail !

NB : Si X prend des valeurs entre 0 et 1, Y prend des valeurs entre 0 et 1, alors X+Y prend des valeurs entre ...

[Binomes]

Merci pour vos réponses !

Logiquement,



Je prends ensuite en considération (x-t):



J'en déduis:



Le problème c'est que je retombe sur la même valeur, qui est fausse.
A partir de quelle étape est-ce que je commet une erreur ?

[A voir en vidéo sur Futura]

[gg0]

Tu intègres de 0 à 1. Donc il faut aussi que tu en tiennes compte. Au passage, dans la dernière ligne de calcul, tes bornes de l'intégrale sont inversées. C'est cette intégrale (même avec les bornes dans le bon sens) qui est fausse. Tu n'as pas représenté f(x-t), tant pis pour toi !

NB : Tu raisonnes à l'envers, ce n'est pas t qu'il faut déterminer en fonction de x, t varie de 0 à 1, c'est l'intégrale qu'il faut calculer suivant les valeurs de x ...

[Binomes]

A l'aide de tes conseils, voici ce que j'effectue:

donc

Et je découpe en cas:

- Cas où x>1 ou x<-1 (<=> x+1<0):



-Cas où



Si ce n'est pas correct, serait-il possible d'avoir un exemple ?
Parce que je suis vraiment perdue et que chaque exemple que je trouve me rend un peu plus confuse ...

[gg0]

Tu ne suis pas mes conseils, faut-il que je continue ?

Allez, un dernier effort de ma part : Représente f(x-t) pour x=-0,5, x=0,5, x=1, x=1,5, x=2,5.

[Binomes]

Je suis désolée si je te donne l'impression de ne pas suivre tes conseils, c'est juste que mon niveau étant ce qu'il est, j'ai du mal à les comprendre >.<

Je récapitule un peu ce que je sais:

Comme X et Y suivent la loi uniforme sur [0,1], leur densité est:

- si
- sinon

Lorsque tu me conseille de représenter f(x-t), j'aurais donc tendance à penser que:

- si
- sinon

En prenant x=1, j'aurais tendance à déduire que:

- si ce qui correspondrait au cas où
- sinon

Pour x=0,5:

- si ce qui correspondrait au cas où
- sinon

Pour x=-0,5:

- si ce qui correspondrait au cas où
- sinon

Pour x=1,5:

- si ce qui correspondrait au cas où
- sinon

Pour x=2,5:

- si ce qui correspondrait au cas où
- sinon

Si ce n'est pas là ce que tu entend par réprésenter f(x-t) en fonction de x, je m'excuse et te remercie pour la patience dont tu as fais preuve

[minushabens]

Il faut utiliser la fonction indicatrice 1_[0,1] et intégrer de -infini à +infini.

[gg0]

Moi, je te proposais de "représenter" une fonction. Tu fais ça depuis la seconde, c'est assez facile ici, et tu as déjà fait l'essentiel. Fais des dessins au brouillon, et regarde ce que donne f(t)f(x-t) dans différents cas.

[Binomes]

J'ai tout recommencé depuis le début et ai passé pas mal de temps à cogiter tout ça.
J'ai notamment dessiné les intervalles de f(t) (0 à 1) et f(x-t) (x-1 à x) les unes par rapports aux autres dans les différents cas.

Voilà mon raisonnement actuel:
Posons d'abord,



Si , , 0 sinon.

Si , soit alors , 0 sinon.

On observe plusieurs cas:

- x<0,

- x-1>1 <=> x>2,

-,

-,

Et le schéma correspondant:


Il y a une erreur dans ce schéma, l'axe des abcisses devrait correspondre à fz(x)

Est-ce correct ?

[gg0]

Les résultats sont bons, j'attends de voir la pièce jointe ... je n'ai pas compris le calcul dans le cas 1<x<2 (la borne 2) : la fonction ent nulle en dehors de [x-1,1].

[Binomes]

Cette borne correspond effectivement au cas [x-1,1], je me suis trompée en la réécrivant, j'ai dû m'inspirer de l'équation au lieu de correctement le recopier.

Mais merci beaucoup à vous !
J'avais énormement de mal à comprendre comment fonctionnait les produits de convolution, je pense m'en sortir un peu mieux maintenant

[gg0]

Il y a une erreur dans ce schéma, l'axe des abcisses devrait correspondre à fz(x)

Non, non, c'est bien x pour les abscisses et fz(x) pour l'axe des ordonnées

[Binomes]

Oui, j'avais modifié l'image en fin de compte mais oublié de supprimer cette phrase