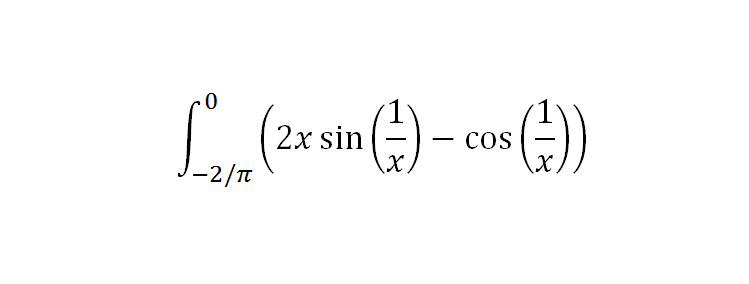touver la nature de cet integrale
Discussions similaires
-
Par invite9d7acbe1 dans le forum Mathématiques du supérieur
Réponses: 12
Dernier message: 24/06/2014, 13h07
-
Par invite5803d5d8 dans le forum Mathématiques du supérieur
Réponses: 1
Dernier message: 21/10/2009, 21h06
-
Par invite9f7f0e56 dans le forum Mathématiques du supérieur
Réponses: 1
Dernier message: 22/01/2009, 22h52
-
Par invite616e6f6a dans le forum Mathématiques du supérieur
Réponses: 7
Dernier message: 18/09/2008, 17h21
-
Par inviteae6e334f dans le forum Mathématiques du supérieur
Réponses: 2
Dernier message: 04/11/2007, 19h22