Bonjour, voici, pour m'entrainer, ce que je trouve sur Wikiversity :
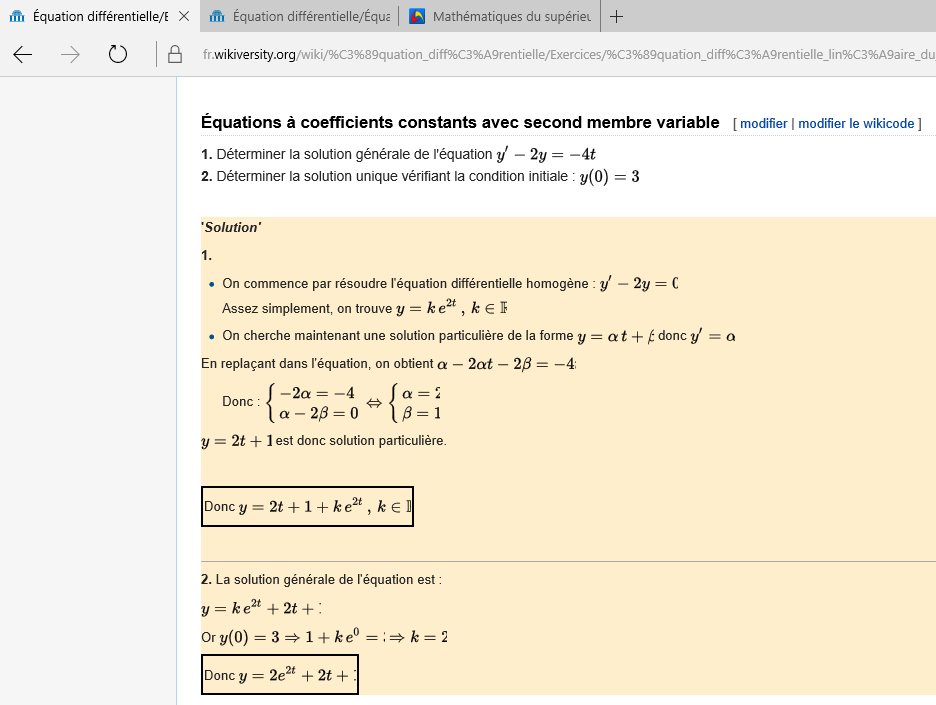
Je ne comprends pas dans la solution 1 comment on passe de : a - 2at - 2b = - 4t à : - 2a = - 4 et : a - 2b = 0
Je dois apprendre les équations différentielles du 1er ordre de toutes sortes pour la rentrée, merci si vous pouvez m'éclairer.
Le point clé, c'est que a-2at-2b = -4t pour toutes les valeurs de t. Si on note P(t) = (4-2a)t + (a-2b) , on a donc P(t) = 0 pour tout t. Donc P est le polynôme nul, donc ses coefficients sont nuls, d'où le résultat.
P(t) = (4-2a)t + (a-2b) = 0
Ok j'ai compris, on met tout d'un coté du "=" et les 2 calculs en parenthese n'ontpas d'autres choix que de donner 0 pour tout "t" ok ok merci, j'ai compris maintenant.
Aussi je trouve ceci, ça me bloque depuis 2 bonnes heures :
Sur les 3eme et 4eme lignes, on a y = k.exp^(-ln(1+x^2)) et plus bas y = k/(1+x^2)
Ca voudrait dire que : A.exp^(-Ln(B)) = A/B ?? Je vous le demande, comment on en arrive là ?
Simplement en utilisant ces deux propriétés de base :
-ln(x) = ln(1/x)
exp(ln(y)) = y
Dac merci, mais par contre pour la suite, je suis complètement largué. La méthode de variation de la constante, j'y comprends vraiment plus rien. Vous n'auriez pas un cours à la manière douce ?
Bonjour.
la méthode de la variation de la constante, c'est simplement ce qui est fait : Pour l'équation sans second membre, on a trouvé une solution qui dépend d'une constante (ici k). On cherche une solution de l'équation complète en prenant la même expression, mais où la constante k est remplacée par une fonction de x (donc varie, d'où le nom de la méthode). Tu verras en faisant les calculs pourquoi c'est intéressant (on trouve une équation différentielle élémentaire k'(x)= ...).
Après, la difficulté des équations différentielles est très souvent, pour les débutants, la connaissance des règles de base des calculs et des fonctions de base (voir comme exemple la réponse de Tryss2, qui donne des formules très élémentaires). Donc connaître correctement les fonctions utilisées et les calculs basiques est une priorité. C'est d'ailleurs la seule manière douce !
Cordialement.
Mais pouvez vous m'expliquer, sur la ligne qui commence par (E1), comment en se retrouve avec k'=1+3x svp.
J'ai remarqué que les deux grosses fractions centrales s'annulent, mais donc k' serait égal à ((1+3x2)*(1+x2))/(1+x)
j'arrive pas à simplifier ça à 1+3x... Ah moins que c'est tout bête ?
Il manque des bouts qui sont coupés par la mise en page !
Il faut lire à la ligne (E1)
Donc on a directement que, d'où, k(x) = C + x+x^3
A noter : faire soi-même les calculs plutôt que de les lire permet de bien les comprendre.
gg0 oui évidemment, c'est exactement ce que j'essay de faire, puis ensuite je verifie leur correction, cependant sur wikiversity j'ai pas l'impression que tout est clair, par exemple (je solicite encore votre aide haha) :
Sur la ligne qui commence par (E2), quand ils font la primitive de k', pour arriver à k, ça ne peut pas être bon ! En effet quand je dérive k, j'obtiens 1/(2+2x^2), pas vrai ? Mais j'ai l'impression que vous allez me dire pourquoi, je ne suis pas super doué en ce qui concerne trouver des primitives de fonction avec plusieurs variable qui se balladent...
Et pour l'équation E3, comment passent ils de y = ke^(-ln(x^2-1)/2) à y = k/Racine(x^2-1) ?? La j'ai tenté les deux calculs avec une valeur de x au pif, mais je ne trouve pas le même résultat, mais c'est sensé être égal ? J'attend impatiamment vos réponses, confirmez moi que je ne suis pas fou svp merci
Ah non pour E2 je dis vraiment n'importe quoi, c'est bien ça, j'avais oublié comment on dérive les ln... Je suis vraiment un bleu haha.
Mais si vous pouvez m'expliquer au moins pour l'équation E3 svp merci beaucoup (et désolé du double post, j'ai essayé de modifier, mais c'est compliqué, il faut demander l'autorisation aux modérateurs, ils dorment pas à cette heure ci ?).
C'est bon j'ai ma réponse, désolé d'avoir perturbé le forum maths sup, en fait j'ai découvert sur le net que u*ln(x) = ln(x^u) (..d'ailleur c'est vraiment ça ?)
Et en effet j'avais fait un calcul qui ne donnait pas la même chose, normal je suis bête, j'ai du mettre la constante à 1 pour essayer, mais ça ne peut justement pas marcher, c'est elle qu'on recherche ! Donc pour que ça donne le même résultat, on doit placer la bonne constante.. Voilà désolé bonne nuit tout le monde !
Bonjour.
" si vous pouvez m'expliquer au moins pour l'équation E3" Il faudrait avoir un document sérieux ! Ici, il n'y a rien dans l'équation après =. La suite laisse penser que c'était =x.
je ne sais pas trop ce qu'il faut expliquer, vu que c'est ce qui est fait !!!
"j'avais oublié comment on dérive les ln", "j'ai découvert sur le net que u*ln(x) = ln(x^u)" : A quoi sert de traiter des équations différentielles si tu ne connais pas les règles de calcul sur les fonctions de base ? Fais ce travail, revois les cours de lycée (fonctions élémentaires, trigo, ln et exp, dérivées, primitives élémentaires), et après tu pourras faire ce travail. Tu ne te présenterais pas à un triathlon sans savoir nager ...
Cordialement.
Oui oui effectivement tu n'as pas tort je vais suivre tes conseils pour ce soir, j'en ai oublié un bon paquet c'est certain. C'est ça qui me bloque !
