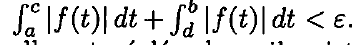Fonction intégrable

[kizakoo]

Bonjour, je cherche à démontrer le résultat suivant:
si f est intégrable sur un intervalle de bornes a et b (dans R barre) alors il existe un segment [c,d] tel que :




j'ai essayé d'utilisé la convergence des deux fonctions (vers la même limite l) : g(x)= quand x tend vers b et h(x)= quand x tend vers a :

- Par définition on a l'existence, d'un A tel que pour tout x inférieur à A:



de même on a l'existence d'un B tel que pour tout x supérieur à B :



Je peux prendre le b dans ]a,A] et c dans [B,b[ .... mais je ne parviens pas à l'inégalité demandée.

Je vous remercie énormément de votre aide .
-----

[gg0]

Bonjour.

Intuitivement, j'aurais procédé autrement : supposé l'intégrabilité sur [a,b], puis en niant la propriété (tu as oublié le "quel que soit .."), prouvé qu'il y a contradiction.
Donc en supposant qu'il existe un tel que quels que soient c et d tels que on a

j'aurais comparé, pour c et d tendant respectivement vers a et b les intégrales
et

Pour ce que tu as fait, je n'ai pas d'idée.

Cordialement.

[kizakoo]

Oui tout à fait je suis parvenu au résultat . Je n'ai pas pensé à la comparaison et ai introduit le l qui crée des problèmes ....

Merci gg0

P.S: on met plutôt "norme de f" dans l'inégalité car epsilon strictement positive et on ignore le signe de l'intégrale (?)

[gg0]

Effectivement, j'ai tapé un peu vite

[A voir en vidéo sur Futura]