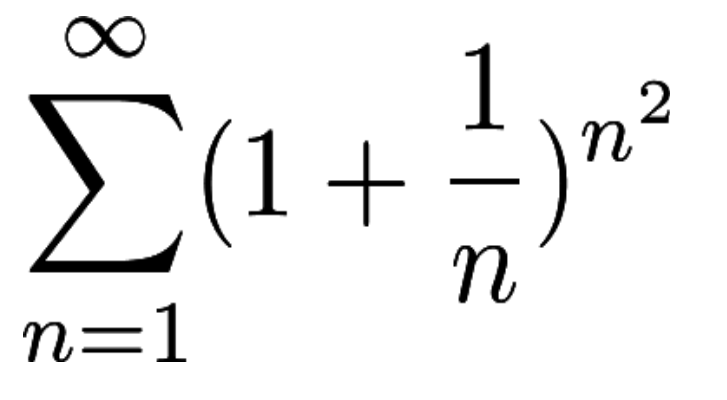Convergence d'une série particulière

[MrSteveWonder]

Bonjour !
Je suis à la recherche d'aide pour évaluer la convergence d'une série qui me pose problème . Sans me donner directement la réponse , j'aurais besoin d'aide pour trouver au moins une piste , car j'ai essayé quelques critères sans succès...
La dite série est la suivante :


J'avais penser au critère de Cauchy puisque le terme en entier est une puissance de n , mais il s'agit de n carré en exposant et je ne peux pas vraiment l'appliquer 2 fois simultanément ...
d'Alembert aussi semble peu fructueux et le test de divergence me fait apparaître une indétermination 1 exposant infini...

Merci de votre aide !
-----

[ansset]

c'est sacrément divergent , de plusieurs manières
par exemple ( pour n>1 ) :
(1+1/n)^n² > 1+n²/n = 1+n, donc les termes de la suite divergent déjà, ne parlons donc même pas de la somme.