Point intérieur

**mehdi_128** · 19/09/2018, 14h25

Bonjour,

Voici un résultat que je trouve évident mais je n'ai pas compris la démonstration de l'auteur

Dans $\text{[math]}$ , si $\text{[math]}$ avec $\text{[math]}$ alors tout point de l'intervalle ouvert $\text{[math]}$ est un point intérieur de I.
Je trouve cela évident car c'est équivalent à dire que : $\text{[math]}$ , I est un voisinage de x. On peut toujours inclure une boule ouverte de centre x et de rayon $\text{[math]}$ dans $\text{[math]}$ .

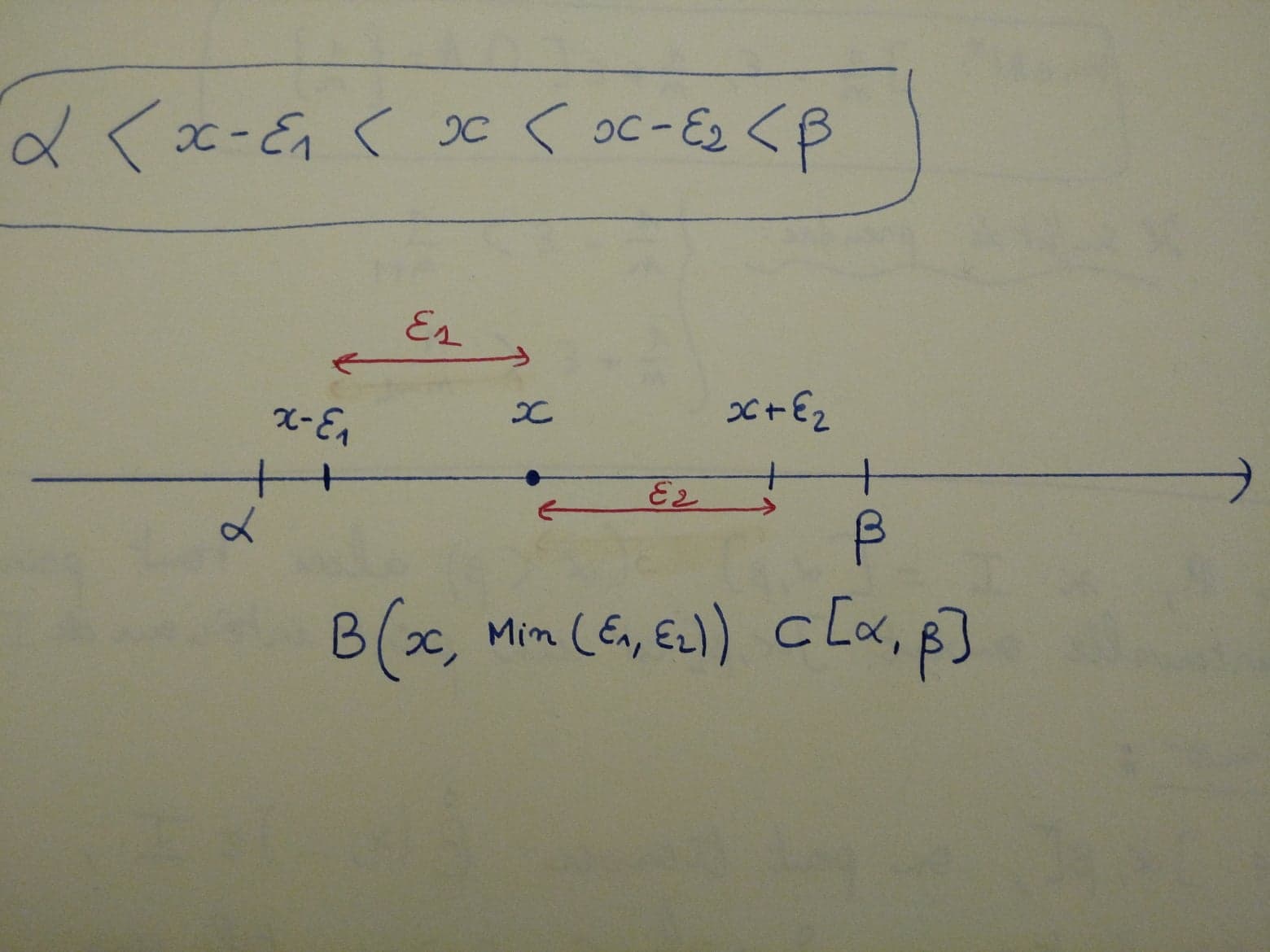
Démonstration :
Si $\text{[math]}$ alors on peut trouver une boule ouverte de centre x contenue dans $\text{[math]}$ , il suffit de trouver 2 réelles $\text{[math]}$ tels que : $\text{[math]}$ puis poser $\text{[math]}$

J'ai rien compris à la démonstration

**minushabens** · 19/09/2018, 14h45

Il ne dit pas comment trouver epsilon1 et epsilon2. Mais il est clair que l'intervalle ]x-epsilon,x+epsilon[ est la boule ouverte cherchée.

edit: non, il y a bien une erreur dans la démonstration. Il faut trouver eps1 et eps2 tels que alpha < x-eps1 < x < x+eps2 < beta

**Anonyme007** · 19/09/2018, 14h59

Bonjour,

Soit $\text{[math]}$ :

Alors, on peut remarquer que : $\text{[math]}$ , non ?

On prend, donc : $\text{[math]}$ , et on a ainsi :

$\text{[math]}$

D'où : $\text{[math]}$ .

Cordialement.

Edit : Grillé.

**mehdi_128** · 19/09/2018, 15h02

Envoyé par minushabens

Il ne dit pas comment trouver epsilon1 et epsilon2. Mais il est clair que l'intervalle ]x-epsilon,x+epsilon[ est la boule ouverte cherchée.

edit: non, il y a bien une erreur dans la démonstration. Il faut trouver eps1 et eps2 tels que alpha < x-eps1 < x < x+eps2 < beta

Bien vu ça marche mieux

J'ai fait un dessin, par contre je me demande : pourquoi on doit prendre le Min ? Ce point m'échappe.

Nom : 41968174_2286108834750705_3289279855870345216_n.jpg
Affichages : 592
Taille : 78,3 Ko

Nom : 41968174_2286108834750705_3289279855870345216_n.jpg
Affichages : 592
Taille : 78,3 Ko

A voir en vidéo sur Futura · Aujourd'hui

**Amanuensis** · 19/09/2018, 15h05

Edit: doublon partiel avec#3

Ou (autre correction)

poser $\text{[math]}$ (et alors vaut mieux les appeler autrement...)

L'avantage est que l'existence d'intermédiaires vient directement de l'ordre dense. Et tant qu'à faire, on peut prendre (x+α)/2 et (x+β)/2, on peut être directement constructif et s'appuyer sur l'arithmétique!

pourquoi on doit prendre le Min ? Ce point m'échappe.

Pour que la boule de rayon ε et de centre x soit incluse dans l'intervalle, sans que «ça déborde» d'un côté ou de l'autre.

**Anonyme007** · 19/09/2018, 15h09

En fait, il n'y'a pas que ce choix de sous intervalle : $\text{[math]}$ , de centre : $\text{[math]}$ , avec : $\text{[math]}$ .
On peut faire par exemple un autre choix, par exemple : $\text{[math]}$ avec : $\text{[math]}$ de votre choix.
On peut choisir un autre avec : $\text{[math]}$
ou bien : $\text{[math]}$ ...
Il y'a une infinité de choix possible pour ce sous intervalle de centre $\text{[math]}$ : $\text{[math]}$ .
Tu es libre de choisir celui qui te plaît.

**mehdi_128** · 19/09/2018, 15h10

Envoyé par Anonyme007

Bonjour,

Soit $\text{[math]}$ :

Alors, on peut remarquer que : $\text{[math]}$ , non ?

On prend, donc : $\text{[math]}$ , et on a ainsi :

$\text{[math]}$

D'où : $\text{[math]}$ .

Cordialement.

Edit : Grillé.

J'ai rien compris et ça sort d'où ces valeurs absolues ?

**Anonyme007** · 19/09/2018, 15h27

Envoyé par mehdi_128

Bien vu ça marche mieux

J'ai fait un dessin, par contre je me demande : pourquoi on doit prendre le Min ? Ce point m'échappe.

Pièce jointe 373638

Pour l'adapter à la définition d'une boule $\text{[math]}$ .

Le centre $\text{[math]}$ d'une boule $\text{[math]}$ doit être à meme distance de ses deux bornes $\text{[math]}$ et $\text{[math]}$ .

Si on s’arrête simplement à l'intervalle : $\text{[math]}$ avec : $\text{[math]}$ , la distance $\text{[math]}$ est différente de la distance $\text{[math]}$ .

Il faut donc les égaliser en unifiant le choix des bornes, et ce en choisissant le minimum des deux : $\text{[math]}$ et $\text{[math]}$ .

**mehdi_128** · 19/09/2018, 15h32

Envoyé par Amanuensis

Edit: doublon partiel avec#3

Ou (autre correction)

poser $\text{[math]}$ (et alors vaut mieux les appeler autrement...)

L'avantage est que l'existence d'intermédiaires vient directement de l'ordre dense. Et tant qu'à faire, on peut prendre (x+α)/2 et (x+β)/2, on peut être directement constructif et s'appuyer sur l'arithmétique!

Pour que la boule de rayon ε et de centre x soit incluse dans l'intervalle, sans que «ça déborde» d'un côté ou de l'autre.

J'ai pas compris votre Min

Je suis en train d'étudier le niveau L1 et sans prof donc je pense pas avoir le niveau pour comprendre votre intervention.

Mais pour le $\text{[math]}$ j'ai compris en faisant un exemple.

J'essaie de le démontrer :

On a dit que : $\text{[math]}$

Posons : $\text{[math]}$
Soit x un élément de $\text{[math]}$

1er cas
Si $\text{[math]}$ alors $\text{[math]}$

$\text{[math]}$

2ème cas
Si $\text{[math]}$ alors $\text{[math]}$

$\text{[math]}$
Mais $\text{[math]}$

Donc comme : $\text{[math]}$ on a : $\text{[math]}$

Ainsi : $\text{[math]}$

Le résultat est démontré

**Anonyme007** · 19/09/2018, 15h34

Envoyé par mehdi_128

J'ai rien compris et ça sort d'où ces valeurs absolues ?

Les valeurs absolues sont présentes ici pour éviter que : $\text{[math]}$ et $\text{[math]}$ soient négatives, sinon, on aura dans certains cas : $\text{[math]}$
Alors, on ajoute les valeurs absolues pour s'assurer qu'on aura effectivement une inclusion : $\text{[math]}$ .

**mehdi_128** · 19/09/2018, 15h43

Envoyé par Anonyme007

Pour l'adapter à la définition d'une boule $\text{[math]}$ .

Le centre $\text{[math]}$ d'une boule $\text{[math]}$ doit être à meme distance de ses deux bornes $\text{[math]}$ et $\text{[math]}$ .

Si on s’arrête simplement à l'intervalle : $\text{[math]}$ avec : $\text{[math]}$ , la distance $\text{[math]}$ est différente de la distance $\text{[math]}$ .

Il faut donc les égaliser en unifiant le choix des bornes, et ce en choisissant le minimum des deux : $\text{[math]}$ et $\text{[math]}$ .

Ah j'ai compris ce que vous avez fait : vous avez explicité epsilon1 et epsilon2 comme le centre respectif des intervalles entre alpha et x et x et beta ! Comme ça ça vous donne le rayon de la boule centrée en x.

Mais démontrer votre résultat revient au même que la démo que j'ai faite je pense

Vous pensez quoi de ma démo ?

**gg0** · 19/09/2018, 15h48

Mehdi_128, laisse tomber les affirmations de Anonyme007, elles sont fausses (essaie avec $\text{[math]}$ .

Cordialement.

Pablo, ça ne sert à rien de vouloir aider les autres si tu ne vérifies pas soigneusement tes affirmations. Et ici, c'est pire, tu détournes Mehdi d'une bonne solution, tu lui fais perdre son temps.

**Anonyme007** · 19/09/2018, 15h59

Je corrige :

On a :

$\text{[math]}$

au lieu de :

$\text{[math]}$

**gg0** · 19/09/2018, 16h05

C'est pas mieux !

Arrête d'inventer !! Tu aurais au moins pu vérifier avec les valeurs que je propose, tu aurais évité le ridicule !!
Tu passes ton temps à parler de conjectures de haut niveau mais tu ne sais pas faire des maths de première scientifique, ne perturbe pas les autres.

**Anonyme007** · 19/09/2018, 16h15

Je corrige :

On a :
$\text{[math]}$

au lieu de :

$\text{[math]}$

J'espère que ça marche.

**gg0** · 19/09/2018, 16h33

Toujours pas

Bon, tu arrêtes de faire l'idiot ??? D'autant que Mehdi a déjà plusieurs solutions et qu'il n'a pas de temps à perdre à vérifier tes âneries.

**Anonyme007** · 19/09/2018, 16h36

**ansset** · 19/09/2018, 16h38

mais que viennent faire les valeurs absolues dans cet exercice ?

**Anonyme007** · 19/09/2018, 16h42

@ansset :
J'ai eu du mal à exprimer formellement : la moitié de la distance qui sépare $\text{[math]}$ de $\text{[math]}$ et $\text{[math]}$ . Alors, ça a besoin d'utiliser les valeurs absolues.

**gg0** · 19/09/2018, 16h47

Niveau première S. Pablo ne pense pas, ne sait pas, écrit au petit bonheur en espérant de "tomber juste". Ça fait des années qu'il fait ça en croyant qu'il fait des maths ...

Salut Ansset.

**ansset** · 19/09/2018, 17h03

Salut aussi, mais le fil a été initié par Medhi.
la démo est assez simple sans rentrer dans des trucs compliqués.
Cdt

**mehdi_128** · 19/09/2018, 17h29

Envoyé par ansset

Salut aussi, mais le fil a été initié par Medhi.
la démo est assez simple sans rentrer dans des trucs compliqués.
Cdt

Salut ansset

Dès lors que minushabens que je remercie a corrigé l'erreur de mon livre, j'ai mieux compris et j'ai démontré que $\text{[math]}$ est le rayon de la boule ouverte incluse dans l'intervalle I voir mon post 9. Sans utiliser de valeur absolue !

**Anonyme007** · 19/09/2018, 17h45

Relis bien ce qui est écrit dans ton cours :

Envoyé par mehdi_128

Démonstration :
Si $\text{[math]}$ alors on peut trouver une boule ouverte de centre x contenue dans $\text{[math]}$ , il suffit de trouver 2 réelles $\text{[math]}$ tels que : $\text{[math]}$ puis poser $\text{[math]}$

Il faut trouver $\text{[math]}$ et $\text{[math]}$ ... Tu ne les as pas trouver. Je te les ai trouvé à ta place, mais tu les refuse. Tant pis pour toi !

**mehdi_128** · 19/09/2018, 18h59

Non pas besoin de les expliciter je pense.

**minushabens** · 19/09/2018, 19h19

On pourrait aussi dire que ]alpha,beta[ est une boule ouverte donc un ouvert par définition, et donc un voisinage de chacun de ses points (un voisinage de x contient un ouvert qui contient x, rien ne dit que ça doit être une boule ouverte et encore moins que x doit en être le centre).

**Anonyme007** · 19/09/2018, 19h22

Tu verras dans les prochaines années si tu suis un cours d'algèbre commutative, il n'y'a que des questions de ce genre là, c'est à dire :
- Montrer qu'il existe un objet tel que :
- Montrer qu'il existe un autre objet tel que :
... etc.
.. Et montrer l'existence d'un objet, signifie en langage de la rue, trouver un tel objet concrètement ... C'est à dire le trouver appartenant à un certain ensemble. A l'examen, si tu ne précises pas quel est cet objet, tu risques de perdre quelques points. Tant pis pour toi.

**gg0** · 19/09/2018, 19h27

Anonyme007/Pablo,

il est possible que Mehdhi suive un jour un cou(rs d'algèbre commutative, mais en comprenant ce qu'il fait.
Tu es sacrément gonflé de lui donner des conseils sur béac + 4 alors que tu n'es pas capable de faire un exercice élémentaire de lycée. Tu devais avoir honte !!!

Et ce que tu racontes à la fin (montrer l'existence=trouver un tel objet concrètement) prouve bien que tu n'as rien compris au fonctionnement des maths !! Évite de dire n'importe quoi !!

Ça fait 10 ans que je vois tes messages sous des pseudos divers, tu as toujours refusé de faire des maths sérieusement, ne donne pas des conseils idiots aux autres, tu vas te faire virer encore d'un forum de plus.

**Anonyme007** · 19/09/2018, 19h45

Je suis sur plus de 6 forums, 2 d'entre eux depuis 11 ans, et je n'ai jamais été viré vu la qualité de mes réponses que tu manques d'avoir. Il n'y'a que les modérateurs qui décident de virer qui. Le bannissement est surtout adopté lorsque quelqu'un ne cesse pas de traîner sur le forum en insultant n'importe qui. et si tu comptes le nombre d'insultes sur ce fil, il y'a plus de 4 insultes : Tu m'as appelé idiot, ane ... etc, et j'ai évité de répondre similairement. C'est toi qui doit commencer à faire attention aux bannissements gg0.

**ansset** · 19/09/2018, 23h11

oups, on se calme !
la dém, comme vient de le dire Medhi lui même n'a pas besoin de complication avec les valeurs absolues.
au moins LUI l''a visiblement compris et c'est ce qui importe.
pour le reste ( les chtites querelles persos ) , ça me passe très au dessus de ma petite caboche

**mehdi_128** · 23/09/2018, 02h56

J'ai une nouvelle question sur l'intérieur d'un ensemble :

Soit A une partie d'un espace métrique : a t-on toujours $\text{[math]}$ ?

Je pense que oui mais je suis pas sûr.

Point intérieur

Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Re : Point intérieur

Discussions similaires

point intérieur-ouvert d'un point

méthode du point intérieur

Point critique à l'intérieur d'une orbite périodique

Comment savoir si un point est à l'intérieur d'une ellipse

Point de rosée en isolation intérieur sur parpaings