Bijection réciproque

**mehdi_128** · 02/10/2018, 20h14

Bonsoir,

Je suis dans la démo du théorème suivant et je pense encore avoir trouvé une coquille dans mon livre :
Soit f une fonction continue et strictement monotone sur un intervalle I. Alors sa bijection réciproque est continue sur f(I).

L'erreur que je soupçonne est le $\text{[math]}$

Selon moi faudrait prendre : $\text{[math]}$ où divisé par n'importe quel nombre positif plus grand que 1.
Sinon on aura jamais : $\text{[math]}$ et tous les raisonnement sur la croissance sont faux.

Voici la démo :

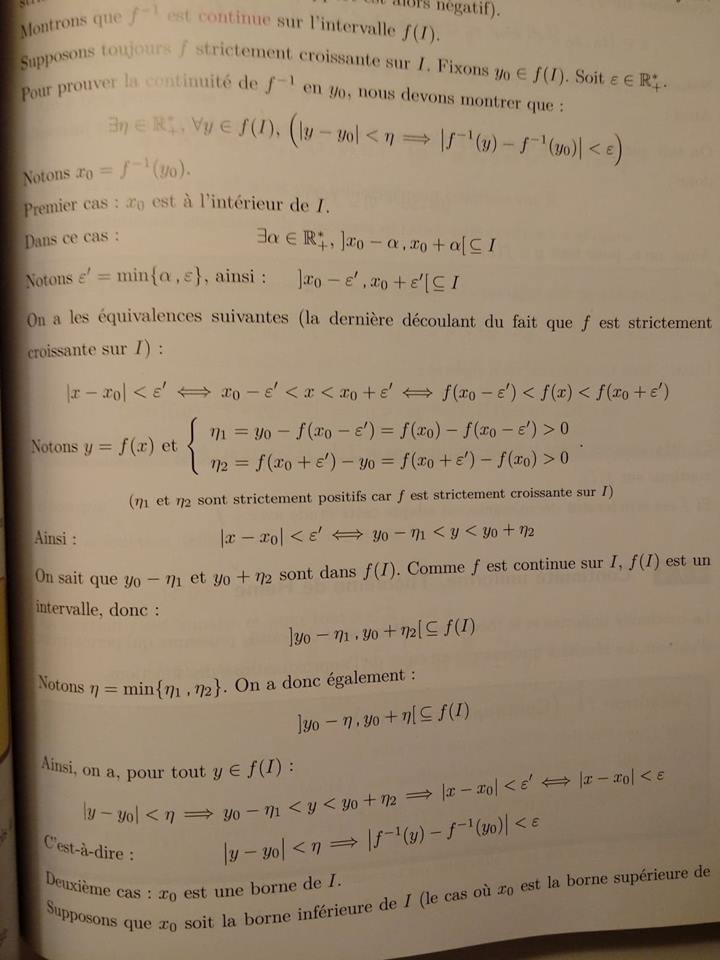
Nom : 43037209_410619012802345_3745757720347672576_n.jpg
Affichages : 642
Taille : 61,6 Ko

Nom : 43037209_410619012802345_3745757720347672576_n.jpg
Affichages : 642
Taille : 61,6 Ko

**gg0** · 02/10/2018, 22h26

Heu ... on n'a pas besoin que $\text{[math]}$ soit dans I.

**mehdi_128** · 02/10/2018, 22h55

On a pas l'ensemble de définition de f c'est bizarre. Il faudrait justifier que : $\text{[math]}$

Mais c'est le passage :

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$

Pas compris comment on peut utiliser la stricte croissante de f sur I car on sait pas si $\text{[math]}$ et $\text{[math]}$ sont des éléments de $\text{[math]}$

Et puis le $\text{[math]}$ n'a aucun intérêt alors si on prend juste le $\text{[math]}$
Vous en voyez un intérêt ?

**mehdi_128** · 02/10/2018, 23h21

Quand on utilise la stricte crissante :

Si f est strictement croissante sur $\text{[math]}$ et $\text{[math]}$ deux éléments de $\text{[math]}$ alors :

$\text{[math]}$ donne $\text{[math]}$

Dans la démo $\text{[math]}$ est inclus dans $\text{[math]}$ mais les bornes sont ouvertes !

A voir en vidéo sur Futura · Aujourd'hui

**gg0** · 03/10/2018, 09h54

1) il manque le début du texte, mais le domaine de définition de f est I (voir l'énoncé complet du théorème).
2) Il suffit de prendre au départ un $\text{[math]}$ tel que les bornes soient dans I, et il n'y a plus de problème

**gg0** · 03/10/2018, 10h02

Au lieu de chercher dans les coins des démonstrations mal écrites de ton bouquin, fais les preuves toi-même, tu gagneras du temps.
Je remarque que tu ne donnes jamais le point exact qui pose problème, comme ici, où il a fallu 3 messages pour que tu dises ce qui gêne, j'en déduis que tu te contentes de lire les preuves sans essayer de les faire toi-même. Pourquoi cette attitude d'amateur, alors que tu veux devenir un professionnel (enseignant) ? Et comme tu es flou, tu poses des questions bébêtes, comme ici cette question de domaine de définition, et tu passes pour un incompétent.
Change de méthode, fais des maths, pas de la lecture.

**mehdi_128** · 03/10/2018, 13h26

C'est impossible de trouver la preuve seul d'un théorème comme ça.

La démo est assez difficile.

Pour les démos faciles et courtes je veux bien essayer mais là c'est mission impossible.

**AncMath** · 03/10/2018, 13h35

Loin de moi l'idée de vouloir te décourager, mais il est anormal que tu trouves cette preuve difficile si tu veux enseigner. Ce théorème et sa démonstration sont triviales, si tu butes dessus, c'est qu'il y a qqch en amont que tu ne maitrise pas. A toi de localiser cette ou ces choses et de les assimiler. Quand ce sera fait, tu devrais trouver ce résultat tout ce qu'il y a de plus trivial.

invite51d17075 · 03/10/2018, 14h10

oui, je vois pas ce qui gène.
la seule coquille ( de frappe ? ) est pour moi dans l'avant dernière ligne.
$\text{[math]}$ , et non ( <=> )
mais cela ne change pas la conclusion.

ps: il est aussi certainement possible de faire plus court, mais cette démo est "détaillée".

**mehdi_128** · 03/10/2018, 14h29

Envoyé par AncMath

Loin de moi l'idée de vouloir te décourager, mais il est anormal que tu trouves cette preuve difficile si tu veux enseigner. Ce théorème et sa démonstration sont triviales, si tu butes dessus, c'est qu'il y a qqch en amont que tu ne maitrise pas. A toi de localiser cette ou ces choses et de les assimiler. Quand ce sera fait, tu devrais trouver ce résultat tout ce qu'il y a de plus trivial.

Ce n'est pas difficile en fait avec du recul mais je comprends pas que vous ne voyez pas l'erreur suivante : (il y a un un seul point qui me gêne)

SI par exemple : $\text{[math]}$
On a bien : $\text{[math]}$

Comment on peut passer à la croissance de $\text{[math]}$ en $\text{[math]}$ et $\text{[math]}$ alors que ces points n'appartiennent pas à $\text{[math]}$ (intervalle ouvert) ?
f est strictement croissante sur $\text{[math]}$ ... Pas pour des points en dehors de I !

Pour ça que je dis qu'il faut diviser le Min par 2 !

Comment on peut écrire : $\text{[math]}$ alors que $\text{[math]}$

invite51d17075 · 03/10/2018, 14h46

Comprend pas ton début , tu raisonnes à l'envers.
Dans cette partie de démo, I est un intervalle et x0 est à l'intérieur de I
I n'est pas défini par rapport à $\text{[math]}$ ni $\text{[math]}$

par ailleurs, dans cette partie de démo x0 est à l'intérieur de I
donc il existe $\text{[math]}$
puis
$\text{[math]}$ donc
$\text{[math]}$
de part la construction de $\text{[math]}$

**mehdi_128** · 03/10/2018, 14h59

@AncMaths
Voici le point incompris je l'ai localisé !

Donc quand on écrit : $\text{[math]}$

Ca veut dire que forcément : $\text{[math]}$ et $\text{[math]}$

De manière générale : si $\text{[math]}$ signifie que $\text{[math]}$ et $\text{[math]}$ ?

invite51d17075 · 03/10/2018, 15h56

avant toute rponse, il manque le début de l'énoncé.
pourquoi dis tu que I est un intervalle ouvert ?
et pour ma gouverne , j'ai oublié le sens du sigle $\text{[math]}$

invite51d17075 · 03/10/2018, 16h04

à oublier, sauf la première question.

invite51d17075 · 03/10/2018, 16h15

de fait, à la re-lecture je comprend mieux ton interrogation , mais elle a été longue à accoucher. !!!
pour éviter toute ambiguïté , il eut suffit de choisir
$\text{[math]}$

ps: car il est vrai que ton bouquin n'est pas tj très "propre".
mais ça , cela a déjà été dit.

**gg0** · 03/10/2018, 17h18

Mehdi,

je suis inquiet pour toi, car tu n'as finalement pas vu quel est le problème de ta démo, le fait que l'auteur utilise $\text{[math]}$ qui n'a aucune raison d'exister et que les incompréhensions des autres (vu que tu ne précises jamais la question) t'amènent à écrire des énormités, comme ton message #12. Même si c'est pour insister, tu ne dois pas laisser croire que tu peux penser ça !!
A ton niveau, tu ne peux pas penser que d'autres croient que " si $]a,b[ \subset I$ signifie que $a \in I$ et $b \in I$ ", tu dois connaître parfaitement la notion de "inclus".

Que de pertes de temps sur des broutilles, tu as mieux à faire que de venir ici. Par exemple essayer de rédiger une preuve sérieuse (c'est du niveau L1), ce qui te permettra de progresser.
Et arrête de croire que les maths de L1 sont difficiles, que tu es incapable de prouver leurs théorèmes, c'est faux, c'est seulement dans ta tête !

**mehdi_128** · 03/10/2018, 19h27

Les maths de L1 sont 100 fois plus difficiles que les maths de terminale déjà.

Ansset a compris ce qui me gênait ! D'accord ça marche bien avec le epsilon' < Min(alpha,epsilon)

Le début de la démo

invite51d17075 · 03/10/2018, 20h05

j'ai aussi pointé une autre coquille si tu te souviens.
mais le soucis , c'est qu'avec un livre pareil , tu finis par ne plus raisonner ( comme dans ton post #12 )
donc tu t'embrouilles parfois et comme par ailleurs tu y rajoutes parfois tes propres erreurs ( cela peut arriver ).
ben, tout devient confus et difficile de te répondre proprement.

franchement, change de "bible" , tout le monde y perd son temps, tu ne crois pas ?

**mehdi_128** · 03/10/2018, 20h12

Je pense que dans les livres où les démos sont expliquées avec 3 fois moins de détails je comprendrai encore moins. C'est le cas de la majorité des livres du supérieur.

Au moins dans ce livre je capte la logique des démos même si parfois je bloque sur un point.

Mais y a qu'à regarder les cours sur internet, je comprends rien aux démos. Pas détaillées et trop tordues.

**mehdi_128** · 03/10/2018, 23h01

Sinon une dernière question.

Si on a : ]a,b[ c I et f strictement croissante sur I avec a < x < b

Peut on écrire : f(a) < f(x) < f(b) ?

invite6710ed20 · 03/10/2018, 23h29

Bjr
Tiens j'ai déjà vu cette question ailleurs.

https://forums.futura-sciences.com/m...eciproque.html

https://www.maths-forum.com/superieu...e-t198131.html

https://www.ilemaths.net/sujet-intervalle-793941.html

Quelqu'un peut-il lui donner l'adresse d'un autre forum?

invite51d17075 · 03/10/2018, 23h57

Envoyé par mehdi_128

Sinon une dernière question.

Si on a : ]a,b[ c I et f strictement croissante sur I avec a < x < b

Peut on écrire : f(a) < f(x) < f(b) ?

si tu prend un intervalle ouvert , la fonction n'est pas définie en a , ni b.

invite9dc7b526 · 04/10/2018, 08h52

tiens, personne n'a tiqué sur ça:

Soit f une fonction continue et strictement monotone sur un intervalle I.

une bijection continue sur un intervalle I est forcément strictement monotone il me semble.

**gg0** · 04/10/2018, 09h34

Effectivement,

mais à ce stade du bouquin, ça n'a peut-être pas encore été démontré.

Cordialement.

**mehdi_128** · 04/10/2018, 12h26

Envoyé par minushabens

tiens, personne n'a tiqué sur ça:

une bijection continue sur un intervalle I est forcément strictement monotone il me semble.

Oui on utilise cette propriété dans la démo que je vous ai montré pour l'équivalence :

$\text{[math]}$

Ce n'est pas expliqué dans mon livre, mais je pense que pour montrer que l'inégalité de gauche implique celle de droite il faut utiliser la stricte croissance de $\text{[math]}$ sur $\text{[math]}$

**mehdi_128** · 04/10/2018, 12h28

Envoyé par ansset

si tu prend un intervalle ouvert , la fonction n'est pas définie en a , ni b.

Donc je faisais bien de me prendre la tête

**mehdi_128** · 04/10/2018, 12h38

Soit $\text{[math]}$ une fonction continue et strictement monotone sur un intervalle $\text{[math]}$ .
Alors la bijection réciproque $\text{[math]}$ de $\text{[math]}$ est strictement monotone sur $\text{[math]}$ et de même sens de variation que $\text{[math]}$ .

Cette démo est facile, je peux même la faire tout seul.

Supposons $\text{[math]}$ strictement croissante sur $\text{[math]}$ .
Soient $\text{[math]}$ tels que $\text{[math]}$
$\text{[math]}$ est strictement monotone et continue sur $\text{[math]}$ donc $\text{[math]}$ est bijective et admet une bijection réciproque.

Notons : $\text{[math]}$ et $\text{[math]}$

On a ainsi : $\text{[math]}$

On en déduit que : $\text{[math]}$

Finalement $\text{[math]}$ est strictement croissante sur $\text{[math]}$

**mehdi_128** · 04/10/2018, 13h36

J'ai une question pour la continuité parfois l'auteur utilise :

$\text{[math]}$

Ou :

$\text{[math]}$

Il y a équivalence ?

**gg0** · 04/10/2018, 13h45

Démontre-le. C'est un exercice de L1 (donc de capes).

**mehdi_128** · 04/10/2018, 14h05

L'implication :

$\text{[math]}$

est évidente car l'inférieur stricte implique le inférieur ou égal.

Montrons :

$\text{[math]}$

Soit : $\text{[math]}$

Prenons : $\text{[math]}$

Prenons : $\text{[math]}$ ce eta' dépend de eta.

$\text{[math]}$

Ceci est valable pour tout $\text{[math]}$ car $\text{[math]}$

Bijection réciproque

Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Re : Bijection réciproque

Discussions similaires

bijection réciproque

bijection réciproque

Bijection réciproque

bijection réciproque

bijection et réciproque