Tangente commune a deux polynômes

[Lynskyn]

Bonjour,

J'aurais besoin d'un coup de main pour réaliser un programme en VBA.
Voici le problème:

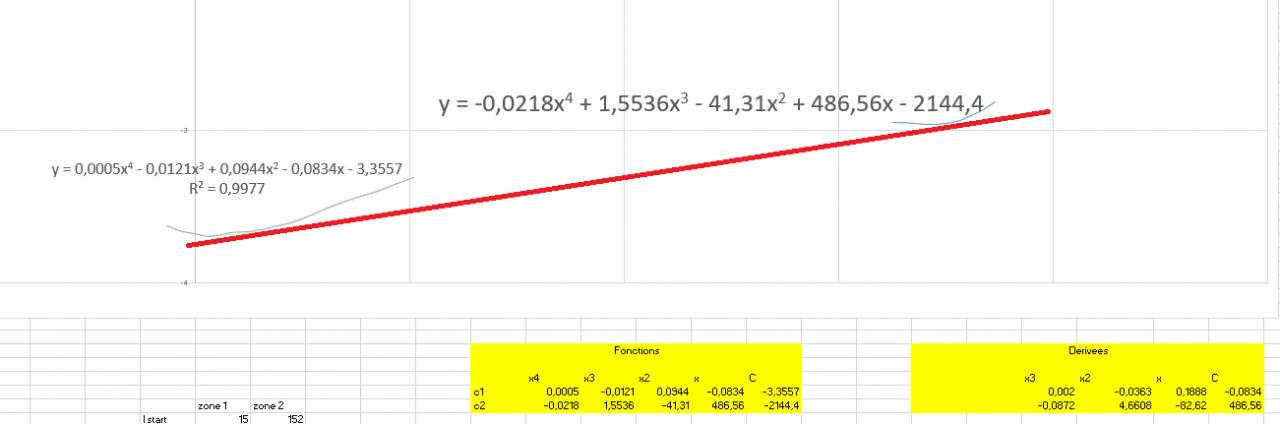
J'ai deux polynômes f(x) et g(x) trouvés a partir de régressions faites par Excel. Je veux trouver l’équation de la tangente qu'ils partagent (en rouge), graphiquement ça ressemblerait a ça:


Je suis parti comme cela:
Deux équations de tangentes, les pentes doivent être les mêmes donc f'(a)=g'(b)
Les ordonnées a l'origine aussi donc -f'(a)*a+f(a)=-g'(b)*b+g(b)

Deux équations deux inconnues a et b (les deux abscisses de tangence) ça me semblait pas trop déconnant mais j'ai du rater quelque chose parce que le solveur Excel n'arrive pas a trouver de solution.

Systeme
f'(a)-g'(b)=0
-f'(a)*a+f(a)+g'(b)*b-g(b)=0

variables a et b
cible: première équation = 0
contrainte: seconde équation = 0

Ça doit pas être très complique mais je manque de pratique en maths...

Merci a ceux qui sauront m'aiguiller.
-----

[gg0]

Bonjour.

Si tes polynômes sont ceux qui figurent sur le dessin, tu as
* Une équation à deux variables de degré 3
* Une équation à deux variables de degré 4
Même si les variables sont séparées, la résolution d'un tel système est bien trop complexe pour être menée à bien : la méthode générale est de trouver b en fonction de a à l'aide de la première équation (sais-tu résoudre les équations de degré 3 dans le cas général ?) puis de remplacer dans la deuxième. Tu vas trouver une équation où, en plus du degré 4 en a, il y a des racines cubiques portant sur des expressions en a, voire du calcul trigonométrique ...

Cordialement.

[Lynskyn]

Effectivement ce sont les polynômes en question mais ils peuvent changer en fonction de mes données mesurées.

Je vois que cela va bien au delà de mes compétences malheureusement... Je vais réfléchir un peu pour voir si je peux procéder différemment pour accéder à cette équation de droite

En tout cas merci pour ces premiers éléments

[feanorel]

Surtout j'ai un doute que ce soit ce que tu cherches :
une regression polynomiale sera assez sensible aux données,
et une tangeante commune, si elle existe y sera encore plus sensible.

Que cherches tu exactement ?

[A voir en vidéo sur Futura]

[Lynskyn]

Finalement j'ai résolu le système en définissant deux fenêtres d'abscisses et définissant un pas de calcul des équations. Cela corrèle bien avec l'outil actuel. Problème résolu.
Merci d'avoir pris le temps

[Surlin Luc Rodes]

Je ne comprend pas cette exercice.

[ansset]

bjr, à quoi correspond la courbe en noir ?