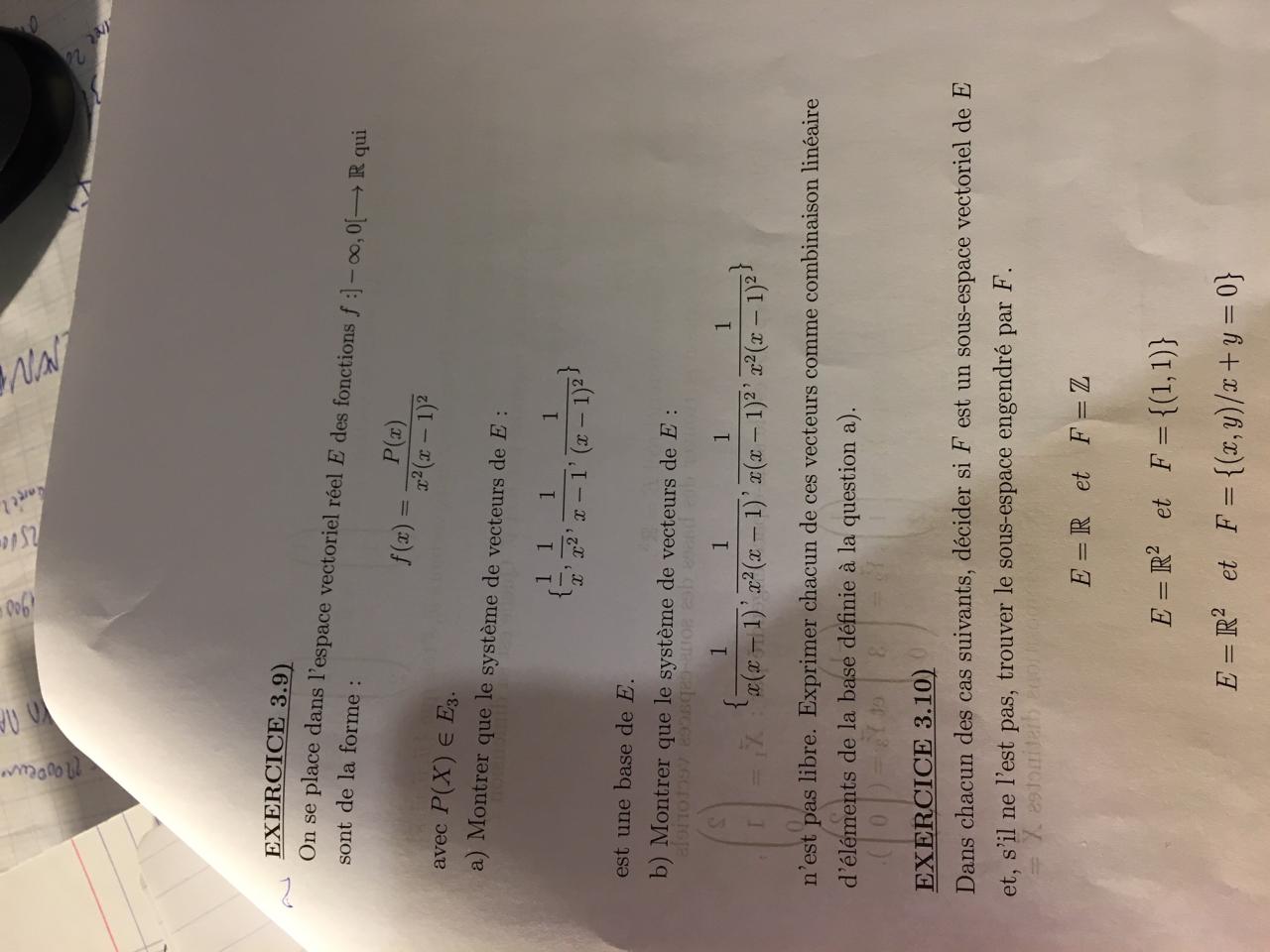Bonsoir ,
j'avais une question par rapport à l'exercice 3.12.
Pour répondre à la question sur les bases des sous espaces vectoriels, le prof a trouvé comme base : F = vect(X1, X2) = {(x,y,z) ϵ R^3 / x - 2y + z = 0}
G = vect(Y2, Y3) = {(x , y, z) ϵ R^3 / 3x + y - 2z = 0}
Pourquoi avoir choisi X1 et X2 pour la base de F et Y2 et Y3 pour la base de G?
On peut avoir une infinité de bases nan ?
Merci à vous.
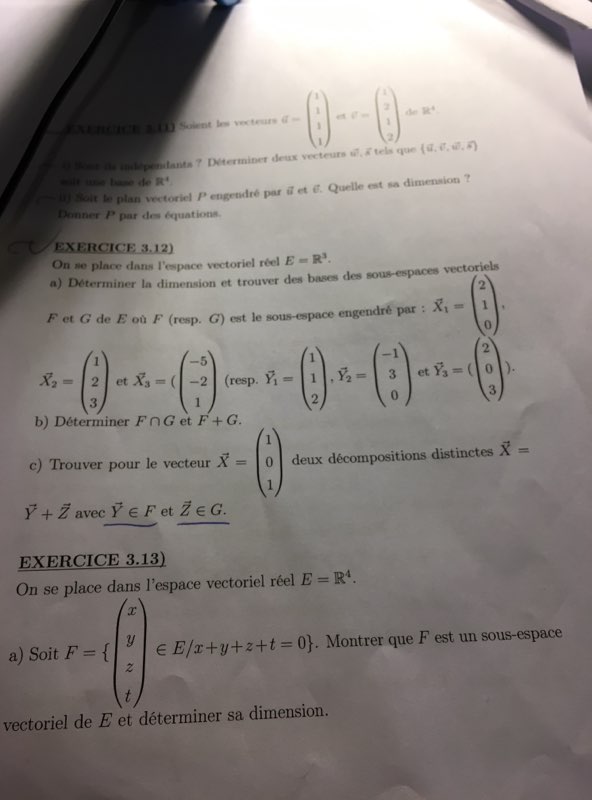
Il y a souvent (et notamment ici) une infinité de bases possible mais l'exercice demande de trouver des bases, donc on peut choisir celles que l'on veut. Au passage je suis surpris de voir qu'on écrit encore les vecteurs avec des petites flèches sur la tête...
Bonjour Momo54500.
Quand on a une famille liée de trois vecteurs dont aucun n'est multiple d'un autre (donc deux à deux, ils sont linéairement indépendants), chauqe couple de ces vecteurs forme une base du sous-espace engendré. Tu peux le prouver facilement.
Cordialement.
Bonjour,
je vous remercie pour vos réponses.
Donc on aurait également pu prendre les vecteurs X2 et X3 pour et Y1 et Y2 pour G?
Merci à vous.
oui,
il suffit de prendre 2 vecteurs non-colinéaires pour chaque sous espace vectoriel. ( chacun devant app à cet espace )
Okay je vous remercie.
Ou sinon j'avais également un problème avec l'exercice 3.9. C'est la première fois que je vois un polynome associé à ce chapitre.
Vous savez par ou commencer pour ce genre d'exercices?
Merci à vous
Le prof a résolution en faisant :
P(x)/(x²(x-1²)) = alpha/x + B/x² + gamma/(x-1) + delta/(x-1)²
Puis il a fait :
( alpha/x + B/x² + gamma/(x-1) + delta/(x-1)² ) = 0
alpha*x*(x-1)² + beta(x-1)² + gamma*x²*(x-1) + delta * x² = 0
donc alpha = beta = gamma = delta = 0
donc dim F = 4 .
Je n'ai pas bien compris son raisonnement sauf la décomposition en éléments simples mais je ne vois pas l'utilité.
Merci à vous.
Dernière modification par Momo54500 ; 25/03/2019 à 12h16.
Il suffit de montrer que cette famille est libre (la preuve de ton prof) et génératrice. Pour génératrice, il faut connaître la méthode de décomposition en éléments simples, que ton prof utilise sans le dire (ou tu n'as pas entendu).
Cordialement.
