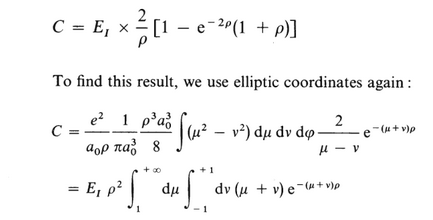Bonjour,
Je bloque sur la résolution d'une intégrales dans un livre:
Pièce jointe 413188
avec
Pièce jointe 413187 et 9.png
Or il se trouve que la fonction 8.png n'admet pas de solution.
Je ne sais pas comment ils ont trouvé la solution a cette intégrale.
C.C. Tannoudji, B. Diu, F. Laloe, quantum mechanics volume 2, page 1176
Cordialement,
napoleondynamique
Dernière modification par albanxiii ; 19/05/2020 à 11h49. Motif: correction du titre
"Pièce jointe spécifié(e) non valide. Si vous suivez un lien valide, veuillez notifier l'administrateur"
*Je bloque sur la résolution d'une intégrales dans un livre:
Note : on résout une équation, on calcule une intégrale, mais pas de mélange entre les deux.
On vous dit d'utiliser les coordonnées elliptiques : https://fr.wikipedia.org/wiki/Coordo...es_elliptiques ça n'est pas très connu, mais ça sert ! (pour faire le changement de variable dans l'intégrale il faut faire comme d'habitude, avec les différentielles et le jacobien).
Dernière modification par albanxiii ; 19/05/2020 à 11h52.
Not only is it not right, it's not even wrong!
albanxiii merci pour la réponse mais je pense avoir mal expliqué mon problème.
J'ai bien sur essayé de résoudre cette intégrale avec les coordonnées elliptique sauf qu'il me mène a une intégrale impossible a calculer (la fonction est divergente).
avec
1<u< infinie
-1<v<1
0<φ<2π
Bonjour,
Vos manipulations de produits sous la somme sont aberrantes! Cela ne marche pas comme cela
Les constantes peuvent sortir du signe somme, mais si c'est un produit de fonctions, il faut faire une intégration par parties, et en aucun cas faire le produit des deux intégrales
PS : ce que vous avez fait en premier n'est PAS une intégration par parties, mais un simple changement de variables
Dernière modification par Resartus ; 19/05/2020 à 18h07.
Why, sometimes I've believed as many as six impossible things before breakfast
