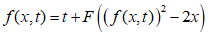Bonjour, cette EDP semble simple mais je n'arrive pas à la résoudre :
Cette équation ressemble à l'équation de Burgers sans viscosité.
On peut trouver des solutions avec la méthode des caractéristiques, mais les solutions sont implicites, auriez-vous une méthode s'il vous plaît ?
Quelle que soit la méthode la solution générale de l'EDP sera obtenue sous la forme d'une équation implicite :
dans laquelle F est une fonction arbitraire tant qu'il n'y a pas de condition initiale spécifiée.
Note que cette unique solution générale peut être écrite sous forme d'un grand nombre d'équations implicites mais qui sont toutes équivalentes même si cela n'apparaît pas à première vue.
Mais, de toute façon, vous n'échapperez pas à une équation implicite pour exprimer la solution générale.
Ceci par ce que l'énoncé de la question ne spécifie pas une condition initiale (ou autre condition).
Selon la condition initiale donnée, il devient possible (ou non) de déterminer explicitement (ou non) la fonction F. En reportant cette fonction dans la solution générale ci-dessus, on obtient une équation qui peut (ou non) être résolue pour trouver la fonction f qui satisfait à la fois l'EDP et la condition imposée.
Bien entendu, lorsque le calcul explicite suggéré ci-dessus est analytiquement impossible, il faut se contenter de la solution implicite qui est tout aussi valable que si on avais pu l'exprimer explicitement, mais qui peut être plus difficile à utiliser en pratique pour du calcul numérique.
Bonjour, je te remercie pour ta réponse, du coup ça me rassure ^^
Par ailleurs je trouve
En effet, en partant de
Par identification à :
J'obtiens :
et donc
t(s)=s pour t(0)=0
x(s)=f(x,t)*s+Xo avec x(0) = Xo
et donc f(x,t)=s+C
Mais comme s=t , et en prenant pour condition initiale à t=0, F(Xo,0)=C, donc :
Peut-être que je me trompe, je voudrais bien savoir comment tu t'y prend s'il te plaît ^^
Mais j'ai une dernière question que me tracasse, si F(Xo)=sin(Xo) en condition initiale, par conséquent la solution générale est f(x,t)=t+sin(x-f(x,t)*t).
Il faut donc résoudre cette dernière équation afin de trouver f(x,t) ??
Il semble que f(x,t)=t+F(x-f t) n'est pas solution de l'EDP. En reportant cette fonction dans l'EDP on constate que l'équation n'est pas satisfaite. Pour le moment je n'ai pas le temps, mais je reviendrai sur ce problème.
merci beaucoup en tout cas ^^
Voir la méthode des caractéristiques : https://en.wikipedia.org/wiki/Method...ntial_equation
Dernière modification par JJacquelin ; 27/08/2020 à 11h15.
Il est toujours utile de vérifier si la solution trouvée satisfait bien l'EDP.
L'erreur dans votre calcul est içi :
C'est tellement bien expliqué, je suis très content ^^
Du cours, à la résolution en passant par la vérification tout y est. Et cerise sur le gâteau vous me permettez de comprendre mon erreur.
Vous devez être un sacré bon prof de maths !
Je vous remercie beaucoup ^^
J'ai une dernière question du coup ^^ (désolé d'abuser mais je ne demande qu'une piste)
Je débute dans le domaine des EDPs, il y a peu de ressource sur internet concernant cette question, pas de livre dans les bibliothèques.
Je souhaite résoudre ce système d'EDP :
En utilisant la méthode que vous venez de m'enseigner, j'obtiens :
En multipliant les combinaisons d'équations différentielles caractéristiques et en vérifiant les solutions je n'obtiens rien de bon.
Peut être que la méthode des caractéristiques ne s'applique pas à ce genre de système.
Quelle technique dois-je utiliser à votre avis ?
Tout d'abord il y a probablement une faute de dactylographie dans les deux EDP (f au lieu de t au dénominateur).
Effectivement ce n'est pas si simple. Dans ma réponse, c'est une version "simpliste" de la méthode parce que cela était valide dans ce cas là. Mais il ne faut pas appliquer une "recette" sans connaitre les ingrédients, en l'occurrence sur quoi la recette est fondée. Il faut d'abord maîtriser la théorie pour ne pas l'appliquer à mauvais escient. Au début de ma réponse il y a une référence à un article pour en apprendre sur le sujet. Et ne pas bruler les étapes.
Le cas d'un système de deux PDEs, tel que celui proposé, est tout autre. Ce n'est plus du tout une question similaire à celle qui était posée au départ. Je pense donc qu'il vaudrait mieux ouvrir une nouvelle discussion pour éviter les confusions. Et ne pas trop en espérer car, en pratique, dans les cas compliqués on résout le problème par des méthodes de calcul numérique au lieu de calculs analytiques. Bonne chance.
Oui effectivement il y a une faute au dénominateur, c'est t au lieu de f.
En effet, j'essaie peut-être d'aller trop vite, et du coup je mélange tout ^^
Merci beaucoup pour vos explications en tout cas, je maîtrise un peu mieux cette technique !
