Coordonnées GPS, mille nautique, cercle.. problème réel urgent*!

[invitecd41c164]

Bonjour à tous ! Un passage très bref pour vous montrer comment ça fonctionne :



Merci merci vous ne vous rendez pas compte à quel point ça nous facilite la tâche !

à très vite
-----

[Biname]

Salut,
Merci pour le feedback ... et tous les mercis !
Fais-nous un petit coucou depuis la passerelle
Biname

[invite12e4e957]

C' est bon ! On n' a toujours pas perdu Cocolastic

[Biname]

Salut,

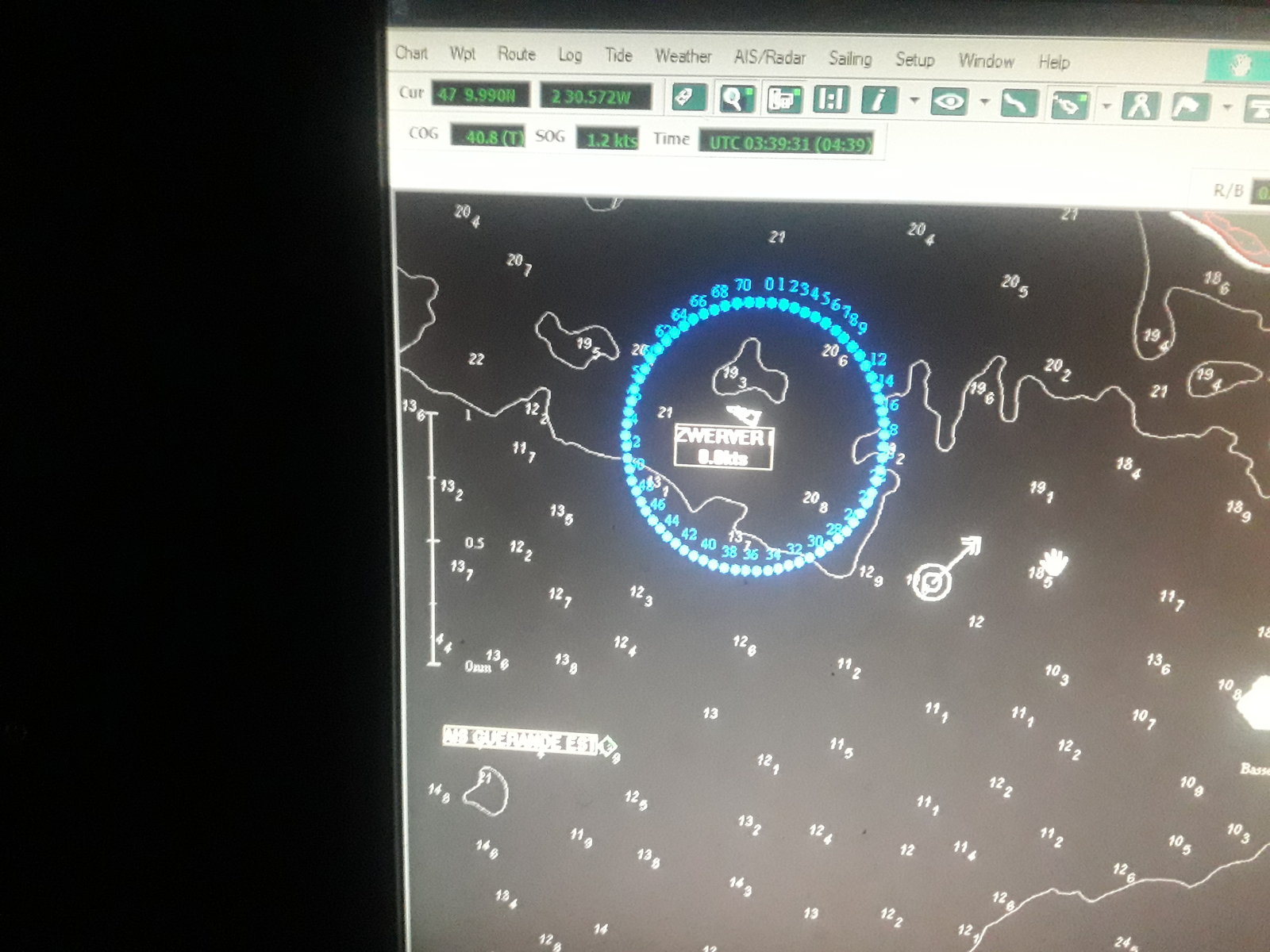
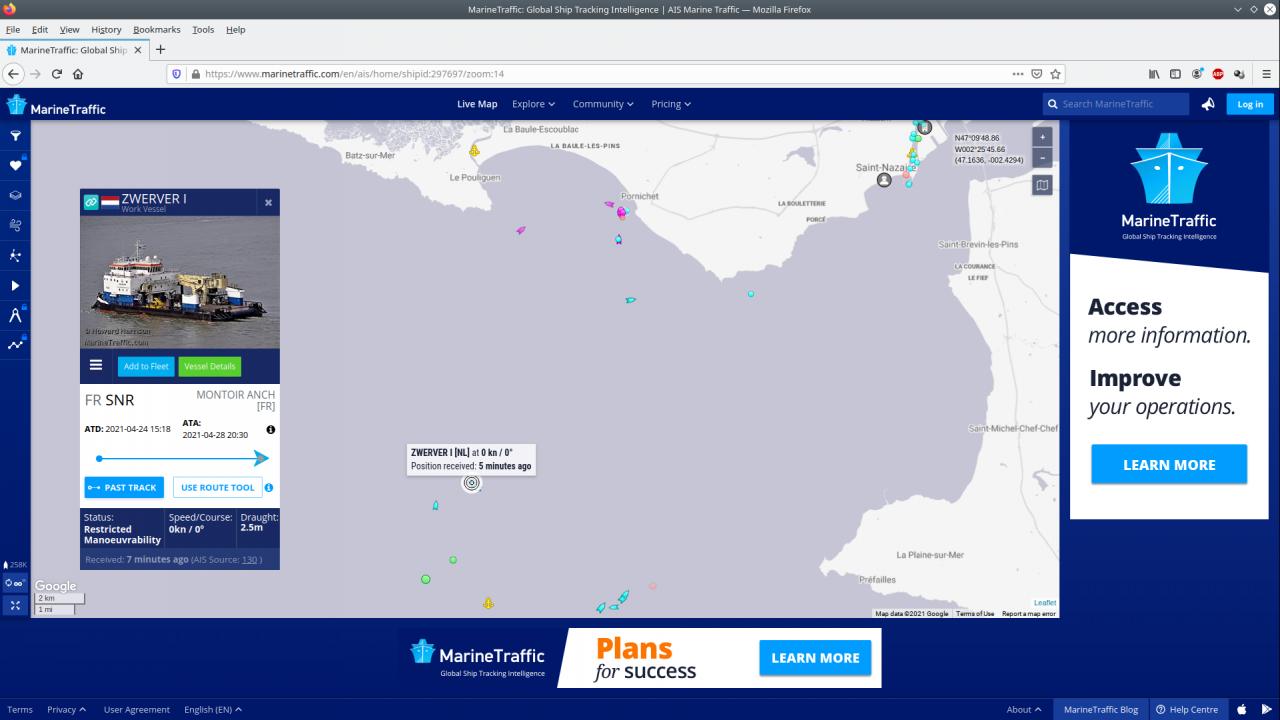
L'activité de ce bateau doit être liée à la construction du 'champ éolien de Saint-Nazaire'(480MW !), juste un poil à l'ouest de notre point.

Sur VesselFinder plutôt que Marine Traffic, l'affichage en fond des cartes marines Navionics est possible ainsi que le tracage des points à une certaine distance d'un autre (le ?compas en haut à gauche de la fenêtre).

Difficile de croire qu'à bord de ce bateau, il n'y avait pas _au_moins_ une personne capable de faire ce qu'on a fait ! Remarquez, faut en avoir le courage, au premier coup d'oeil, on pense à la trigonométrie sphérique et à ses très nombreuses(2) formules et angles ... qu'on ne sait plus très bien : on en a pour un bon bout de temps. Ici, c'est en deux temps, deux cerveaux qu'on est arrivé à la solution.

1 - OBI msg #2 et #4 fait l'approximation salvatrice mais, pas marin?(1), il commet une erreur. Il nous sort de la trigonométrie sphérique : ouf !
2 - Chadok corrige et, aidé par Python, nous sort des points.

Biname

(1) un marin eut été inhibé car il sait que les échelles longitude/latitude diffèrent ?
(2) https://studylibfr.com/doc/790377/tr...sph%C3%A9rique complet

[obi76]

1 - OBI msg #2 et #4 fait l'approximation salvatrice mais, pas marin?(1), il commet une erreur. Il nous sort de la trigonométrie sphérique : ouf !

Oui non c'est vraiment une erreur bête. J'avais "juste" oublié de visualiser l'impact du premier angle sur l'arc que fait le second en sphérique (fatigué...)

[Biname]

Salut,

Oui non c'est vraiment une erreur bête. J'avais "juste" oublié de visualiser l'impact du premier angle sur l'arc que fait le second en sphérique (fatigué...)

Erreur ! Je ne m'autorise pas à jeter la première pierre

Si tu avais vu, aurais-tu continué ?

Je pense que, sans ton 'erreur', on n'aurait pas fait cette approximation.

Je me demande si cette approximation est connue ? Probablement ?

Personnellement, enfermé/rebuté dans/par la solution lourde de la trigonométrie sphérique, je n'y ai même pas pensé et n'y aurais jamais pensé.

C'est paradoxal, une erreur mène à la solution !

Biname

[obi76]

Ben en fait du coup j'étais occupé par autre chose, parce que c'est une erreur que j'ai faite dans un de mes codes, le fait de l'avoir vue m'a fait passer plusieurs journées pour le corriger (mais c'est un bien). Cette approximation marche très bien près de l'équateur (là où le cos(latitude) est proche de 1), mais est d'autant plus faux que l'on se rapproche des pôles.

Mais effectivement, si ça a été un point permettant de résoudre le problème, ben tant mieux, comme quoi les discutions sur le forum s'avèrent utiles

[invitede656be3]

Bonjour ,
Je vous propose un programme en C++ qui permet peut-être de résoudre votre PB.
Vous entrez les coordonnées du point où vous êtes et la distance maximum ( !!! en km) et vous obtenez les coordonnées des points limites( 180) tels que la distance orthodromique soit inférieure à la distance maximum.
Il marche sous CodeBlock (gratuit et téléchargeable). Il peux facilement se transposer en Python (mais je ne suis pas un virtuose).
Ci-joint le code en Txt à copier sous CodeBlock.

[Biname]

Salut,

Bonjour ,
Je vous propose un programme en C++ qui permet peut-être de résoudre votre PB.
Vous entrez les coordonnées du point où vous êtes et la distance maximum ( !!! en km) et vous obtenez les coordonnées des points limites( 180) tels que la distance orthodromique soit inférieure à la distance maximum.
Il marche sous CodeBlock (gratuit et téléchargeable). Il peux facilement se transposer en Python (mais je ne suis pas un virtuose).
Ci-joint le code en Txt à copier sous CodeBlock.

Ton code est ici où il compile en cliquant sur RUN !
https://www.onlinegdb.com/r1YhrpF_d

Faudrait pas ??au moins?? sur le site çi dessus :
1) commenter les lignes 62,63 et 64 ?
2) ligne 92 changer Angle_Rad_Deg(Lat0, &Long); en Angle_Rad_Deg(Lg0, &Long);

Le site me propose de créer un 'fork' et hop voici la correction
https://onlinegdb.com/B1l5E_qdO

C'est mieux !

Biname

[invitede656be3]

Bonjour,
Il y a effectivement une erreur ligne 92.
Les lignes 62,63 et 64 court- circuitent la saisie des entrées pour la mise au point de PG. Soit on les supprime( //) ,
soit et on entre directement les valeurs sur ces lignes ( en radians et km) après avoir court- circuiter la saisie des entrées( /* */).
Je n'arrive pas à utiliser OnlineGDB.
Je joins une petite modification qui permet d'imprimer sur un fichier ***.txt.

[Biname]

Salut,

Je n'arrive pas à utiliser OnlineGDB.

Je suppose que tu veux rééditer le code, il faut alors créér un 'fork' avec en haut à gauche 'fork this' en vert.
Tu ouvres alors une nouvelle fenêtre avec le code que tu veux éditer modifier et sauver sans effacer le mien, ce sera ton fichier avec son URL, les deux versions restant intactes.
On peut ainsi 'forker' à plusieurs et on crée un arbre de 'forks' ...

Il me semble que tu traces des losanges sur pointe et non des cercles ????????????????????? mais je n'ai pas tout compris ?

Je joins une petite modification qui permet d'imprimer sur un fichier ***.txt.

C++ dès que ça se complique un peu je rame !

Depuis quelques jours, j'essaye de débugger mon code javascript qui utilise la trigonométrie sphérique et non un approximation.
Il fonctionne très bien pour autant que
- un des pôles nord ou sud ne soit pas dans le cercle
- le méridien zero ne traverse pas le cercle,
- ... pb de signe, de cotg et une division par zéro

A vos forks ! https://onlinegdb.com/kVhstzhZN (RHINO Javascript chez eux ... print)

Biname

[invitede656be3]

Bonjour,

La méthode (dichotomie ) que j'utilise est très précise. L'écart est (Ortho0 - R_Rech ) <= 10- 6
On peut même faire plus précis en diminuant Epsilon. On peut aussi augmenter le Nb de pas de calcul de Lat0 (180 actuellement).
Le calcul de l'orthodromie est aussi très précis car se fait avec des "double".
Il y a une autre formule qui donne les mêmes résultats :

double Orthonomie_2(double Long1, double Lat1, double Long2, double Lat2)
{
double c ;
c = acos(sin(Lat1) * sin(Lat2) + (cos(Lat1) * cos(Lat2) * cos(Long2 - Long1)));
return( Rterre * c);
}
Je pense que la précision dépends plus de la valeur que l'on prend pour le rayon de la terre et le fait qu'elle n'est pas vraiment sphérique.

Je ne pense pas qu'on puisse imprimer depuis code block d'où le passage par un fichier .txt.

La courbe obtenue n'est pas un cercle mais une sorte d'ellipse en 3D (Intersection sphère avec cylindre dont l'axe passe par le centre de la sphère).

Si on se rapproche trop des pôles la latitude devient supérieure à Pi/2; le PG indique ECHEC, cela dépend du rayon de recherche.
Il est peut-être possible de faire le calcul en considérant les équations de l'intersection sphère avec cylindre dont l'axe passe par le centre de la sphère et centré sur les pôles mais compliqué: système d'équations du second degrés avec 3 variables.
Par contre RAS pour l'équateur.

[obi76]

La courbe obtenue n'est pas un cercle mais une sorte d'ellipse en 3D (Intersection sphère avec cylindre dont l'axe passe par le centre de la sphère).

Qu'est ce que ça change par rapport aux méthodes qui ont été proposées au dessus ?

[Biname]

Salut,

Qu'est ce que ça change par rapport aux méthodes qui ont été proposées au dessus ?

Ce n'est plus une approximation, on est en math ici, pas en ingé . D'un point de vue pratique, l'approximation est parfaite pour R < ?1000 milles?.
@Omega3.0
Au passage : mes 'cercles polaires' sont nommés des 'petits cercles' par la trigonométrie sphérique et ton l''orthonomie' est plutôt l''orthodromie' (qui s'oppose à loxodromie ...), "Avec le temps va, tout s'en va, ..."
OK, pour ta recherche 'dichotomique'? du point à une distance d du centre en scannant entre ?lat mini et ?lat max ???
Mon calcul(en chantier) fait appel aux formules de trigonométrie sphérique et donne une solution directe.

Biname

[obi76]

Ce n'est plus une approximation, on est en math ici, pas en ingé .

Quand je vois une dichotomie, pour moi c'est une approximation

[Biname]

Salut,

Quand je vois une dichotomie, pour moi c'est une approximation

Oui mais lui, il peut définir une précision, P tel que Rp = R±0.0001 milles par exemple !

Mon code ne présente pas ce problème, il trouve des solutions exactes, il faudrait un peu bosser dessus ... pour les signes ...
https://onlinegdb.com/13pqdOeF8

Biname

[obi76]

Mon code ne présente pas ce problème, il trouve des solutions exactes, il faudrait un peu bosser dessus ... pour les signes ...

La méthode que j'ai donné au départ et qui a été codée (et corrigée) ensuite non plus. C'est pour ça que je ne vois pas trop l'intérêt de faire un truc plus compliqué pour tomber sur le même résultat...

[invitede656be3]

Bonjour,
Orthonomie : désolé j'ai fait du copier coller à partir d'un vieux programme.
J'ai aussi fais une version de calcul direct en inversant la formule de l'orthodromie : orthodromie_2.
Mêmes résultats avec 11 chiffres après la virgule(en radians). Le calcul est sûrement plus rapide avec le calcul direct.
J'ai introduis les 2 valeurs de longitude Lg0 et Lg1 (à latitude constante Lat0) symétriques par rapport au méridien passant par le point central.
Mais je maintiens que rechercher une telle précision ne sert à rien si on ne prend pas en compte le forme réelle de la terre.
(Il faudrait faire varier le rayon de la terre en fonction de la latitude du point central)
J'ai du mal a décortiquer le PG de Bimane qui doit être en Python mais je vais essayer de l'écrire en C++
Mon PG http://www.onlinegdb.com/edit/Uho7X8cFJ

[Biname]

Salut,
@Obi76
Je trouve ton approximation géniale.
Dans ce fil au msg #30, je montre que pour un rayon de 600 milles centré sur Saint Nazaire, l'erreur sur la distance calculée entre le point trouvé et le centre du cercle peut différer du rayon souhaité de 19 milles Ton Code Python sur GDB pour R=600 et vérif
La raison ? Enfiler son vieux ciré et refaire un peu de trigonométrie sphérique et au passage découvrir GDB qui est une merveille pour partager de 'petits' codes.
@Omega3.0
Ton lien renvoie 'Not Found' ! Sur GDB, je 'login' avec mon compte Google.
Mon code est en Javascript version Rhino imposée par GDB. Dernière source sur GDB
pour C++ : tu remplaces 'var' par 'double' et print par ???cout et ce sera presque bon.
Pour ???WSG84, oui.

Biname

[invitede656be3]

Bonjour,
J'ai essayé de tenir compte que la terre est un ellipsoïde (Voir calcul ci joint).
Pour la latitude du centre on calcul un rayon terrestre local par cette formule. Et il sert pour les calculs des 2 méthodes directes et par dichotomie.
Pour voir l'effet je fais le calcul avec les entrées suivantes

Avec correction:
Rterre équatorial = 6378.388 km
Rterre polaire = 6356.988 km
Rterre calcul = 6367.69699 km
Lat_centre = 0.78539816340 Long_centre = 0.15707963268
Lat0_min = 0.71472897158 Lat0_max = 0.85606735521
Rayon de recherche = 450.00 km

Puis sans correction:
Rterre équatorial = 6371.0 km
Rterre polaire = 6371.0 km
Rterre calcul = 6371.0 km
Lat_centre = 0.78539816340 Long_centre = 0.15707963268
Lat0_min = 0.71476560964 Lat0_max = 0.85603071716
Rayon de recherche = 450.00 km

En récupérant le tout sous Excel on peut calculer les différences maximums entre les latitudes et longitudes ce qui donne:
Ecart LAT Max = 3,6638060E-05 radians ECART Long Max = 5,1976830E-05 radians
Rapporter en distance 3.66 10-5 radians >> 233 mètres en latitude.
On a donc intérêt à faire la correction car les position GPS sont plus précises.
Le PG actualisé est disponible : Online GDB :https://onlinegdb.com/nLwPYuTHx

[Biname]

Salut,
Merci ! Je me suis efforcé à décrypter ton code qui calcule le rayon de l'ellipsoïde WSG84 au centre du cercle recherché.

Je viens de faire une recherche avec "distance between two point on an ellipsoïd", fastoche
on trouve aussi https://en.wikipedia.org/wiki/Vincenty%27s_formulae
Gépatoulu mais là on échappera pas au calcul dichotomique pour trouver les coordonnées du point à une distance d d'un autre.

Et merveille, un code en Python qui fait le boulot : comparer la distance entre deux points pour 'ellipsoïde et sphérique' :
https://www.johndcook.com/blog/2018/...roid-distance/
Pas résisté : le voici sur GDB
Yapluka

Résultats de la recherche :
https://www.google.com/search?q=dist...n+an+ellipsoid

Biname

[Biname]

Un petit plus
Et avec 'Vincenty' on trouve tout ce qu'on veut dont du/des codes C++, ...
Biname