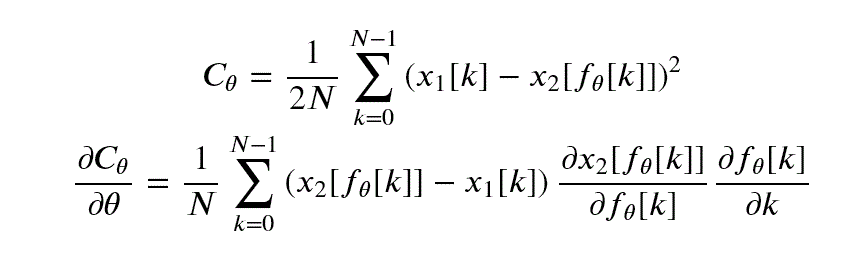Bonjour,
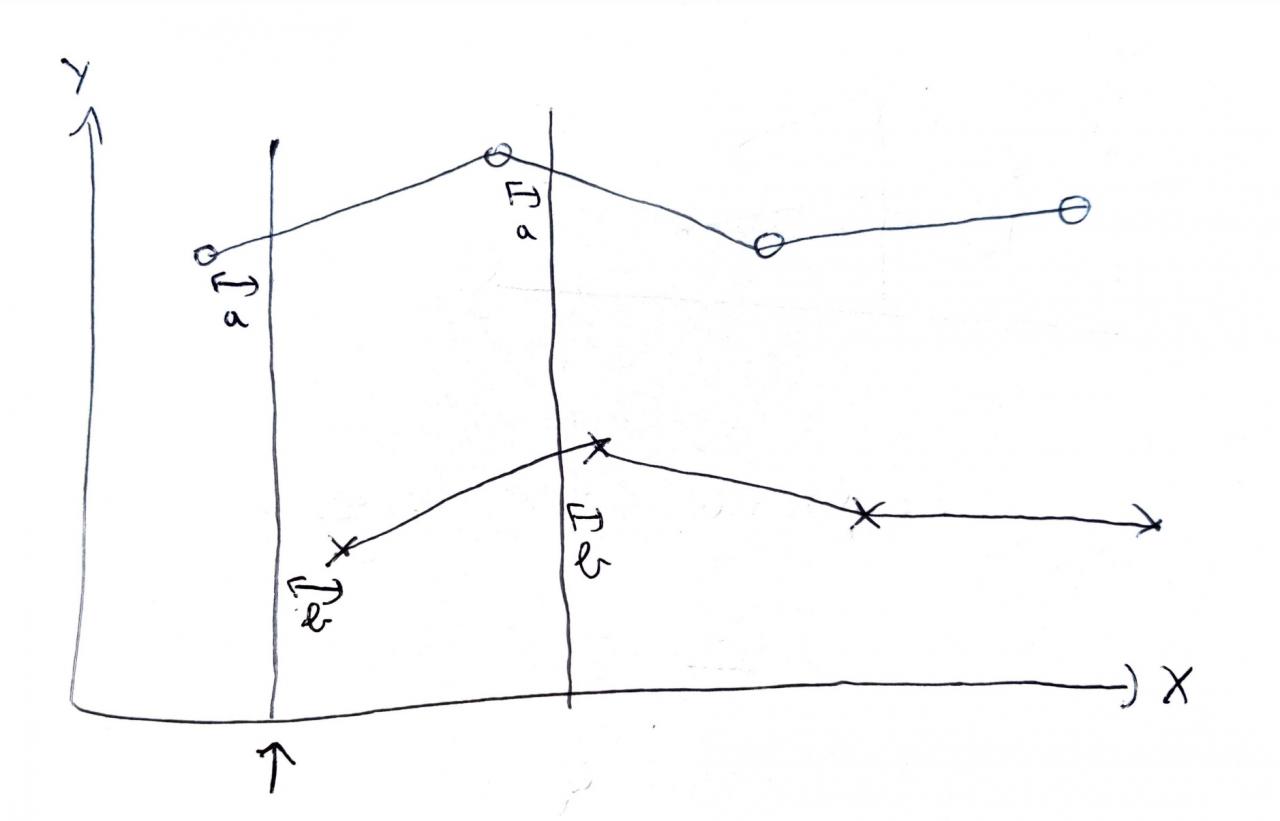
J'ai deux jeux de données que je trace en fonction du temps.
Les points de chaque donnée ne sont pas aligné or j'ai besoin de récupérer pour une valeur de temps X donné, un point de chaque jeu. Pour cela, j'ai besoin d'extrapoler.
Pour ce faire, j'ai besoin de trouver le temps X qui minimise a et b (sur le dessin) entre chaque point pour tous les points.
Cela me permettra d'avoir pour un temps donnée, un point pour chaque jeu de donné.
Pouvez-vous m'aider ?
Merci
-----