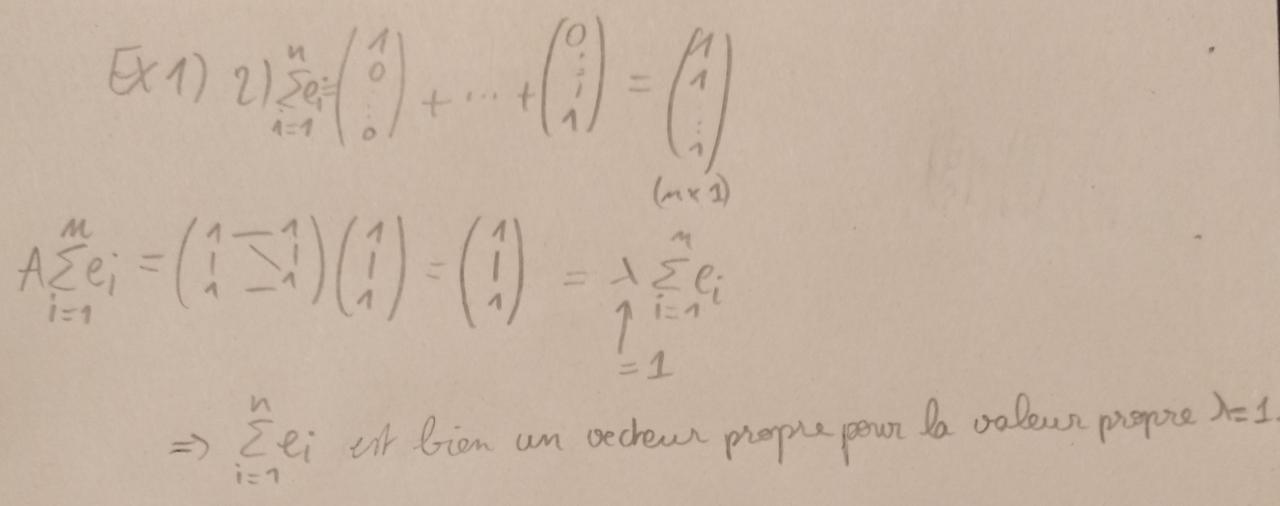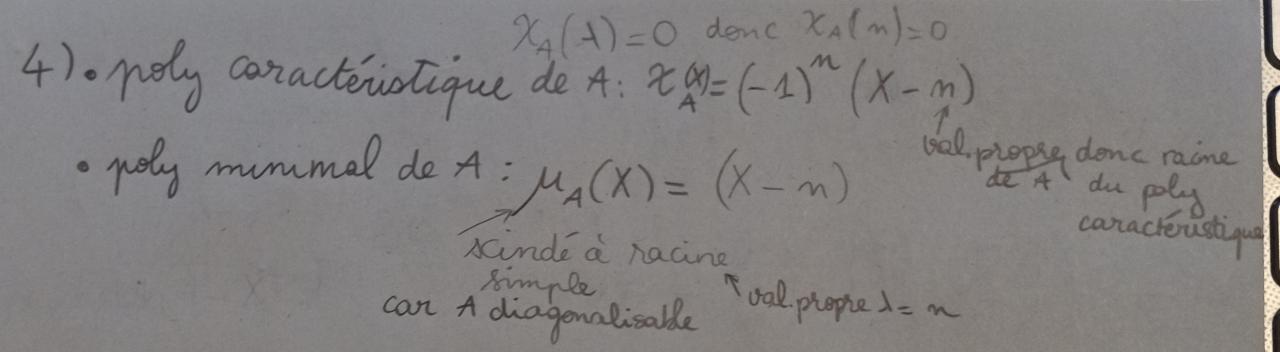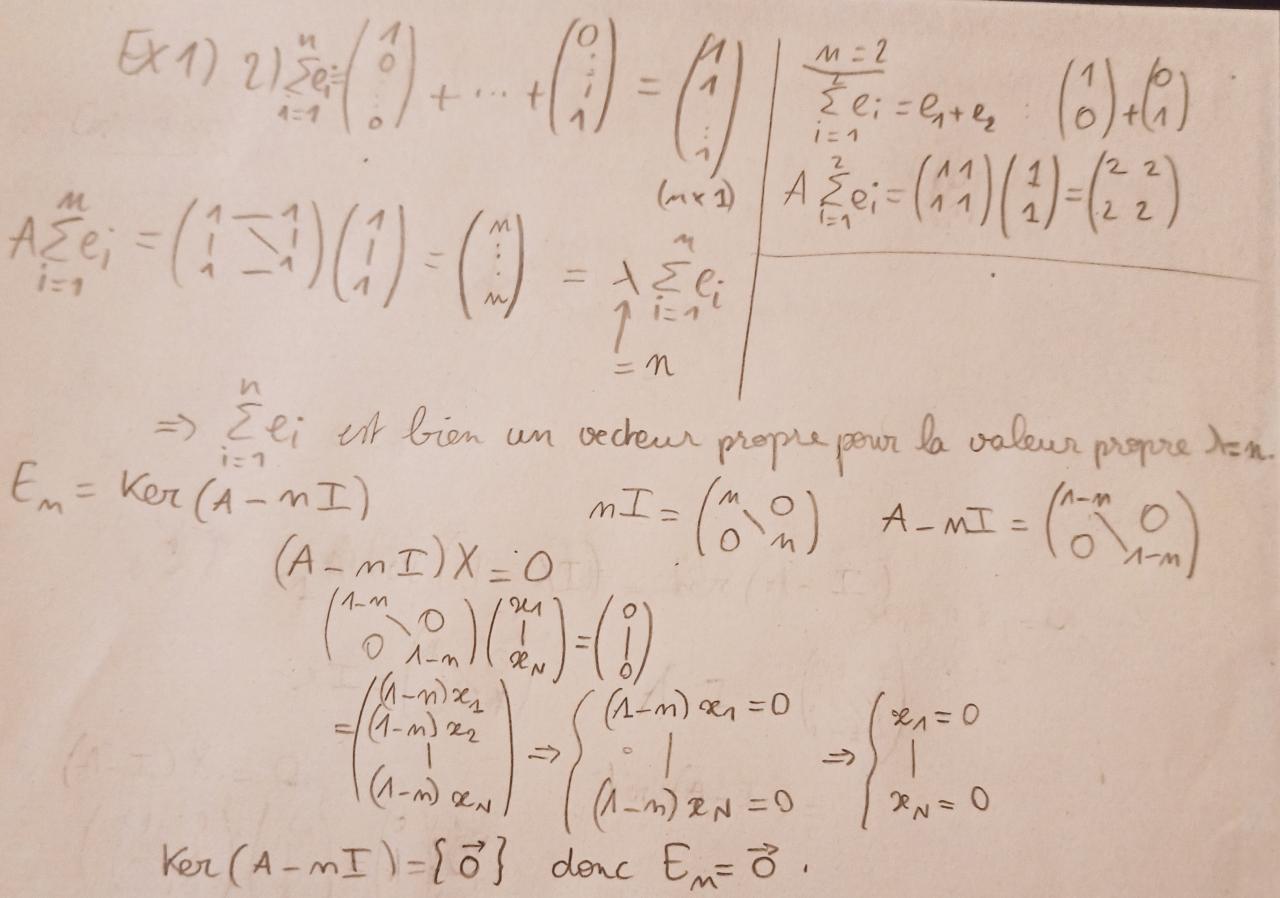Exercice matrice diagonalisable

[math47]

Bonsoir,

J'ai un exercice à faire dont voici l'énoncé :
Capture d’écran 2021-11-29 204847.jpg

1. Voici ce que j'ai fait, qu'en pensez-vous ?
1638217026208.jpg

2. Qu'est-ce que c'est la base naturelle de R ? C'est la base canonique ?

3. En voyant les éléments que j'aurai : faudra-t-il que j'utilise que f est diagonalisable est équivalent à n = somme de i = 1 à r de la dim(Eλ), Eλ étant le sous-espace propre associé à λ et λ étant la valeur propre que je dois trouver à la question 2 ? Qu'en pensez-vous ?

Merci d'avance,
Bonne soirée
-----

[jacknicklaus]

Bonjour,

pour t'aider à compter correctement les vecteurs qui engendrent Ker(A), je te conseille d'utiliser (x1,x2,...,Xn) et non x,y,...,t. Tu verras alors ton erreur.

[gg0]

La base naturelle de R^n (et pas de R) est effectivement la base canonique. Elle est dite naturelle car le n-uplet des coordonnées de x, un vecteur de R^n, est justement x.
Autre chose : n comme dimension, ça devrait immédiatement te faire réagir, voir que ker(A)=R^n, donc que A est la matrice nulle donc ...
C'est un raisonnement qui devrait déjà être automatique.

Cordialement.

[math47]

Pourquoi ker(A)=R^n implique que A est la matrice nulle ?

[A voir en vidéo sur Futura]

[math47]

Merci jacknicklaus, j'ai corrigé qu'en pensez-vous?
IMG_20211130_104317.jpg

PS : Pas besoin de regarder les images attachées je n'ai juste pas réussi à les enlever

[jacknicklaus]

Pourquoi ker(A)=R^n implique que A est la matrice nulle ?

Tu as une matrice carrée A telle que A(v) = 0 pour tout v, et tu ne vois pas pourquoi A serait une matrice nulle ???

[math47]

Voici ce que j'ai fait pour la question 2, qu'en pensez-vous ?

[gg0]

Ton calcul matriciel est complétement faux. Fais-le correctement pour n=2.

Cordialement.

[math47]

J'ai corrigé la question 2 et voici ce que j'ai fait pour la question 3, qu'en pensez-vous ?

[math47]

En espérant que les 3 premières réponses soient justes, voici ce que j'ai fait pour la 4 :


Qu'en pensez-vous ?

[gg0]

Je n'ai rien compris à ce que tu fais à la question 3. Tu démontres (c'est ce qu'il semble, puisque tu le conclus à l'avant dernière ligne que dim(E1)=dim(E1), ce qui ne nécessite pas tous ces calculs, puis tu reprends l'absurdité déjà faite avant que dim(E1)=n !!
Une preuve de diagonalisabilité de A serait soit une diagonalisation, soit l'utilisation d'un théorème qui la prouve. Tu rédiges des calculs dont on ne sait pas où ils vont ... Quel moyen de preuve veux-tu utiliser ? Quel théorème ? Il doit apparaître dans ta preuve, sous la forme de la satisfaction de toutes ses hypothèses.

Pour la 4, le polynôme caractéristique est manifestement faux (tu devrais le voir !!! apprends ton cours).

[math47]

Pour la 3, je voulais utiliser que À diagonalisable est équivalent à : somme directe des Eiλ = E
Ici on a qu'un Eλ donc pas de problème d'intersection et dim(Eλ) = n = dim (R^n) donc somme directe Eλ = R^n => A diagonalisable

[gg0]

Tu pédale dans la semoule !!
Il y a plusieurs valeurs propres de A, donc tu racontes n'importe quoi ! Et tu continues à utiliser dim ker(M) = n qui dit que la matrice M est nulle, cette fois avec A-I. Tu ne réfléchis pas, tu ne tiens pas compte de ce qu'on t'a expliqué ... Crois-tu vraiment que A-I est nulle ?????
S'il te plaît : Un peu de réflexion sur tes erreurs, c'est pénible de devoir reprendre sans arrêt la même explication basique (la notion de dimension se voit généralement tout au début).

[math47]

Alors on va reprendre depuis la question 2 : on me demande une valeur propre, selon vous il y en à plusieurs, je dois alors toutes les donner ?
Toujours sur la question 2 : mon calcul de A.somme de I=1 jusqu'à n des ei est correct ou non ?

[gg0]

A la question 2, on ne te demandait d'utiliser un vecteur pour trouver une valeur propre, tu y a répondu. Mais c'est être bien naïf que de croire que parce qu'on a trouvé une valeur propre il n'y en aurait pas d'autre. En fait, dans la question 1 on t'a fait trouver indirectement une autre valeur propre (sauf dans un cas particulier).
Le calcul de la question 2 est maintenant correct, n est bien une valeur propre. Quel est l'espace propre associé ?
Indication : penser ensemble les questions 1 et 2.

[math47]

Voici ce que j'ai fait pour trouver l'espace propre associé :

Qu'en pensez-vous ?

La valeur propre que l'on trouve indirectement à la question 1, c'est 1 ?

[jacknicklaus]

Tu fais erreur. la matrice (A - nI) n'est pas une matrice diagonale avec des (1-n) .
que sont devenus les 1 de A en position non diagonale ?

[gg0]

1) Tu as repris un calcul déjà fait. Inutile.
2) Tu as donc un vecteur propre, non nul, puis tu "démontres" que l'espace propre associé ne le contient pas ! Avant de me demander "Qu'en pensez-vous ?" tu aurais dû lire ce que tu as écrit, et te dire "c'est idiot !"

Bon, il est temps pour toi de reprendre sérieusement l'apprentissage de tes leçons, peut-être même en revoyant les bases de l'algèbre linéaire (L1).
Tu écris des énormités et tu ne connais pas assez tes leçons pour t'en rendre compte. manifestement, tu n'as pas compris ce qu'est un espace propre, le lien avec la valeur propre, pourquoi l'espace propre associé à n est ker(A-nI), etc.
"La valeur propre que l'on trouve indirectement à la question 1, c'est 1 ? " Pourquoi 1 ??
Qu'as-tu trouvé à la question 1 pour n=1 ? (*) Pour n>1 ? Traduis en français ...(**)

Cordialement.

(*) Cas particulier que tu n'as même pas vu !! D'ailleurs, les matrices 1x1, bof bof !
(**) manifestement, tu ne fais pas le travail de dire en français ce que tu as trouvé, tu confonds mathématiques et cabalistique !! n'écrire que des symboles est souvent signe d'absence de compréhension ... rédige !

[math47]

J'ai recommencé le calcul de l'espace propre En, qu'en pensez-vous ?

[math47]

D'ailleurs l'autre valeur propre de A doit être 0 car ici Tr(A) = n et la trace est la somme des valeurs propres donc 0+n = n = Tr(A), c'est bien ça ?

En revanche comment dire que j'ai su qu'il y avait une 2e valeur propre ? Si vous ne me l'aviez pas dit je ne l'aurais pas vue... Car si je dis on a trouvé la valeur propre n (question 2) et on sait que la trace de A est égale à la somme des valeurs propres donc 0 en est une également ne fonctionne pas... Toutes les matrices n'ont pas 0 en valeur propre, si ?

[CARAC8B10]

Quelle peut bien être ia valeur propre associée à un vecteur propre de ker(A) ?

[math47]

Justement je bloque un peu...

[CARAC8B10]

V est donc vecteur propre associé à la valeur propre 0

[math47]

Oh merci c'est donc la justification correcte ?

[CARAC8B10]

Oui

On aurait pu traiter le problème autrement
A est de rang 1resres
rappel : le rang d'une matrice est le nombre de ses vecteurs colonnes libres. comme ils sonr tous égaux en soustrayant le premier (de gauche) aux n-1 autres il ne reste que le premier, les aurestres étant nuls.
Donc rang(A) = 1 = dim(Im(A))resresresres
dim(ker(A) = n-1 : théorème du rang
Donc il n'y a que 2 valeurs propres et à déterminer.
Le polynôme minimal est donc du second degré.
Et si on a la curiosité de calculer on trouve , est donc un polynôme annulateur de A et est même le polynôme minimal de A car il estt unitaire.
La deuxième valeur propre est donc n.

[CARAC8B10]

Quand je bouge ma souris, ça me met des "res" un peu partout.
Ne pouvant modifier après 5 minutes, je remets le même message mais purgé de ses "res"

Oui

On aurait pu traiter le problème autrement.
A est de rang 1
rappel : le rang d'une matrice est le nombre de ses vecteurs colonnes libres. comme ils sonr tous égaux en soustrayant le premier (de gauche) aux n-1 autres il ne reste que le premier, les aurtres étant nuls.
Donc rang(A) = 1 = dim(Im(A))
dim(ker(A) = n-1 : théorème du rang
Donc il n'y a que 2 valeurs propres et à déterminer.
Le polynôme minimal est donc du second degré.
Et si on a la curiosité de calculer on trouve , est donc un polynôme annulateur de A et est même le polynôme minimal de A car il est unitaire.
La deuxième valeur propre est donc n.

[math47]

Merci de cette réponse détaillée ! J'aimerais cependant quelques précisions : comment à partir de la dim de Ker(A) on sait qu'il y deux valeurs propres ? Et le polynôme minimal est du second degré car il y a 2 valeurs propres justement c'est bien ça ?

[math47]

Mais du coup pour montrer que A est diagonalisable, on peut montrer que n = somme de i = 1 à 2 des dim(Eλi).
Or dim(E0) = dim(Ker(A)) = n-1 donc il faudrait dim(Eλ) = 1 mais ce n'est pas ce que j'ai trouvé avec mon calcul (message #19) où est mon erreur ?

[CARAC8B10]

Im(A) étant de dimension 1 ne peut avoir qu’un seul vecteur propre (correspondant à une unique valeur propre).
Les n-1 vecteurs (propres) de ker(A) correspondent à l’unique valeur propre : n.
Cela fait bien 2 valeurs propres.

[CARAC8B10]

Or dim(E0) = dim(Ker(A)) = n-1 donc il faudrait dim(Eλ) = 1 mais ce n'est pas ce que j'ai trouvé avec mon calcul (message #19) où est mon erreur ?[

Je ne comprends rien à ton message 19 qui est difficile à lire (et je ne suis pas le seul !)

Si tu peux le taper directement sans photo, j'essaierai de l'examiner ...
Tu remarqueras qu'aucun de tes interlocuteurs n'a utilisé l'image d'un texte manuscrit pour ses réponses...