le problème de la fourmi sur un élastique

[pachacamac]

Bonjour,

Suite à une question que j'avais posé sur le forum d'astronomie ( concernant la réception des signaux en provenance de galaxies dont la vitesse de récession a toujours été est est encore supérieure à c), on m'a indiqué que la réponse se trouvait dans le problème de la fourmi sur un élastique.


Une fourmi qui avance à la vitesse d' 1cm/s sur un élastique qui s’agrandit d'1 km par seconde va atteindre le bout de l'élastique.

La démonstration en est faite dans la page wikipédia en lien, mais je n'ai réussi à la comprendre vu mon niveau insuffisant en math

Vu que c'est le résultat le plus contre intuitif que j'ai jamais rencontré en math, je voudrais savoir si quelqu'un(e) pourrait expliquer ce résultat avec des mots et des phrases plutôt qu'avec des équations.


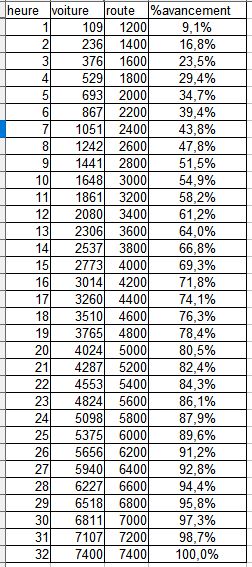
note : j'avais aussi fait une analogie pour me représenter le phénomène en simplifiant les choses, j'imagine une auto qui doit parcourir 1000 km entre A et B et qui roule à vitesse constante de 100 km/h, si pour une raison quelconque B s’éloigne de A à une vitesse supérieure à 100 km/h la voiture n' atteindra jamais B et même elle s'en éloigne de plus en plus.. et donc pour que la voiture puissent rejoindre B il faut impérativement que la vitesse d’éloignement entre A et B soit inférieure à ces 100km/h.

et on m'a dit que la conclusion est fausse ( voir pb de la fourmi) je trouve ça vraiment étrange .

Merci mille fois d'avance à celui ou celle qui réussira à me rendre compréhensible cet étrange phénomène.
-----

[Médiat]

Sans faire de calcul, on ne peut pas résoudre ce problème, mais on peut comprendre pourquoi notre intuition ne fonctionne pas : quand on étire l'élastique, on déplace aussi la fourmi.

[pachacamac]

Okay, mais ce résultat est tellement étonnant que je me permet d'insister encore un peu.

Vous ( les mathématiciens) confirmez que le résultat et/ou sa démonstration est correcte ?

Je comprend que la fourmi va profiter de l'expansion de l’élastique mais si on prend les 10 premières secondes, la fourmis va avancer de 10 cm + une toute petite fraction des 10 km d'allongement (que j'ai du mal à déterminer ) alors que le trajet qui reste à faire deviendra 11 km - ( 1 cm + avec la petite expansion pour 1 cm ) donc il semble ( intuitivement) qu'elle aura encore plus de trajet à faire ...

[pm42]

Vu que c'est le résultat le plus contre intuitif que j'ai jamais rencontré en math, je voudrais savoir si quelqu'un(e) pourrait expliquer ce résultat avec des mots et des phrases plutôt qu'avec des équations.

Pas forcément. C'est pour ça qu'on fait des maths justement : pour dépasser notre intuition (entre autres).

Ce n'est pas plus contre-intuitif que https://fr.wikipedia.org/wiki/Paradoxe_de_Banach-Tarski ou pas mal d'autres choses.

[A voir en vidéo sur Futura]

[Médiat]

Oui, la démonstration est correcte, elle repose sur la divergence de la série harmonique. Le déplacement de la fourmi dépend de la position d'icelle sur l'élastique, par exemple si la fourmi est au milieu d'un élastique de 1km (donc à 500m) et qu'on étire cet élastique de 1 km, la fourmi sera toujours au milieu donc à 1lm (plus son déplacement propre)

[pachacamac]

@pm42 : oui mais j'ai dit "que j'ai rencontré" c'est donc personnel et ce rapporte à moi qui n'ait pas fait d'étude supérieure en math. L’énoncé du problème est particulièrement simple et compréhensible par tous et je parierais gros que que plus de 99 % des gens qui non pas étudié les math au niveau supérieur répondrai que la fourmi n'atteindrai jamais le bout de l'élastique.
Après je n'ai aucun doute sur l'utilité des math, que ça peut peut très compliqué, et que cela permet d'aller beaucoup beaucoup plus loin que nous le permet l'intuition et le sens commun (entre autre)

@ Médiat : c'est un peut dommage qu'une erreur typographique c'est glissé dans ton exemple qui rend diffcile sa compréhension
"la fourmi sera toujours au milieu donc à 1lm (plus son déplacement propre)

"si la fourmi est au milieu d'un élastique de 1km (donc à 500m)"

heu... dans notre exemple 1 km c'est la longueur initiale de l’élastique donc quand la fourmi sera au milieu de l’élastique ( je me demande encore comment elle va faire pour y arriver ) l’élastique aura une longueur très supérieure à 1 km...
là il me semble que tu changes les données du problème en remplçant un élastique de 1 km par un élastique de 500 m

Aussi, en n’espérant ne pas abuser, dans l'exemple de la voiture qui roule à 100 km/h et qui doit faire un trajet sur une route élastique de longueur initiale 1000km et qui s' expend de 200 km chaque heure, serait t'il possible de calculer simplement où elle se trouve au bout d'une heure (quand la route aura une longueur de 1200 km)

Merci

[pachacamac]

N.B. @pm42 désolé j'avais mal compris ton message, j'annule donc ma remarque

[jacknicklaus]

Bonjour

Aussi, en n’espérant ne pas abuser, dans l'exemple de la voiture qui roule à 100 km/h et qui doit faire un trajet sur une route élastique de longueur initiale 1000km et qui s' expend de 200 km chaque heure, serait t'il possible de calculer simplement où elle se trouve au bout d'une heure (quand la route aura une longueur de 1200 km)

elle sera au km 109, sauf erreur.
au bout de 10 heures (heure d'arrivée si la route ne s'étend pas) elle sera au km 1648

[Médiat]

Mon exemple était volontairement caricatural (sans compter la typo) pour vous faire comprendre, j'ai échoué !

Si vous voulez faire les calculs :

Au temps 0 l'élastique mesure 1km et la fourmi est à la distance 0.

Une étape = la fourmi avance de 1 cm et ensuite l'élastique s'allonge de 1 km

Etape 1 : la fourmi avance 1 cm (elle est donc à la position 1/100000 de la longueur de l'élastique), l'élastique s'allonge de 1km, et la fourmi est toujours à 1/100000 de sa longueur, soit 2cm
Etape 2 : la fourmi avance de 1 cm soit à 3cm c'est-à-dire 3/200000 de la longueur de l'élastique (qui est supérieur à 1/100000)


A chaque étape, la fourmi va avancer en termes de 1/100000ième de la longueur totale, avec une augmentation qui diminue, certes à chaque fois, mais qui avance inexorablement et finira par dépasser les 100000 1/100000ième, c'est-à-dire par atteindre la fin de l'élastique

[pachacamac]

Okay. Merci j'ai compris.
A l'occasion j' essaierai de faire l'exercice avec la voiture pour voir si j'arrive au même résultat que jacknicklaus

[mach3]

Je propose une reformulation de la résolution de wikipédia qui peut-être éclairera pachacamac.

L'élastique mesure 1km au repos.
On étiquette les points de l'élastique par un paramètre allant de 0 à 1 (quand l'élastique est au repos, indique simplement le nombre de kilomètres depuis son extrémité gauche).
On s'intéresse à la position du point portant l'étiquette en fonction du temps en considérant que le point est et reste en tandis que le point en occupe la position (1 quand t=0, puis 2 quand t=1, etc). On a simplement .

Prenons la différentielle :


On voit que , c'est la variation de x par rapport à t pour n constant, autrement dit la vitesse du point d'étiquette n.

La vitesse de la fourmi par rapport à l'élastique est constante, c'est à dire que sa vitesse par rapport au point d'étiquette auquel elle se trouve est toujours v.
La vitesse de la fourmi par rapport à l'extrémité gauche de l'élastique, n=0, considérée immobile, est la somme de cette vitesse v avec la vitesse du point d'étiquette (qui vaut justement d'après ce qui précède) où elle se trouve :

En utilisant la différentielle ci-dessus, il vient :



Ce qui nous conduit à

Que l'on peut intégrer :
(la constante d'intégration est nulle car en t=0, la fourmi est en n=0)
On constate que est une fonction strictement croissante du temps et surtout qu'elle tend vers l'infini quand le temps tend vers l'infini. La fourmi peut donc atteindre le point d'étiquette n=1 au bout d'un temps fini.

Il faut bien comprendre que ce résultat est valable pour une croissance linéaire de l'élastique. Peu importe le type de croissance de l'élastique, on aboutira à une fonction strictement croissante (on ne peut pas empêcher la fourmi d'avancer sur l'élastique), mais pas forcément à une fonction qui tend vers l'infini. Si pour une certaine croissance la fonction obtenue tend vers une valeur finie inférieure à 1, la fourmi ne peut pas atteindre le bout de l'élastique. Il semblerait par exemple que si l'élastique au lieu de croitre linéairement, double de longueur régulièrement, n puisse plafonner en dessous de 1 si la vitesse de la fourmi par rapport à l'élastique n'est pas assez élevée (mais il est trop tard pour que je publie ce calcul, il y a surement des erreurs dedans...).

m@ch3

[pm42]

N.B. @pm42 désolé j'avais mal compris ton message, j'annule donc ma remarque

Pas de problème. Ce que je voulais te dire, c'est que ce n'est pas intuitif non plus pour un mathématicien.
Dans certains cas, on a une intuition d'une réponse à une question et on cherche à la démontrer. Là, il y a 4 cas :
- on y arrive rapidement, tout le monde est content
- en cherchant à le montrer, on prouve que c'est faux
- on n'y arrive pas ou alors l'humanité met longtemps. Exemple, le théorème des 4 couleurs, très facile à comprendre, l'enfer à démontrer
- on arrive à montrer que c'est indécidable en fait

Dans les 3 derniers cas, l'intuition a failli. Ce n'est pas grave, elle sert juste à partir dans une direction mais on ne sait pas ce qu'on va y trouver.

Il y a aussi plein de cas où on tombe sur des problèmes et où l'intuition ne dit absolument rien. Feynman raconte ça quand il s'agissait de trouver comment intégrer des fonctions : lui (et ses collègues du projet Manhattan) n'ont pas l'intuition de la bonne méthode tout de suite, c'est plutôt le contraire.
Ils essaient différentes méthodes les unes après les autres jusqu'à en trouver une qui fonctionne.

P.S : Feynman était tellement conscient de ça qu'il s'en servait pour donner aux autres l'impression qu'il avait de super-intuition. Quand ils bloquaient, il éliminait les méthodes les plus courantes vu qu'il savait qu'ils les avaient déjà essayé et allait en chercher des originales et souvent ça marchait. Et un jour où lui même bloquait, Fermi (de mémoire) lui a fait exactement le même coup.

[pachacamac]

Merci mach3

J'ai pu en m'accrochant et en avançant petit à petit comprendre le calcul jusqu'à " ce qui nous conduit à" :



mais ici si on numérote de 1 à 4 les 4 membres de l'équation, pour passer de 2 à 3 tu remplaces le d(t) par d(t+1) on a le droit de faire ça ?

[pachacamac]

Il semblerait par exemple que si l'élastique au lieu de croitre linéairement, double de longueur régulièrement, n puisse plafonner en dessous de 1 si la vitesse de la fourmi par rapport à l'élastique n'est pas assez élevée

Tryss2 a fait ce calcul pour un élastique de 1 m qui double de taille toutes les secondes sur cet ancien fil (dernier post #17) il arrive effectivement à cette conclusion avec même des exemples numériques.
"La fourmi qui se déplace à 1m/s mettra 1.7s pour atteindre le bout de l’élastique, celle qui se déplace à 0.7m/s mettra 6.7s, tandis qu'une fourmi qui se déplace à 0.6m/s ne l'atteindra jamais."

[pachacamac]

J'annule ma remarque #13

d(t+1) = dt +d(1) = d(t) +0 = d(t)

[gg0]

Ou encore, la dérivée de t+1 par rapport à t étant 1, d(t+1)=1 dt.

[pachacamac]

Heu..merci gg0 mais ta réponse m'embrouille plus qu'elle ne m'éclaire...

la dérivée de t+1 par rapport à t c'est bien d (t+1 ) non ?
si oui d(t+1) est égale à 1 et non pas 1dt me semble t'il....

aussi une autre question, puisque la solution du problème de la fourmi a été démontrée, peut t'on parler du "théorème de la fourmi sur un élastique " ou est ce abusif ?

[Médiat]

C'est largement abusé, au mieux c'est un exemple d'utilisation du théorème bien connu : la série harmonique est strictement croissante et non bornée.

[gg0]

Non, la dérivée de t+1 est 1. d(t+1) est la différentielle de t+1. Ne pas confondre. Et revoir les cours de première.

[pachacamac]

@ggO: okay . ça fait bien longtemps que je ne fais plus de mathématiques, mon sommum c'était quand j'ai passé en 1977 un certificat C4 de biomathématiques dans le cadre d'une maitrise de biochimie, mais c’était des mathématiques allégées par rapport aux vrais études en mathématiques et depuis j'ai énormément oublié.
Aussi j' ai pas osé poser la question dans le calcul de mach 3 pourquoi



si on sort le d de la fraction comme il l'a fait il reste dans celle -ci t+1/t+1 =1

@Médiat : Okay. sans sans le dire à personne je vais quand même pour m'en souvenir l’appeler le théorème de la fourmi sur l'élastique, parce que je risque d'oublier le théorème de la série harmonique. Je pense que lorsque je serai très vieux, si j'arrive à ne me souvenir que de deux théorèmes il y aura le pseudo théorème de la fourmi sur l'élastique et celui de Pythagore

[gg0]

La différencielle de f(t) est f'(t) dt
La dérivée de ln(t+1) est 1/(t+1), et d(t+1)=dt.

J'ai l'impression que tu lis un calcul très bizarrement écrit !

[ArchoZaure]

Bonjour.

J'ai du mal aussi à voir le rapport entre l'histoire de la fourmi sur l'élastique et l'histoire de l'expansion de l'univers.
Sur wikipedia il est dit

Relation avec l'expansion de l'Univers
Compte tenu de l'expansion de l'Univers, on peut penser que la lumière de galaxies suffisamment lointaines pourrait ne jamais nous atteindre, particulièrement la lumière de celles qui s'éloignent de nous à une vitesse supérieure à celle de la lumière. Si l'expansion est uniforme, c'est-à-dire que chaque galaxie s'éloigne de nous à une vitesse proportionnelle à sa distance actuelle (et que cette vitesse ne change pas), on est dans la situation exacte du puzzle, ce qui montre que la lumière finira toujours par nous être visible. Cependant, dans l'état actuel de nos connaissances, l'expansion semble accélérer, et la logique du problème ne s'applique plus.

https://fr.wikipedia.org/wiki/Probl%...%C3%A9lastique

Or juste avant pour le problème de la fourmi sur l'élastique il est dit

Une fourmi (le point rouge) marchant sur l'élastique à la vitesse constante de 1 cm/s. L'élastique mesure initialement 4 cm et est étiré à vitesse constante de 2 cm/s.

Si je ne me trompe pas ces deux situations ne sont pas identiques.

1). Pour l'univers on a une expansion qui dépend de la distance et du temps : On ajoute une distance (qui n'est pas constante) qui dépend de la distance actuelle (multipliée par une constante) et ce par unité de temps.
Si on voit ça sous la forme d'une suite on a :
distance(t+1)=distance(t) + distance(t)*cst= distance(t)*(1+cst)

2). Pour l'élastique on a une expansion qui ne dépend pas de la distance mais juste du temps : On ajoute une distance (qui est constante) et ce par unité de temps.
distance(t+1)=distance(t) + cst

On a donc une suite géométrique pour 1). et une suite arithmétique pour 2).
L'analogie proposée par Wikipédia concernant la fourmi sur l'élastique et l'expansion de l'univers est-elle donc fausse ?

[pachacamac]

Bonjour,
Sur un autre post ( en lien sur le post#1) d'astrophysique où l'on discute de la vitesse de récession des galaxie quelqu'un ( Lansberg) pense aussi que cette analogie est fausse.

"je peux me tromper, mais le problème de la fourmi n'est pas l'analogue du problème de la propagation de la lumière dans un univers en expansion. En regardant vite fait la solution proposée sur wiki, on voit une résolution graphique du problème dans laquelle l'élastique s'allonge tout simplement de 2 cm chaque seconde (il passe de 4 à 6, 8 puis 10 cm....).
Ce n'est pas équivalent à l'élastique s'allonge avec un taux de 0,5 cm/s/cm. Au bout de la première seconde l'élastique mesure bien 6cm mais ça diverge après."

[pachacamac]

@jacknicklaus

pachacamac : dans l'exemple de la voiture qui roule à 100 km/h et qui doit faire un trajet sur une route élastique de longueur initiale 1000km et qui s' expand de 200 km chaque heure, serait t'il possible de calculer simplement où elle se trouve au bout d'une heure (quand la route aura une longueur de 1200 km)

jacknicklaus : elle sera au km 109, sauf erreur.,au bout de 10 heures (heure d'arrivée si la route ne s'étend pas) elle sera au km 1648

Serait t' il possible que tu me donnes le détail de ton calcul pour les deux premières secondes ?

Merci

[pachacamac]

rectification : Je voulais dire au bout des deux premières heures

[jacknicklaus]

y'a ka demander



quant à la formule, elle est donnée explicitement dans l'article wikipédia déjà cité https://fr.wikipedia.org/wiki/Probl%...%C3%A9lastique

[pachacamac]

Super! merci beaucoup.

Je pense que j'en ai terminé avec ce problème de la fourmi sur l’élastique et des voitures qui roulent sur des routes qui s'allongent linéairement ou exponentiellement. Sur un autre post d'astrophysique il y des exemples détaillés pour faire ces calculs et j'en ai retenu que si je veux entièrement les comprendre, il ne me reste plus qu'à faire de sérieuses révisions sur les bases élémentaires de certains calculs en math.

Encore merci à tous ceux qui ont participé à ce fils.

Bien cordialement
Gérard
.

[pachacamac]

@gg0

Bonjour

je suis en train de suivre votre conseil et de revoir les bases concernant les équations différentielles

si le " Et revoir les cours de première." concernait celles-ci, comme j'ai cru comprendre, j'ai pas souvenir ( mais ça fait longtemps) qu'elle était au programme.

En prenant une équation différentielle linéaire homogène des plus simple : ay' +by = 0 pour la résoudre c'est déjà pas simple,

dif2.jpg



Bon dans ce que je lu sur wikipedia les a, b, c sont des fonctions alors qu'au lycée je suppose qu'on travaille avec a, b , c comme des constantes.

si le second membre n'est pas nul ay' + by = c ça se complique encore et sa renvoie à la méthode de Lagrange voir au théorème de Liouville...

[pachacamac]

Pour terminer, et pour les pas trop fort en math voici la formule pour le problème de la voiture ( qu'on m'a montré ) pour calculer le temps d'arrivé au bout de la route qui montre qu'il faut deja un certain niveau en math pour trouver la solution.

[gg0]

Pachacamac, tu confonds la notion de différentielle (dx, dt) avec celle d'équation différentielle. La différentielle de u (la variable étant x) est le produit de la dérivée de u (fonction de x) par rapport à x et de dx (différentielle de u quand u=x) du = u' dx. C'est une notation qui a des interprétations dangereuses très utilisées par certains "non mathématiciens", en particulier en physique, par remplacement d'une petite variation par dx. (*)
Si je te renvoyais aux cours de première, c'est qu'on y étudie la notion de dérivée, à bien connaître avant de parler de différentielle.

Cordialement.

(*) les dx sont apparus historiquement comme des "infiniment petits", notion un peu contradictoire abandonnée par les mathématiciens sous cette forme. D'où la notation de la dérivée de y par rapport à x sous la forme