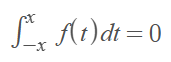montrer que f est impaire
Discussions similaires
-
Par invitec51a08af dans le forum Mathématiques du collège et du lycée
Réponses: 18
Dernier message: 26/02/2015, 09h01
-
Par invitefba37ac6 dans le forum Mathématiques du collège et du lycée
Réponses: 10
Dernier message: 15/10/2014, 19h13
-
Par invitee307e68c dans le forum Mathématiques du supérieur
Réponses: 17
Dernier message: 02/10/2011, 20h15
-
Par invited142144b dans le forum Mathématiques du supérieur
Réponses: 9
Dernier message: 26/09/2010, 14h44
-
Par invitee0ecf794 dans le forum Mathématiques du collège et du lycée
Réponses: 15
Dernier message: 24/04/2007, 16h39



 ?
?