Fusée à eau, énergie stockée par compression et quantité d'eau idéale

[lucas.gautheron]

Bonjour à tous,

Je cherche à déterminer la quantité optimale d'eau à insérer dans une fusée à eau pour que celle-ci aille le plus loin possible. (http://fr.wikipedia.org/wiki/Fus%C3%A9e_%C3%A0_eau)
L'idée est donc de trouver les quantités idéales d'air et d'eau à introduire dans la fusée (qui est une bouteille).
J'ai posé le problème de cette façon :
L'eau est la masse éjectée qui par conservation de la quantité de mouvement, propulse la fusée.
L'air comprimé est la source d'énergie du système.
S'il n'y a pas assez d'eau, il n'y a pas suffisamment de masse à éjecter (donc pas assez de quantité de mouvement échangée) et la propulsion n'est plus maximale
S'il y a trop d'eau en volume dans la bouteille, il y a moins d'air, donc moins d'énergie disponible.
(On néglige les effets de propulsions dus à l'air).

On considère le système libre (pas de gravité), parce que corrigez moi si je me trompe, ça ne changera pas les résultats de l'étude.
L'énergie mécanique se conserve :

A l'état initiale l'énergie est sous forme potentielle uniquement, due à la compression de l'air.
Ma première question est donc : comment déterminer l'énergie potentielle disponible ? J'ai fait quelques recherches, cela dépend apparemment beaucoup du processus de compression (dans notre cas elle se fait à la pompe à vélo)
Pour ne pas rester bloquer, j'ai posé avec :
P = pression
V_a = Volume d'air
V = Volume de la bouteille
V_e = Volume d'eau inséré

L'énergie cinétique est la somme de l'énergie cinétique due à la fusée de masse M à vide et de vitesse v à l'état final + l'énergie cinétique de l'eau éjectée à l'état final toujours (masse , vitesse d'éjection notée u)
D'où (est-ce bien correct ?)

D'où (1)

Il reste à exprimer en fonction de v, et c'est possible, l'étude est faite dans la manuel de LPFR et qu'il me corrige si je me trompe, on peut appliquer ici son résultat, càd :


Mais et on a :



En remplaçant dans (1) on obtient :


Cette expression est un peu compliqué et plutôt que de résoudre , je l'ai calculé avec des valeurs réalistes de M, P, V, etc.
Dans le cas suivant :
M = 0.1 kg
P = 10 bar
V = 1 L

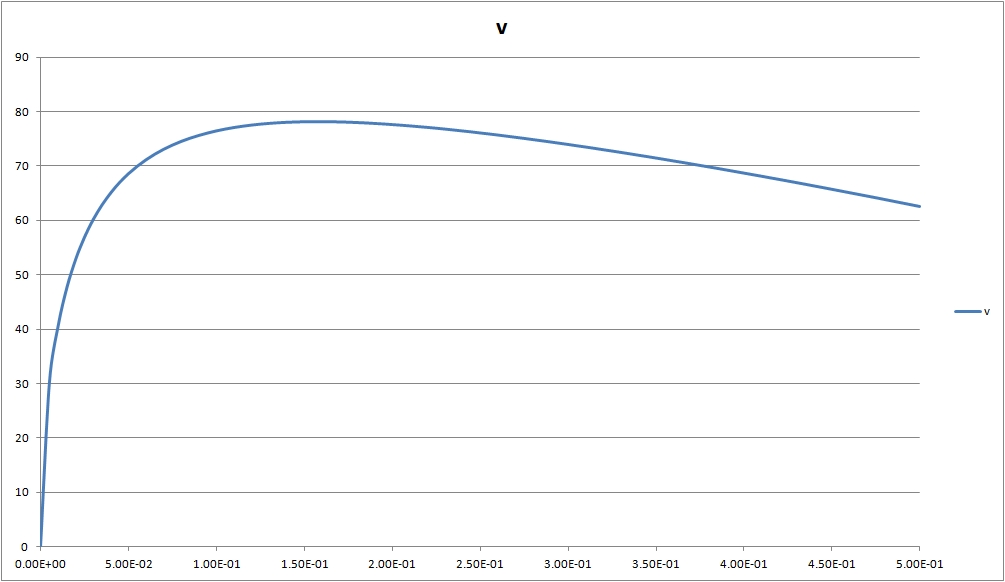
Je trouve cette courbe au final :
XXXXXXXXXX



La vitesse (v) est en ordonnée (en m/s)
Le volume d'eau est en abscisse (en L)

L'étude donne donc un extremum à 15 cL environ dans ces conditions. Le problème, c'est qu'empiriquement, nous avons déterminé que ce volume idéal était de 1/3 de celui de la bouteille, donc un peu plus de 30 cL.
Les valeurs de vitesse sont élevées, mais on ne cherche pas à les déterminer avec exactitude. Encore une fois, on souhaite résoudre , et tant que les approximations ne changent pas de façon significative la solution de cette équation, alors ça n'a aucune importance.

D'où ma deuxième question : où sont mes erreurs ?

Merci d'avance et désolé pour ce post un peu long.
Et n'hésitez pas à me le dire si je suis complètement à côté de la plaque. Il était tard quand j'ai fait ça hier soir


A+,
-----

[LPFR]

Bonjour.
La quantité de mouvement n'est conservée qu'en absence de forces extérieures. Ici vous avez le poids de la bouteille (avec l'eau) qui al pousse vers le bas.
md²h/dt² = F - mg
Ce qui faut utiliser de F dt = dm v, ou 'v' est la vitesse d'éjection de l'eau.
Cela vous donne F = v(dm/dt)
Pour calculer 'v' et dm/dt, il faut faire la supposition que la perte d'énergie du gaz P.dV est égale à l'énergie cinétique donnée à l'eau en sortie P.dV = ½ (rhô. dV) v².

Finalement, le processus de décompression de l'air dans la bouteille est adiabatique. Donc:

Au revoir.

[invite07941352]

Bonjour,
Cela fait très longtemps que je me pose ce problème sans savoir le résoudre ( en jouant avec mes petits enfants ...).
Tout ce que je souhaite, c'est que, à la fin de votre discussion , il y ait une possibilité de trouver simplement la quantité d'eau en fonction de la pression d'air , disons pour la bouteille couramment utilisée, celle de 1.5 L .
Je trouve par exemple, votre valeur choisie de 10 bars trop élevée . Dans mes essais , je gonfle avec une pompe à pied auto et le système se désolidarise à moins de 2 bars , me semble t il . Mais cela , je pourrais le mesurer avec précision . Mais faire le calcul, non ...

[lucas.gautheron]

Bonjour !
Merci beaucoup pour votre réponse.
Je suis d'accord, en réalité le poids agit et la quantité de mouvement n'est pas conservé. Je pensais que cela n'aurait pas d'incidence sur le résultat final cependant. Je vais bien sur faire ce que vous dites quand même
Par rapport au reste, je vois où vous voulez en venir. Nous sommes d'accord pour dire que v est la vitesse d'éjection de l'eau vue par la fusée, et pas dans le système du centre de masse n'est-ce pas ?
Pour l'indice adiabatique, je dois bien prendre n'est-ce pas ?

Merci encore ! Je vous tiens au courant.

A+,

[A voir en vidéo sur Futura]

[lucas.gautheron]

Bonjour catmandou,

Bonjour,
Cela fait très longtemps que je me pose ce problème sans savoir le résoudre ( en jouant avec mes petits enfants ...).
Tout ce que je souhaite, c'est que, à la fin de votre discussion , il y ait une possibilité de trouver simplement la quantité d'eau en fonction de la pression d'air , disons pour la bouteille couramment utilisée, celle de 1.5 L .
Je trouve par exemple, votre valeur choisie de 10 bars trop élevée . Dans mes essais , je gonfle avec une pompe à pied auto et le système se désolidarise à moins de 2 bars , me semble t il . Mais cela , je pourrais le mesurer avec précision . Mais faire le calcul, non ...

Pourtant je peux vous assurer que la valeur atteinte est bien d'environ 10 bars !
Comment votre système est-il maintenu ?
Dans notre cas il y a différentes sortes de maintien, un système utilisant des pinces - en gros-, et un autre un peu plus sophistiqué () utilisant un bouchon et un vérin : http://ppe.sciencestechniques.fr/compression.html

A+,

[Amanuensis]

Pour le calcul, l'énergie cinétique de l'eau éjectée ne peut pas être en mu²/2. L'énergie étant calculée dans le référentiel sol, la vitesse sol d'une masse dm d'eau éjectée à la vitesse u(t) quand la bouteille va à v(t) est 1/2 (v-u)² dm, si du moins la vitesse d'éjection u est bien celle relative à la bouteille.

[Amanuensis]

Une autre approche du calcul s'inspire de celui aboutissant à l'équation de Tsiolkowski (cf. http://fr.wikipedia.org/wiki/%C3%89q...de_Tsiolkovski), en prenant en compte une vitesse d'éjection variable.

Si on prend d'abord le cas hors pesanteur on a par conservation de la quantité de mouvement mdv = u(m)dm, avec m la masse (variable), v la vitesse sol, u la vitesse relative d'éjection (supposée ne dépendre que de m).

D'où une vitesse finale obtenue par intégration de u(m)dm/m entre la masse initiale (eau + bouteille) et la masse finale (bouteille seule).

La pesanteur soustrait gT, T la durée de la phase de propulsion, obtenue à partir du débit d'eau q(m) qu'on peut supposer ne dépendre que de m, par intégration de dt = dm/q(m)

On a donc besoin de deux formules venant de l'hydrodynamisme, la vitesse d'éjection en fonction de la pression, et le débit d'éjection en fonction de la pression. Et de la formule donnant la pression en fonction de m, venant de la thermodynamique.

[invite07941352]

Bonjour catmandou,


Pourtant je peux vous assurer que la valeur atteinte est bien d'environ 10 bars !
Comment votre système est-il maintenu ?
Dans notre cas il y a différentes sortes de maintien, un système utilisant des pinces - en gros-, et un autre un peu plus sophistiqué () utilisant un bouchon et un vérin : http://ppe.sciencestechniques.fr/compression.html

A+,

La mienne, c'est le premier prix du système du commerce : on doit faire soi-même le corps de la fusée à l'aide de 2 bouteilles PET emboîtées et scotchées, et l'embout de gonflage tient juste par l' élasticité d'une pièce caoutchouc qui sert de tuyère et porte les 3 ailettes de guidage . De plus ma pompe à pied possède un petit mano 7 bars et je n'atteins jamais cette valeur .Et pourtant, même vers 2, au mieux 3 bars , la fusée s'élève bien mais je ne sais pas évaluer la hauteur . D'où ma demande de vos résultats à partir de 2 bars, si possible . Merci .

[lucas.gautheron]

Bonjour Amanuensis,

Pour le calcul, l'énergie cinétique de l'eau éjectée ne peut pas être en mu²/2. L'énergie étant calculée dans le référentiel sol, la vitesse sol d'une masse dm d'eau éjectée à la vitesse u(t) quand la bouteille va à v(t) est 1/2 (v-u)² dm, si du moins la vitesse d'éjection u est bien celle relative à la bouteille.

D'où la question que j'ai posée à LPFR. Mais si on se place par rapport au sol, alors l'énergie cinétique de la fusée n'est pas nulle, et c'est plus compliqué (c'est l'étude que j'ai faite, sans gravité)
D'après le post de LPFR, il me semble que v est la vitesse d'éjection vue par la fusée.

Une autre approche du calcul s'inspire de celui aboutissant à l'équation de Tsiolkowski (cf. http://fr.wikipedia.org/wiki/%C3%89q...de_Tsiolkovski), en prenant en compte une vitesse d'éjection variable.

Si on prend d'abord le cas hors pesanteur on a par conservation de la quantité de mouvement mdv = u(m)dm, avec m la masse (variable), v la vitesse sol, u la vitesse relative d'éjection (supposée ne dépendre que de m).

D'où une vitesse finale obtenue par intégration de u(m)dm/m entre la masse initiale (eau + bouteille) et la masse finale (bouteille seule).

La pesanteur soustrait gT, T la durée de la phase de propulsion, obtenue à partir du débit d'eau q(m) qu'on peut supposer ne dépendre que de m, par intégration de dt = dm/q(m)

On a donc besoin de deux formules venant de l'hydrodynamisme, la vitesse d'éjection en fonction de la pression, et le débit d'éjection en fonction de la pression. Et de la formule donnant la pression en fonction de m, venant de la thermodynamique.

Ce que vous dites dans un premier temps ressemble vraiment à ce que j'ai fait. D'ailleurs l'équation de Tsiolkovski est celle que j'ai utilisée dans mon premier post. Vous confirmez que ma première étude est valide sans pesanteur donc ? (à l'exception de l'énergie E).
Parce qu'il ne s'agit nécessairement de déterminer la hauteur maximale atteinte sur un tir vertical, mais seulement le volme V_e optimal. Il me semblait que le résultat ne serait pas différent sans gravité. Apparemment non, donc je vais modifier mon étude en prenant compte de vos remarques.
Je vous tiendrai au courant de l'avancement, mais j'ai un doute suite à la remarque que vous avez faite dans votre premier post.


Merci.
A+,

[lucas.gautheron]

La mienne, c'est le premier prix du système du commerce : on doit faire soi-même le corps de la fusée à l'aide de 2 bouteilles PET emboîtées et scotchées, et l'embout de gonflage tient juste par l' élasticité d'une pièce caoutchouc qui sert de tuyère et porte les 3 ailettes de guidage . De plus ma pompe à pied possède un petit mano 7 bars et je n'atteins jamais cette valeur .Et pourtant, même vers 2, au mieux 3 bars , la fusée s'élève bien mais je ne sais pas évaluer la hauteur . D'où ma demande de vos résultats à partir de 2 bars, si possible . Merci .

Qu'entendez vous par "vos résultats" ? Si vous parlez par exemple de la portée d'un tir observée en effectuant un lancer à deux bars, je ne peux pas vous répondre (pas essayé)
Si vous parlez de mes calculs et du volume idéal d'eau que je trouve dans le cas que vous précisez, alors je trouve 20 cL environ (2 bars, bouteille d'1.5L, masse de 0.1kg)
Là encore, je trouve ça faible. (mais l'ordre de grandeur est bon )

A+,

[Amanuensis]

mais j'ai un doute suite à la remarque que vous avez faite dans votre premier post.

La remarque ne s'appliquait qu'au calcul à partir de l'énergie. La dérivation selon la méthode pour l'équation de Tsiolkovski ne passe pas par l'énergie. (Et du coup je ne la vois pas dans le message #1, qui apparaît comme un calcul basé sur la conservation de l'énergie.)

Dans la seconde dérivation le udm est bien avec u la vitesse relative, la masse avait avant éjection une quantité de mouvement vdm et après éjection (v-u) dm, d'où une différence de udm (au signe près).

[Amanuensis]

Parce qu'il ne s'agit nécessairement de déterminer la hauteur maximale atteinte sur un tir vertical, mais seulement le volme V_e optimal. Il me semblait que le résultat ne serait pas différent sans gravité. Apparemment non, donc je vais modifier mon étude en prenant compte de vos remarques.

C'est facile de voir que la pesanteur intervient : si la poussée ne dépasse jamais le poids, la bouteille ne décollera pas et la vitesse finale sera nulle ! Alors que hors pesanteur cela donnerait une vitesse non nulle.

L'effet de la pesanteur va intervenir via q(m), qui n'a pas de relation simple avec u(m). Suffit d'imaginer une fusée avec un tout petit trou d'éjection : la vitesse u(m) n'est pas beaucoup affectée par la taille du trou (dans une certaine plage), mais q(m) si ! Avec un trou très petit la fusée ne décolle pas, alors que la poussée est la même au total (si l'hypothèse u(m) indépendante de la taille du trou tient).

On peut penser que l'optimisation hors pesanteur est indépendante de la taille du trou d'éjection (si pas trop grand), alors que l'optimisation avec pesanteur dépend de la taille du trou. Ou, si cette taille est variable, j'imagine qu'il faille prendre la plus grand possible telle que la vitesse d'éjection ne soit pas significativement affectée par une taille trop grande. (De façon à minimiser le temps de la phase de propulsion.)

[lucas.gautheron]

C'est facile de voir que la pesanteur intervient : si la poussée ne dépasse jamais le poids, la bouteille ne décollera pas et la vitesse finale sera nulle ! Alors que hors pesanteur cela donnerait une vitesse non nulle.

Bien sûr. Seulement, on peut se dire que ce qui est le plus efficace hors gravité est aussi le plus efficace sur Terre. Après selon l'intensité de la pesanteur et les autres données peut être qu'il n'y aura pas de propulsion. Mais il y a un cas optimal, et je pensais qu'il était le même partout.

L'effet de la pesanteur va intervenir via q(m), qui n'a pas de relation simple avec u(m). Suffit d'imaginer une fusée avec un tout petit trou d'éjection : la vitesse u(m) n'est pas beaucoup affectée par la taille du trou (dans une certaine plage), mais q(m) si ! Avec un trou très petit la fusée ne décolle pas, alors que la poussée est la même au total (si l'hypothèse u(m) indépendante de la taille du trou tient).

On peut penser que l'optimisation hors pesanteur est indépendante de la taille du trou d'éjection (si pas trop grand), alors que l'optimisation avec pesanteur dépend de la taille du trou. Ou, si cette taille est variable, j'imagine qu'il faille prendre la plus grand possible telle que la vitesse d'éjection ne soit pas significativement affectée par une taille trop grande. (De façon à minimiser le temps de la phase de propulsion.)

OK. c'est cet aspect que je n'avais pas saisi.
Merci.
PS : pour le calcul sans pesanteur, en corrigeant l'erreur dont vous faites mention, le point optimum n'est pas déplacé j'ai l'impression.

Merci encore.

A+,

[invite07941352]

C'est bien du résultat de vos calculs dont je voulais parler . Et donc avez vous maintenant une formulation facilement applicable qui permette de trouver le volume d'eau en fonction du volume du réservoir et de la pression de l'air ? Même peut être une formulation approchée mais "pratique" ?

[calculair]

Bonjour,

Je pense en effet qu'il faut tenir compte de la gravité , mais aussi de la resistance de l'air

en tentant de mettre en equation. La variation de vitesse de la fusée dans l'espace et hors gravité est

dV = Ve dm /m

dV/dt = Ve dm/( m dt)

mdV/dt = ve dm/dt

en introduisant la gravité et la resistance de l'air

m dV/dt - mg -1/2 Cx S V² = Ve dm/dt

En supposant la perte de masse lineaire durant le temps de propulsion perte de masse = a t

dm = a

l'eequation devient

at dV/dt = at g - 1/2 Cx S V² = Ve a


Reste à integrer cette equation durant la phase de propulsion, puis dans la phase balistique ou a = 0

Qu"en pensez vous ?

[calculair]

bonjour

il serait plus juste de dire que la masse dela fusée est M(t) = Mf - at


(Mf -at)dV/dt - (Mf -at) Cx S V² = Ve a

[LPFR]

Bonjour !
Merci beaucoup pour votre réponse.
Je suis d'accord, en réalité le poids agit et la quantité de mouvement n'est pas conservé. Je pensais que cela n'aurait pas d'incidence sur le résultat final cependant. Je vais bien sur faire ce que vous dites quand même
Par rapport au reste, je vois où vous voulez en venir. Nous sommes d'accord pour dire que v est la vitesse d'éjection de l'eau vue par la fusée, et pas dans le système du centre de masse n'est-ce pas ?
Pour l'indice adiabatique, je dois bien prendre n'est-ce pas ?

Merci encore ! Je vous tiens au courant.

A+,

Re.
Oui. Nous sommes d'accord.
On trouve un tas de pages (surtout en anglais) sur les mécanismes de fixation/ libération des bouteilles.
Et des informations intéressantes dans wikipedia.
A+

[Amanuensis]

PS : pour le calcul sans pesanteur, en corrigeant l'erreur dont vous faites mention, le point optimum n'est pas déplacé j'ai l'impression.

J'ai la même impression, au sens ci-après :

Si l'approximation consistant à dire que le débit q(m) ne dépend que de la taille du trou, et que u(m) au contraire n'en dépend pas, cela "sépare les variables". Le point optimum en terme de volume d'eau et de pression est le même avec ou sans pesanteur. L'optimisation dans le cas avec pesanteur consiste à optimiser la taille du trou, en plus et séparément

[lucas.gautheron]

Bonjour,

[...]

Qu"en pensez vous ?

Bonsoir calculair,
Merci à vous. J'en pense que j'ai maintenant le choix parmi pas mal de méthodes !
Cependant, dans un premier temps, si ce n'est pas nécessaire, je ne pense pas prendre en compte la trainée.

Re.
Oui. Nous sommes d'accord.
On trouve un tas de pages (surtout en anglais) sur les mécanismes de fixation/ libération des bouteilles.
Et des informations intéressantes dans wikipedia.
A+

Merci !
Un ami m'avait donné un lien vers un site très sympa (en anglais également) mais je n'ai pas trop regardé
de même pour la page wiki en anglais

J'ai la même impression, au sens ci-après :

Si l'approximation consistant à dire que le débit q(m) ne dépend que de la taille du trou, et que u(m) au contraire n'en dépend pas, cela "sépare les variables". Le point optimum en terme de volume d'eau et de pression est le même avec ou sans pesanteur. L'optimisation dans le cas avec pesanteur consiste à optimiser la taille du trou, en plus et séparément

OK. Je vais donc prendre en compte toutes vos considérations mais je vais procéder par étapes, en étudiant le système du cas le plus simple au cas le plus compliqué.

Merci à tous, et bonne soirée !

PS : @catmandou : pour l'instant je n'ai pas de résultat vraiment satisfaisant. Je vais corriger mes erreurs, tenir compte des remarques apportées ici, puis je vous tiendrai au courant de mes résultats une fois confrontés à l'expérience j'espère (je demanderai à l'ami sus-cité de refaire quelques essais )

[LPFR]

Bonjour.
Je vous donne un lien intéressant sur les calculs:
http://www.sciencebits.com/RocketCalculator
lequel donne un lien vers un calculateur:
http://www.sciencebits.com/RocketCal...r?fromForm=yes
Au revoir.

[Amanuensis]

Cause déterrage d'une vieille discussion, je suis tombé là-dessus : http://forums.futura-sciences.com/as...ml#post3496716

Le fichier attaché au message est peut-être pertinent.

[lucas.gautheron]

Bonjour,

Merci à tous, ces liens contiennent des informations très complètes, qui devraient me suffire largement !
Je regarde tout ça de près.

A+,

[lucas.gautheron]

Au passage, pour calculer le libéré, ce que je n'avais pas su faire, j'ai essayé cette méthode hier soir :



et d'où :



Comme primitive je trouve :
D'où
Ce raisonnement est-il correct ? j'ai de gros doutes

Merci

PS : je termine de regarder vos liens, j'essaierai de mettre un formulaire de calcul en ligne pour trouver le volume idéal en fonction des caractéristiques de la fusée et des paramètres de lancement.

A+,

[LPFR]

Re.
Oui, le calcul me semble correct.
A+

[lucas.gautheron]

Re et merci pour la vérification ! Pour les bornes êtes vous d'accord avec ceci ? :
avec P_f = 1 atm (et )

A+,

[LPFR]

Re.
Ça dépend de ce que vous voulez calculer.
(D'ailleurs je me demande quel est l'objet de votre calcul).
Si vois dites que la pression finale est la pression atmosphérique, n'oubliez pas que ça fait un moment que la bouteille a larguée toute son eau.
Et elle a largué toute son eau quand Vf est égal au volume de la bouteille (et la pression loin de la pression atmosphérique).
A+

[lucas.gautheron]

Re.
Ça dépend de ce que vous voulez calculer.
(D'ailleurs je me demande quel est l'objet de votre calcul).
Si vois dites que la pression finale est la pression atmosphérique, n'oubliez pas que ça fait un moment que la bouteille a larguée toute son eau.
Et elle a largué toute son eau quand Vf est égal au volume de la bouteille (et la pression loin de la pression atmosphérique).
A+

Bonsoir,
C'est vrai ce n'est pas très pertinent de borner avec le volume atteint lorsque la pression est la pression atmosphérique.
Je prendrai donc simplement V.
L'intérêt de ce calcul est simplement de calculer l'énergie libérée "utile" par le processus de décompression.

Merci encore.
A+

[calculair]

bonjour,

je ne suis pas sur, mais l'energie liberée par le processus de decompression adiabatique = l'energie de compression dans des conditions adiabatiques.

Dans la phase de propulsion, il y a la phase ou la pression ejecte l'eau, puis la phase finale ou c'est l'air comprimé qui sort par la tuyère. a priori cette derniere phase ne devrait pas apporter un gain significatif à l'engin ( mais rien d'evident car a ce moment là l'engin à une masse reduite ).

J'ai lu que pour ce type de fusée l'optimun serait 1/3 d'eau et 2/3 de gaz, mais j'imagine que cela depend aussi de la pression initiale possible.

le role de la resistance de l'air me parait non negligeable, vitesse elevée et masse faible en fin de propulsion, donc l'energie absorbée par la resistance de l'air peut avoir un effet sur l'altitude atteinte.

[lucas.gautheron]

Bonjour,

bonjour,

je ne suis pas sur, mais l'energie liberée par le processus de decompression adiabatique = l'energie de compression dans des conditions adiabatiques.

Dans la phase de propulsion, il y a la phase ou la pression ejecte l'eau, puis la phase finale ou c'est l'air comprimé qui sort par la tuyère. a priori cette derniere phase ne devrait pas apporter un gain significatif à l'engin ( mais rien d'evident car a ce moment là l'engin à une masse reduite ).

J'ai lu que pour ce type de fusée l'optimun serait 1/3 d'eau et 2/3 de gaz, mais j'imagine que cela depend aussi de la pression initiale possible.

le role de la resistance de l'air me parait non negligeable, vitesse elevée et masse faible en fin de propulsion, donc l'energie absorbée par la resistance de l'air peut avoir un effet sur l'altitude atteinte.

En effet, mais le but n'est pas de connaitre l'altitude atteinte, seulement le volume d'eau optimal. Donc, pour moi, celui qui confère le plus d'énergie cinétique à la fusée. On peut supposer que les frottements ne déplacent pas cet optimum. Non ?


A+,

[calculair]

Bonjour,

En effet a première vue l'energie cinetique max est atteinte en fin de phase de propulsion. Plus precisement la vitesse Max est atteinte peut être en fin de phase de propulsion Eau, ou en fin de propulsion de vidange Air.... Ce n'est pas evident pour moi

Dans l'energie cinetique de la fusée il y a sa masse Ec = 1/2 M V² et M et V sont des variables, ce qui fait qu'en presence de la resistance de l'air et de la gravite eventuellement, cela n'est pas trés clair pour moi de savoir a quel moment du vol l'energie cinetique est maximum.

Exemple, pour une fusée de grande automonie de propulsion avec une poussée modeste, l'engin peut atteindre une vitesse limite stable, V devient constant, M diminue car la fusée ejecte de la masse pour maintenir sa vitesse, alors son energie cinetique diminue.....!!!! C'est un peu tiré par les cheveux, mais je ne sais pas dire, la distance qu'il y a entre cette fusée et celle que tu realises

Les choses ne sont pas simples, certainement à la portée de la NASA, ou d'un bon tableur excel lorsque les equations seront maitrisées!!