Paradoxe des jumeaux et relativité

[invite289c27d7]

Pourriez-vous développer sur un exemple, en particulier la phrase que j'ai soulignée ?

Bonjour,

Je pense que dans ma réponse à Amanuensis répondra à votre question. Si ce n’est pas le cas, dîtes-le moi.

Vous vous mettez sur la ligne de changement de date sur la Terre côté est, et vous sautez côté ouest ("saut instantané"). Et hop, tout le monde change d'âge, a vieilli de 1 jour!

Je ne suis pas d’accord avec cette analogie car dans votre exemple vous ne faîtes effectivement qu’un simple changement d’origine qui change seulement les coordonnées des événements. Si j’appelle Robert un individu situé côté Ouest, votre saut instantané est également instantané pour Robert et l’événement (Robert assis à la terrasse d’un café à 1h de l’après-midi) passant à (Robert assis à la terrasse d’un café à 2 heures de l’après-midi) ne change rien pour Robert. L’événement physique est le même.

Dans le changement de référentiel inertiel R à R’ dont je parle, il y a deux événements différents de la vie de Robert qui entrent en jeu. Vous pourrez ainsi passer de (Robert assis à la terrasse d’un café à 1h de l’après-midi) à (Robert debout à minuit en train d’observer les étoiles au télescope). Du temps a passé pour Robert durant le changement de référentiel. Il a réellement vieilli, il n’a pas seulement avancé sa montre d’une heure.

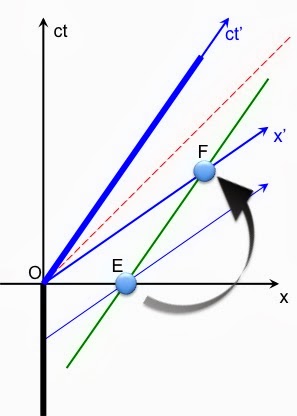
Plus rigoureusement, voici comment je représente un tel saut dans un diagramme de Minkowski.



Le référentiel R est en noir, R’ est en bleu. La ligne d’univers du voyageur est représentée en gras. Le saut se fait à l’origine des deux repères. Robert est immobile dans R’, sa ligne d’univers est la ligne verte. Avant le saut, Robert est en E sur la ligne de simultanéité du sauteur, après le saut, Robert est en F sur la nouvelle ligne de simultanéité.

Remarquons aussi qu'on peut changer "instantanément" de système de coordonnées n'importe quand, cela n'est pas lié à une accélération

Oui, un changement de système de coordonnées n’est pas une accélération. En revanche, sauter dans un train en marche est une accélération. C’est de ce saut dont je parle.

Changer de système de coordonnées au milieu de l'analyse d'un phénomène n'a aucun intérêt (litote), cela crée des discontinuités artificielles entre autres effets, et tout une collection de paradoxes si on perd de vue que la cause des effets est le changement de système de coordonnées.

Oui, mais ce n’est pas ça que je fais.

L’intérêt d’expliciter ce saut est qu’il est à la base de la compréhension du paradoxe des jumeaux. Et comme c’est l’objet du fil…
-----

[PPathfindeRR]

je vois que le sujet continu actuellement et je reste en attente de réponse de l'autre coté...
C'est clair qu'il faut éviter de créer deux sujet identique (paradoxe des jumeaux), c'est embêtant de passer de l'un à l'autre, alors qu'on traite de la même chose !

[Amanuensis]

Oui, mais ce n’est pas ça que je fais.

Dommage que "changer de référentiel" n'est rien d'autre qu'un changement de référence. Et la différence entre référentiel et système de coordonnées n'est pas pertinente sur ce point.

L’intérêt d’expliciter ce saut est qu’il est à la base de la compréhension du paradoxe des jumeaux.

Pour moi c'est à la base d'une des formes d'incompréhension du "paradoxe".

Des explications du paradoxe des jumeaux, il y en a plein dans des discussions plus anciennes et dans la littérature, et pas mal appuyées sur des références à des spécialistes. Je ne vois pas l'intérêt à en rajouter avec des phrases comme "tous les passagers changent d'âge".

L'âge des jumeaux, c'est leur temps propre.
Et le temps propre d'un jumeau n'est pas relatif à un référentiel/observateur: la durée mesurée (et affichée!) par "son" horloge est la même, quel que soit le référentiel/observateur.

Oui. C'est la meilleure manière d'interpréter le terme "âge". Et je ne suis pas sûr qu'une quelconque autre n'entraîne pas une confusion.

[Amanuensis]

Soyons plus précis. Usuellement, le "saut d'âge" est présenté comme une objection, comme une bizarrerie à résoudre, et non comme une "explication".

La résolution de ce "saut d'âge" est usuellement présentée comme un artefact dû à un changement de système de coordonnées. Voir par exemple: http://math.ucr.edu/home/baez/physic.../twin_gap.html

J'en traduit une phrase "The apparent "gap" is just an accounting error, caused by switching from one frame to another.": Le saut apparent est juste une erreur de comptabilité, causée par le basculement d'un référentiel à un autre.

[invite289c27d7]

Dommage que "changer de référentiel" n'est rien d'autre qu'un changement de référence. Et la différence entre référentiel et système de coordonnées n'est pas pertinente sur ce point.

Nous sommes bien évidemment d’accord que :

• Lors d’un changement de référentiel, les événements changent de coordonnées. L’événement E existe toujours dans R’ avec des coordonnées différentes
• Oui, on peut décrire le parcours du jumeau voyageur dans un seul référentiel inertiel sans changer de système de coordonnées.

Ce que je dis simplement c’est que l’axe de simultanéité du jumeau voyageur balaie la ligne d’univers du jumeau sédentaire lors du demi-tour (ou encore que la ligne de simultanéité du référentiel aller ne croise pas la ligne d’univers du jumeau sédentaire au même événement que la ligne de simultanéité du référentiel retour).

Sur le fond, malgré vos critiques sur la manière dont je présente les choses, c'est un fait.

Après vous pouvez ne pas être d’accord avec la manière dont je nomme ce phénomène.

Pour moi c'est à la base d'une des formes d'incompréhension du "paradoxe".

Pour moi la base de l’incompréhension du paradoxe est de comprendre pourquoi la situation n’est pas symétrique puisque chacun voit l’autre vieillir moins vite.

Donc il faut bien expliquer comment « vu » du voyageur, le jumeau sédentaire peut être plus vieux à la fin de l’histoire. Là encore vous pouvez considérer que la question est mal posée et que « voir » ne veut rien dire. Mais c’est comme ça que la question est posée.

Quand le voyageur retrouve son frère plus vieux, la question basique est « quand est-ce qu’il a vieilli plus vite ». Là encore, ce vocabulaire ne vous plait pas mais c’est celui de la question des non spécialistes (dont je suis).

J’essaie de rendre les choses simples en racontant l’histoire en 3 étapes: aller / demi-tour / retour. A chaque étape, le jumeau sédentaire vieillit et le total fait les 20 ans de l’histoire.

Des explications du paradoxe des jumeaux, il y en a plein dans des discussions plus anciennes et dans la littérature, et pas mal appuyées sur des références à des spécialistes. Je ne vois pas l'intérêt à en rajouter avec des phrases comme "tous les passagers changent d'âge".

C’est donc que c’est peut-être pas si clair que ça !

J’imagine que les gens qui s’interrogent sur le paradoxe vont d’abord sur Wikipedia et voilà ce qu’on lit :

« Cette différence fait que la relativité restreinte s'applique différemment à l'un et à l'autre »

Perso, ça m’arrache les yeux de lire que la relativité restreinte s’applique différemment, mais bon…

« Le jumeau mobile observe pendant le trajet aller le jumeau fixe vieillir plus lentement que lui, puis pendant le trajet retour, beaucoup plus rapidement que lui. »

Ce qui est complètement faux.

Donc si au bout d’un siècle, on n’est toujours pas capable d’expliquer clairement le paradoxe, c’est bien qu’il y a un problème de pédagogie.

Alors j’essaie avec la méthode qui m’a permis de comprendre. Peut-être que ça peut en aider d’autres…

L'âge des jumeaux, c'est leur temps propre.
Et le temps propre d'un jumeau n'est pas relatif à un référentiel/observateur: la durée mesurée (et affichée!) par "son" horloge est la même, quel que soit le référentiel/observateur.

Oui. C'est la meilleure manière d'interpréter le terme "âge". Et je ne suis pas sûr qu'une quelconque autre n'entraîne pas une confusion.

C’est comme ça que je l’interprète également (cf message #27 « âge = indication des horloges du référentiel inertiel dans lequel l’observateur est immobile »).

Le vieillissement dont je parle est la différence entre les âges en E et F (cf message #31). Comme ces événements sont sur la ligne d’univers, c’est bien un vieillissement indépendant du référentiel choisi.

[invite289c27d7]

Soyons plus précis. Usuellement, le "saut d'âge" est présenté comme une objection, comme une bizarrerie à résoudre, et non comme une "explication".

Donc, je n'affabule pas en parlant d'un "vieillissement instantané" ou d'un "time gap" (vous avez dû noter que j’avais soigneusement évité de ne pas copier ce passage dans un message précédent lorsque j’ai cité Baez. J’aurais peut-être dû après tout).

"The apparent "gap" is just an accounting error, caused by switching from one frame to another.": Le saut apparent est juste une erreur de comptabilité, causée par le basculement d'un référentiel à un autre.

Vous imaginez bien entendu que je ne suis pas d’accord avec cette interprétation mais au moins on va parler de la même chose à présent car c’est le cœur du débat que j’essaie d’avoir.

En terme de comptabilité, pour moi ça tombe parfaitement :
3,6 + 12,8 + 3,6 = 20
Je ne vois pas d’erreur.

J’ai donc deux questions :

1. C’est quoi une erreur de comptabilité en physique ?
2. C’est quoi la bonne comptabilisation ?

[Amanuensis]

Nous sommes bien évidemment d’accord que :[LIST][*]Lors d’un changement de référentiel, les événements changent de coordonnées. L’événement E existe toujours dans R’ avec des coordonnées différentes

Sur le fond probable (en me basant sur l'expérience de la lecture de nombre d'intervenants...) oui. Sur la forme, les connotations des expressions employées, et donc éventuellement sur les concepts sous-jacents, non. ("Exister dans un référentiel" n'a aucun sens sérieux pour moi, par exemple.)

Ce que je dis simplement c’est que l’axe de simultanéité du jumeau voyageur balaie la ligne d’univers du jumeau sédentaire lors du demi-tour (ou encore que la ligne de simultanéité du référentiel aller ne croise pas la ligne d’univers du jumeau sédentaire au même événement que la ligne de simultanéité du référentiel retour).

Terminologie inadaptée. ("axe de simultanéité", "référentiel aller", etc.)

Sur le fond, malgré vos critiques sur la manière dont je présente les choses, c'est un fait.

La relativité restreinte est un fait. Si vous entendez "fond" comme la RR, il n'y a pas de risque qu'on oppose ce fond. C'est la conceptualisation que je critique, bien plus que la présentation.

Pour moi la base de l’incompréhension du paradoxe est de comprendre pourquoi la situation n’est pas symétrique puisque chacun voit l’autre vieillir moins vite.

Dépend de ce que vous appelez "voir". La confusion est entre "voir" et "calculer", comme l'explique d'ailleurs Baez dans la page citée.

Si vous vous contentez de "voir" (voir par exemple l'horloge de l'autre au télescope), il n'y a aucun besoin de parler de référentiel et encore moins de changement de référentiel.

Quand le voyageur retrouve son frère plus vieux, la question basique est « quand est-ce qu’il a vieilli plus vite ».

La question elle-même sous-tend une erreur de conceptualisation. Il n'y aucune raison logique à poser a priori qu'il y ait un "quand" alors que toute la problématique repose sur la conceptualisation du temps.

J’essaie de rendre les choses simples en racontant l’histoire en 3 étapes: aller / demi-tour / retour. A chaque étape, le jumeau sédentaire vieillit et le total fait les 20 ans de l’histoire.

Et j'essaye d'expliquer, en prenant des références extérieures, que l'explication est conceptuellement à côté. Il n'y a pas d'étape de demi-tour pour le jumeau sédentaire, au sens où le "moment" où se passe ce demi-tour n'est défini que de manière arbitraire pour le jumeau sédentaire(1). Le moins arbitraire est de parler du premier instant possible où il peut être informé du demi-tour. Pour le sédentaire, penser qu'il y a un demi-tour avant ce moment tient de la voyance. Il peut faire un calcul en se basant sur l'affirmation (non vérifiée) que l'autre fera demi-tour, il peut faire le calcul a posteriori, mais tout cela procède d'un arbitraire.

(1) C'est d'ailleurs un excellent argument pour la dissymétrie: le voyageur prend en compte le demi-tour au milieu du voyage, alors que c'est impossible pour le sédentaire.

Il n'y a pas de bonne "explication" d'un paradoxe en RR si on laisse passer dans l'expression ne serait-ce qu'un soupçon de temps absolu. Et c'est un exercice difficile.

J’imagine que les gens qui s’interrogent sur le paradoxe vont d’abord sur Wikipedia et voilà ce qu’on lit :

Vous ne pouvez pas justifier votre explication en disant que celle du Wiki est fausse. J'ai proposé une référence que j'estime sérieuse (et je ne suis pas le seul), les pages de Baez.

Donc si au bout d’un siècle, on n’est toujours pas capable d’expliquer clairement le paradoxe, c’est bien qu’il y a un problème de pédagogie.

Ben oui, depuis un siècle il y des gens qui découvrent la RR et qui viennent expliquer à tout le monde comment ça marche selon eux. Et avec le Web, ils sont de plus en plus visibles, et éclipsent les explications claires et pédagogiques des professionnels, des professeurs de physique par exemple. Vous pensez vraiment que les professeurs en université manquent de pédagogie depuis un siècle?

Alors j’essaie avec la méthode qui m’a permis de comprendre. Peut-être que ça peut en aider d’autres…

Uniquement si votre compréhension est bonne, profonde, assise solidement sur une conceptualisation solide. Mon expérience me laisse penser, sur la base de expressions employées (et que vous pensiez qu'elles aident plutôt qu'elles n'apportent de confusion), que ce n'est peut-être pas le cas.

C’est comme ça que je l’interprète également (cf message #27 « âge = indication des horloges du référentiel inertiel dans lequel l’observateur est immobile »).

Le vieillissement dont je parle est la différence entre les âges en E et F (cf message #31). Comme ces événements sont sur la ligne d’univers, c’est bien un vieillissement indépendant du référentiel choisi.

En quoi est-ce un "saut"? Au mieux, vous êtes en train d'assimiler E et F parce que l'un a la même coordonnée temporelle dans le système R que l'autre dans le système R'. L'égalité de coordonnées dans des systèmes de coordonnées distinct n'a aucun sens physique, ne peut pas correspondre à un concept pertinent. (Shakespeare et Cervantès sont décédés le même jour, le 23 avril 1616, à dix jours d'intervalle...)

[invite4a87a96d]

Ce n'est pas tout à fait ça, mais ça y ressemble.

Dans un premier temps, oubliez l'accélération.

Ensuite, il faut distinguer âge (= position dans le temps) est vieillissement (= vitesse).

La distance entre les deux jumeaux va jouer sur l'âge mais pas le vieillissement : si vous imaginez des voyageurs dans un train à une vitesse relativiste, tous les passagers vieillissent de la même façon mais ils ont tous un âge différent, les plus jeunes étant à l'avant. Lorsqu'une minute passe pour vous, tous les passagers vieillissent mettons de 30 secondes et restent donc avec leurs différence d'âge.

Maintenant si vous imaginez sauter dans le train en marche (à vos risques et périls): tous les passagers prendront l'âge du passager au niveau duquel vous avez sauté.

Alors de ce point de vue (vous avez en quelque sorte accéléré), les passagers vont changer d'âge (vieillir ou rajeunir) de façon d'autant plus importante qu'ils sont éloignés.

c'est ce que je disait..

Ce qui me gênait, c'est que les gens pouvait voyager 100 seconde à la même vitesse, choisir un repère arbitraitrement, ralentir (uniquement selon ce nouveau répère) pour l'atteindre, et avoir des ages différents (dt* 100)...
ou alors voyager 1000 000 000 seconde, choisir le même repére, ralentir (exactement de la même façon que précédemment) et se retrouver à avoir des ages beaucoup plus différent (dt * 1000 000 000).
Le même "ralentissement" pouvait donc avoir pour conséquences des différences d'age complétement différente.. (c'est qu'on imagine si on suppose "simplement" que le ralentissement "crée" la différence d'age et le conditionne).
Donc là, avec cette idée selon laquelle la distance parcouru compte aussi pendant le ralentissement (ce qui est cohérent avec la rotation des lignes de simultanéité : le ralentissement fait changer l'age, et comme les lignes "tournent" on voit que le changement dépend aussi de la distance) , on s'y retrouve..

[invite4a87a96d]

Sinon, ça n'a aucun rapport mais je pense aussi qu'il faudrait créer des genres de "F.A.Q" thématiques sur ce genre de question, plus précis que des dossiers : quand on essaye de comprendre on se dit "ça je comprend, oui mais ça je comprend pas si et si et si.. "

[invite289c27d7]

Au mieux, vous êtes en train d'assimiler E et F parce que l'un a la même coordonnée temporelle dans le système R que l'autre dans le système R'.

C’est époustouflant que vous puissiez écrire ça !

C’est à se demander si vous lisez ce que j’écris. Mon message #31 illustré d’un schéma dans lequel je définis précisément les événements E et F est là pour expliquer que justement il s’agit de deux événements différents.

Comment pouvez-vous écrire que je les assimile d’une quelconque façon !

Shakespeare et Cervantès sont décédés le même jour, le 23 avril 1616, à dix jours d'intervalle...)

Vous allez mieux comprendre avec Baez. Je reprends son schéma de la section « Too Many Analyses: a Meta Objection »



Tiré de : http://math.ucr.edu/home/baez/physic...twin_vase.html

Mes ajouts sont en rouge pour faire le lien avec ce que je dis jusqu’à présent, notamment les événements E et F que ni Baez ni moi n’assimilons en aucune façon.

J’ai bien compris que Baez considère que la seule explication est la représentation du diagramme « nu », qu’il suffit de dire que la ligne droite n’est pas le chemin le plus court entre deux événements, que les axes de simultanéité sont un choix comme un autre de décoration du diagramme.

Moi, je trouve que ça explique bien : le jumeau terrestre vieillit de plusieurs années durant le demi-tour du jumeau voyageur.