Transformée de Fourier discrète et coefficients

[Lonk]

Bonsoir à tous

Je planche actuellement sur un projet de Modulation, et je suis confronté à un petit problème ...
On doit, en s'aidant de Matlab, trouver un signal réel périodique qui donnerait une TFD ayant tous ses coefficients égaux à 1. On nous donne une fréquence d'échantillonage de 8kHz ainsi qu'un nombre de 4 échantillons.

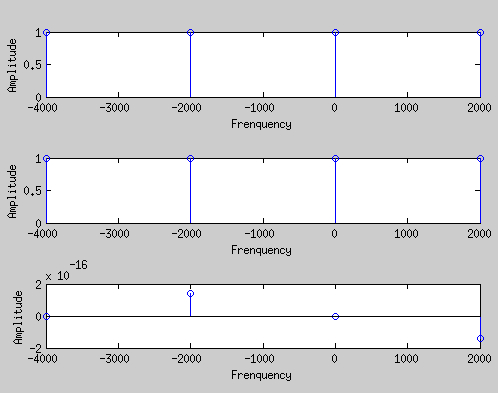
Du coup, il faut que la partie réelle (et donc le spectre) ait une valeur de 1, pour les 4 fréquences associées à mes échantillons.

J'ai trouvé que le résultat était possible si l'un des échantillons était égal à 1 tandis que les autres valent 0. ([1 0 0 0], etc ...)

C'est ici que se pose mon soucis: comment trouver un signal périodique qui, une fois échantillonné à 8kHz, donne ces 4 valeurs ? J'arrive très facilement à avoir [1 0 -1 0] avec , mais du coup, il me reste ce 1 en trop ...

J'attache en pièce jointe le sujet, si quelqu'un veut avoir tous les éléments en main. Il s'agit de la question 2 de l'exercice 1 (en anglais, désolé :3), ainsi que mon début de rapport pour vous donner mes résultats de la question 1.

Si quelqu'un a une idée

Merci beaucoup et bonne soirée,
Lonk
-----

[phuphus]

Bonsoir,

J'ai trouvé que le résultat était possible si l'un des échantillons était égal à 1 tandis que les autres valent 0. ([1 0 0 0], etc ...)

Ce serait bien que tu nous dise comment tu as trouvé cela, que nous puissions juger si tu es sur la bonne voie ou pas.

Indice : quelles sont les 4 fréquences représentées dans ton spectre ?

P.S. : pièces jointes pas encore validées, j'attendrai qu'elles le soient pour répondre plus complètement

[Lonk]

Bonsoir
Pour la première question, c'est pas glorieux: j'ai trouvé un document sur le net à propos de la DFT qui montrait ce résultat, du coup je me suis dit que j'allais me baser dessus. Et en fait, je ne sais pas du tout si c'est une bonne piste (c'est pour ça que j'ai préféré poster dans la partie physique que sur la partie mathématiques, afin d'être sûr que je ne cherche pas dans la mauvaise direction).

Les 4 fréquences sont 0, 2000, 4000 et 6000 Hz, avec un axe de symétrie à 4000 Hz si la condition de Nyquist-Shannon est respectée.

Je vais creuser du côté de "comment aboutir à [1 0 0 0]", même si je pense que ça a un lien avec la formule mathématique de la DFT (fin non, ça a forcément un lien) ou avec celle de calcul des Coefficients de Fourier.

Merci

[phuphus]

Bonsoir,

le coup du [1 0 0 0] est une bonne piste, mais là j'ai l'impression que tu réfléchis en temporel pour retrouver ce résultat, alors qu'il faudrait plutôt réfléchir en fréquentiel. Pour avoir un spectr de [1 1 1 1], quelles doivent être les amplitudes des 4 fréquences présentes dans le spectre ? Comment cela se traduit-il en temporel sachant ce que représentent ces coefficients ?

Une fois les réponses à ces question trouvées, on en viendra à l'autre interprétation du [1 0 0 0]. Sais-tu ce qu'est un bruit blanc ?

Par contre, au niveau de l'amplitude, tu dois avoir un problème de normalisation. Tu utilises la fonction Matlab "fft" ?

[A voir en vidéo sur Futura]

[Lonk]

Bonsoir

Si je ne me trompe pas, elles doivent être de 1 (partie réelle égale à 1 pour chaque échantillon, et la partie imaginaire égale à 0) ? (si ça c'est bon, déjà, ça me rassurera pas mal sur mes capacités de recherche sur google)
Pour la signification en temporel, si ce n'est que ça a un lien avec le nombre d'échantillons, je ne sais pas. On nous a un peu lâché dans la nature avec ce projet, et j'avoue avoir un peu de mal :')

Je connaissais le bruit blanc, mais pas ses propriétés ... Qui ont l'air de ressembler à ce que je cherche.

J'utilise effectivement la fonction fft de Matlab.

J'ai hebergé les deux fichiers ici si besoin est : http://klik.siteboz.fr/mc/

Merci

[b@z66]

Deux indices: un signal périodique possède des fréquences qui sont toutes multiples d'une fréquence de fondamentale qui correspond à la fréquence du signal, ta DCT a déjà ses coefficients qui correspondent à des fréquences multiples de l'écart qui les sépare.

Autre indication: la deuxième partie de ton exercice ne doit rien à voir avec sa première partie puisque dans la première partie on a une "8-DCT" et dans la deuxième une "4-DCT".

PS: la fonction fft de matlab n'était pas normalisée dans mon souvenir. Il faut sans doute rajouter cette normalisation à la main.

[Lonk]

Bonsoir,

Effectivement, la réponse me pendait sous le nez ... Merci beaucoup pour le premier indice

Je trouve donc :
x = cos(2*pi*2000*t) + cos(2*pi*4000*t)+ cos(2*pi*6000*t) + cos(2*pi*8000*t);

Là, j'ai tous les coefficients égaux à 4, comme vu précédemment. Du coup, il me suffit de mettre un facteur 1/4:
x = (1/4)*(cos(2*pi*4000*t) + cos(2*pi*6000*t)+ cos(2*pi*2000*t) + cos(2*pi*8000*t));

Et là, tout baigne

Merci beaucoup pour votre aide à tous les deux !

Lucas

[Lonk]

Et je me permet de reposter pour apporter quelques corrections aux futures personnes qui passeraient après moi :P

J'ai finalement utilisé fftshift, et changé mon échelle de fréquences, pour centrer le spectre en 0. Du coup, j'ai utilisé les fréquences 0 (et cos(0) = 1 donc ... x)) qui donne une amplitude de 4, 2000 qui donne une amplitude de 2 (car le nombre d'échantillons est divisé entre lui et son image), un deuxième signal fréquencé à 2000Hz pour compenser ce qui est dit précédemment, et un signal à 4000Hz

Le résultat est celui-là:


Un dernier merci à vous deux, et sûrement à la prochaine vu l'ampleur de la tâche qui m'attend pour la suite de ce rapport

[b@z66]

Bonsoir,

Effectivement, la réponse me pendait sous le nez ... Merci beaucoup pour le premier indice

Je trouve donc :
x = cos(2*pi*2000*t) + cos(2*pi*4000*t)+ cos(2*pi*6000*t) + cos(2*pi*8000*t);

Là, j'ai tous les coefficients égaux à 4, comme vu précédemment. Du coup, il me suffit de mettre un facteur 1/4:
x = (1/4)*(cos(2*pi*4000*t) + cos(2*pi*6000*t)+ cos(2*pi*2000*t) + cos(2*pi*8000*t));

Et là, tout baigne

Merci beaucoup pour votre aide à tous les deux !

Lucas

Il me semble que la normalisation n'était à faire que dans le sens signal temporel vers fft et non l'inverse. Tu devrais à mon avis pouvoir utiliser les coefficients tel quel pour la reconstruction temporelle du signal(encore qu'il y ait la possibilité de la présence d'un coefficient 1/2 qui prennent en compte les fréquences négatives). Sinon, encore une remarque,

x = 1+ cos(2*pi*2000*t) + cos(2*pi*4000*t)+ cos(2*pi*6000*t) est aussi une possibilité de signal temporel et périodique donnant le même résultat(du au recouvrement de spectre): le fait d’échantillonner 1 ou cos(2*pi*8000*t) à 8KHz revient au même.

[b@z66]

Pour tout dire, tu dois reprendre tous les graphiques de ta première question en introduisant la normalisation dans la FFT(par exemple dans le petit a où tu as trouvé une composante continue égale à 8 alors que tu as échantillonné un signal égal à 1...). Tu as d'ailleurs un exemple ici. Enfin, le coefficient 1/2 doit bien être présent à mon avis de part la considération des fréquences négatives. Je te suggérerais plutôt donc, pour ta deuxième question, le résultat suivant qui ne prend en compte que la moitié des coefficients de part les symétries dans le spectre du signal échantillonné.

x = 1+ 2.cos(2*pi*2000*t) + cos(2*pi*4000*t)

Tu remarqueras que ce signal respecte la condition de Nyquist-Shannon pour se caractériser(en réalité, on doit pouvoir sinon construire une infinité de signaux continus qui respectent le résulatat de la 4-DCT). Pour te faire à l'idée, tu peux simplement t'imaginer le résultat de l’échantillonnage de cette fonction(périodisation du spectre) pour comprendre comment on retrouve les 4 coefficients égaux à 1. Personnellement, je ne suis pas arrivé à retrouver ce résultat par le calcul mais la démarche graphique est pour le coup beaucoup plus explicite.

PS: DCT est normalement le symbole de Discrete Cosinus Transform qui n'est pas LA transformée de Fourier discrète à proprement parler.

[b@z66]

PS: DCT est normalement le symbole de Discrete Cosinus Transform qui n'est pas LA transformée de Fourier discrète à proprement parler.

Excuse de ma part, c'est moi qui ait confondu DFT dans tes questions avec DCT.

[phuphus]

Bonjour,

le fonction "fft" dans Matlab n'est en effet pas normalisée. Le tout est de savoir ce que l'on veut obtenir : la fft n'est qu'un outil de base dont les interprétations diffèrent en fonction du contexte. ici, il est pour moi implicite que l'on cherche un spectre d'amplitudes, donc que chaque coef reflète l'amplitude de la composante cosinusoïdale réelle du signal. Il faut donc de base diviser par le nombre de points de la fft pour trouver les bons coefficients, c'est à dire ceux qui correspondent à chaque composante cos dans Matlab (et éventuellement ajouter un facteur 1/2 supplémentaire dans le cas d'un signal réel dont on voudrait tracer le spectre en respectant la condition de Shannon...).

Dans ce cadre, on associe donc directement l'amplitude du point considéré dans le spectre à l'amplitude du cos temporel. Mais ce n'est qu'un cas particulier, il y en a d'autres (spectre de puissance, d'énergie, etc.).

Les 4 fréquences sont 0, 2000, 4000 et 6000 Hz

OK, donc pourquoi fais-tu cela :

x = cos(2*pi*2000*t) + cos(2*pi*4000*t)+ cos(2*pi*6000*t) + cos(2*pi*8000*t)

Bien entendu, on retombe sur le résultat puisque le spectre d'un signal discret est périodique (donc 0 Hz et 8 000 Hz, c'est pareil dans ce cas), mais j'ai l'impression que là tu as surtout cherché à retrouver de manière empirique le signal temporel [4 0 0 0] plutôt que réellement comprendre ce que tu fais.

x = 1+ 2.cos(2*pi*2000*t) + cos(2*pi*4000*t)

Lonk, as-tu compris ce résultat ? Tu peux l'approcher de deux manières différentes :
1 - Tracer sur des graphes distincts chaque composante cos du signal, et comparer les allures de cos(2*pi*2000*t) et cos(2*pi*6000*t). Conclure.
2 - Comme le suggère b@zz66, utiliser les propriétés de la DFT : le spectre d'un signal réel est symétrique conjugué (et comme ici les coefs sont réels...), et / ou le spectre d'un signal discret est périodique

Tu remarqueras que ce signal respecte la condition de Nyquist-Shannon pour se caractériser(en réalité, on doit pouvoir sinon construire une infinité de signaux continus qui respectent le résulatat de la 4-DCT)

Il y a une infinité d'équations permettant d'obtenir le signal temporel donnant le spectre réel [1 1 1 1], mais il y a un seul et unique signal temporel associé à cette DFT.

Au niveau interprétation, le signal temporel en question est l'équivalent numérique d'un delta de Dirac, qui par définition possède un spectre constant. On voit bien ici qu'un Dirac est un bruit blanc "phasé" : toutes les composantes fréquentielles ont une phase à l'origine nulle.

[Lonk]

Bonsoir à tous les deux.
Tout d'abord merci pour vos réponses

Concernant vos réactions sur mon deuxième exercice, j'avais effectivement compris le résultat "x = 1+ 2.cos(2*pi*2000*t) + cos(2*pi*4000*t)" puisque c'est celui que j'ai utilisé dans mon deuxième post (mon correctif, après avoir centré ma DFT). Et j'avais aussi rédigé toute l'explication qui colle à ta deuxième manière d'aborder le sujet (celle de b@zz66)
Pour la normalisation, je vais l'appliquer sur mes exos, merci pour le lien mathworks

Pour répondre à ta première question, j'avais utilisé 8000 car le signal étant périodique, et 8000 ma fréquence d'échantillonage, je revenais au même. Je n'avais pas testé avec 0, et avait répondu vite, n'ayant pas énormément de temps au moment où je l'ai fait

Je posterais dans la soirée ce que j'ai re-rédige grace à votre aide, pour voir si j'ai bien compris

Bonne soirée

[Lonk]

Bonsoir
Voilà ce que donnent mes deux premières questions après un remaniement en profondeur suite à vos remarques
J'ai globalement compris ce qu'est le spectre d'amplitude (en gros, on donne l'amplitude d'un signal qui a une certaine fréquence ? Un sinus/un cosinus ayant une amplitude de 2, je me suis servi du a de ma question 1 pour normer ma DFT).

Pardonnez ma façon d'écrire en anglais maladroite, j'étais très fatigué aujourd'hui, et je compte relire pour rendre ça un peu plus fluide

Bonne soirée !
Lucas

[b@z66]

Bonsoir
Voilà ce que donnent mes deux premières questions après un remaniement en profondeur suite à vos remarques
J'ai globalement compris ce qu'est le spectre d'amplitude (en gros, on donne l'amplitude d'un signal qui a une certaine fréquence ?

Pas tout à fait, avec cette DFT, les harmoniques de ton signal se retrouve chacune décomposées suivant deux exponentielles complexes, une de fréquence négative et l'autre de fréquence positive. L'amplitude d'un harmonique "réel"(cosinus) se retrouve donc réparti sur ces deux fréquences(formule de Euler), c'est la raison pour laquelle les coefficients qui apparaissent dans ta DFT sont moitié moindre que l'amplitude de tes signaux réels de départ.

Un sinus/un cosinus ayant une amplitude de 2, je me suis servi du a de ma question 1 pour normer ma DFT).

Tu as bien fait puisque c'est l'exception à ma remarque précédente: l'amplitude de la composante continue continue se retrouve intégralement dans le même coefficient(la fréquence négative de cette composante est confondu avec sa positive puisqu'elle est nulle!). Si la logique est respectée(ton document n'a pas encore été validé par le forum), tu as du diviser ta fft par le nombre d'échantillon présent au départ.

Pardonnez ma façon d'écrire en anglais maladroite, j'étais très fatigué aujourd'hui, et je compte relire pour rendre ça un peu plus fluide

Ne t'en fais pas, je ne saurais déjà pas en faire autant niveau vocabulaire et, bon, ça reste de l'anglais technique...

[Lonk]

Bonjour,

Merci pour ces précisions, je mettrais à jour mon rapport en en tenant compte (et notamment la formule d'Euler pour justifier la division par 2 de l'amplitude)

Je ne sais pas si je dois créer un nouveau sujet pour poser ma question suivante ou pas, un modérateur me corrigera si je me trompe mais:
Il n'y aurait-il pas un soucis dans l'énoncé de mon exercice 2 ? En effet, quand je regarde sur les différentes sources que je trouve à propos du sous-échantillonnage, ils prennent toujours en compte que la BP, c'est la fréquence haute moins la fréquence basse, donc dans mon cas, ça donnerait 8Hz. Mais le sujet propose 12Hz ... Est-ce que ça vous semble normal ? (en sachant que quand je fais la DFT, la distance entre 0 et l'harmonique liée à 128Hz est de 12Hz ... Mais que pour un échantillonnage à 29Hz - et pas à 25Hz-, j'ai bien une distance de 8Hz entre l'harmonique du signal à 120Hz et celui à 128Hz)

Re-merci d'avance

Lucas