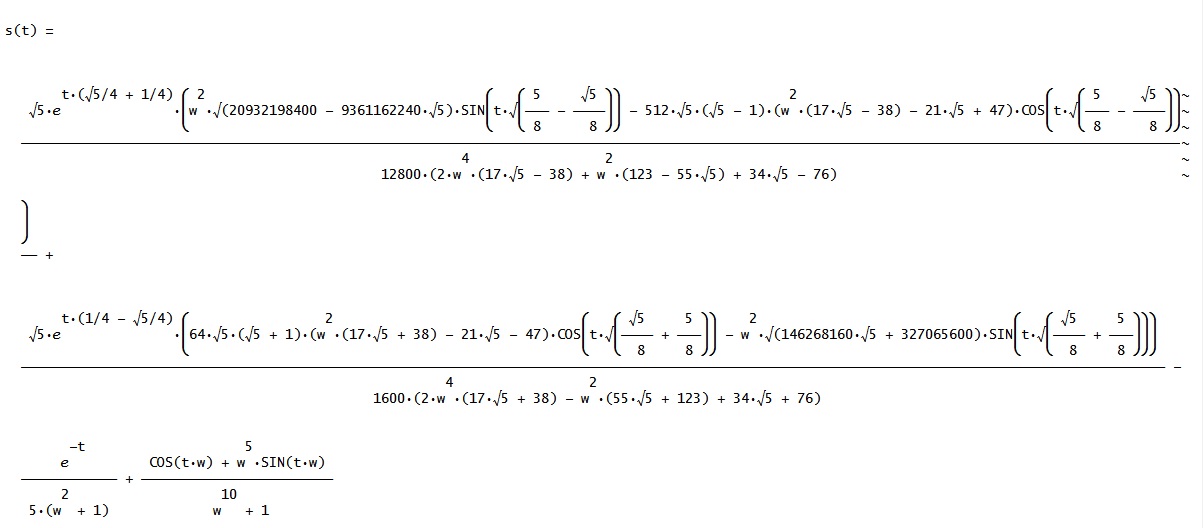Causalité / instabilité du système défini par H(ω)=1/(1+(jω)^5)

[phuphus]

Bonsoir,

@ phuphus :
Comme tu dis, la question n'est pas triviale, et on dirait même que tout n'est pas parfaitement clair pour les personnes qui publient les critères de stabilité. Je veux dire que tout n'est pas forcément expliqué avec une grande rigueur.

Oui, j'ai consulté pas mal de sources différentes avant d'avoir une synthèse cohérente. Personne ne présente une vue d'ensemble claire, et certains font de gros raccourcis.

Ici, c'est A(w) qui vaut 1 et B(w) qui vaut j.w^5. Mais ça n'est pas lié à Nyquist, mais au gain en boucle ouverte T(w)=A(w).B(w).

Il me semble que dans la notation que tu utilises avec A(ω) et B(ω), le gain de contre-réaction est B(ω). Nyquist est valable pour une gain de contre-réaction unitaire.
http://www.upsti.fr/scenari/module_f...Contenu93.html

La TLI, est la transformée de Laplace inverse.

Merci !

Je te cite :"Oui, un pôle complexe est bien un pôle, et c'est bien la partie réelle qui est importante pour la stabilité." Tu piques ma curiosité là dessus, car c'est le nerf de la guerre. La partie imaginaire doit elle être nulle ou pas ? J'en ai conclu à mon dernier post que oui. Mais si tu peux apporter des éléments, c'est avec plaisir.

Je suis sur le critère de stabilité "classique" : pour avoir une stabilité EBSB (Entrée Bornée Sortie Bornée), la zone de convergence de la transformée de Laplace doit être située dans le demi-plan complexe positif. S'il existe donc un seule pôle à partie réelle positive, cela veut dire qu'il y a dans le demi-plan positif au moins un point pour lequel l'intégrale définissant la transformée de Laplace n'est pas définie : la zone de convergence ne couvre donc pas tout le demi-plan. D'où le critère classique des pôles à partie réelle négative.

Quand tu regardes l'intégrale complète, et que tu remplaces la variable "p" par a+ib, tu remarques qu'une TL est une TF pour laquelle on rajoute un terme soit "d'amplification" (a < 0), soit "d'amortissement" (a > 0). Si on a besoin "d'amplifier" avec une exponentielle positive la réponse impulsionnelle pour ne pas faire converger sa TL (en d'autres termes si l'on a que des pôles à partie réelle négative, puisque l'on a "-p" dans l'intégrale), c'est que le système est stable de base.

Enfin, si H était instable, j'aimerais au moins que l'on puisse mettre un contre exemple en évidence.

C'est à dire trouver une entrée pour laquelle l'intégrale converge ?
-----

[phuphus]

Bonsoir,

Tout simplement parce que, comme indiqué précédemment, en faisant une TF inverse ou une TL inverse, on fait des hypothèses implicites(l'original d'une TF tend vers 0 pour pour t allant vers + ou - l'infini tandis que l'original d'une TL est nulle pour t négatif). Les deux hypothèses pouvant se contredire, comme deux conditions initiales contradictoires, les résultats de transformée inverse à partir d'une TL et d'une TF d'une même fonction de transfert peut donner des résultats différents en tant que réponse impulsionnelle.
[...]
Comme dit plus haut, les TL et TF font des hypothèses implicites différentes sur les signaux de départ, le résultat de leur transformée inverse d'une même fonction de transfert peut donc être différent.

Le problème est que tu fais les TL et TF inverses de deux fonctions de transfert qui ne sont pas les mêmes.
Les fonctions H1 et G1 que j'ai écrites en #7 ne sont pas des fonctions de transfert du même système. Il ne faut pas se laisser abuser par le formalisme. En fait, nous sommes d'accord sur "en faisant une TF inverse ou une TL inverse, on fait des hypothèses implicites", nous ne sommes juste pas d'accord sur l'interprétation que l'on doit en faire ; quoique :

une propriété intrinsèque d'un système physique ne doit pas dépendre du fait que l'on utilise tel ou tel outil mathématique abstrait(TL ou TF)

Entièrement d'accord !

Et de ce point de vue, ce qui caractérise totalement un système LTI est sa RI. Si H1 et G1 ne donnent pas les mêmes RI, c'est qu'elles ne représentent pas le même système.

Faux, je te le prouve en deux coups de cuillère à pot. La fonction de transfert d'un circuit RC du 1er ordre (à résistance positive) peut s'écrire FTstable(w)=1/(1+tau.jw), sa réponse impulsionnelle vaut 0 pour t négatif et (1/tau)e(-t/tau) pour t positif. Dans le cas d'un circuit RC à résistance négative, on considère donc que R change de signe et donc que la constante de temps tau change aussi de facto de signe. On peut résumer ça par la fonction de transfert de ce circuit RC à résistance négative qui s'écrit donc FTinstable(w)=1/(1-tau.jw) en tentant de garder la même valeur algébrique pour tau que dans l'expression de la première fonction de transfert citée. Tu devrais remarquer tout de suite que FTstable(f)=FTinstable(-f) or tu as, dans les tables de propriétés de la TF, une propriété qui dit que la transformée inverse de fourier de H(-f) est h(-t)(en considérant que H(f) est la transformée de Fourier de h(t)). J'ai fait le gros du raisonnement, je te laisse le conclure.

C'est bien ce que j'avais compris ici, et je ne sais pas si ma manière de conclure va te plaire

Tu viens de "montrer" que (je pose tau=1 pour plus de simplicité) :



Sachant que la TF est bijective, c'est gênant.

Peux-tu aussi me confirmer que pour toi, la TF de exp(t).H(t) existe ?

Pour en revenir à quelque chose d'intéressant que tu as mentionné, le ROC(le domaine de convergence, j'imagine) d'une fonction de transfert d'un système n'a pas en soi à être limité d'une façon ou d'une autre du fait que l'on utilise soit Fourier, soit Laplace. La fonction de transfert caractérise fondamentalement une propriété intrinsèque à la dynamique d'un système or une propriété intrinsèque d'un système physique ne doit pas dépendre du fait que l'on utilise tel ou tel outil mathématique abstrait(TL ou TF).

Ce n'est en effet pas l'utilisation de Laplace ou de Fourier qui donne la zone de convergence de l'intégrale, mais bien la RI du système + le calcul mathématique. Tu ne peux pas poser p = jω alors que pour Re(p)=0 l'intégrale définissant la TL ne converge pas : si l'axe de imaginaires purs n'est pas dans la ROC de la TL, la RI du système n'admet pas de TF. C'est une autre formulation de ce que tu as déjà écrit par ailleurs (tu avais écrit "la RI doit s'atténuer en +/-inf", il me semble).

[b@z66]

Et de ce point de vue, ce qui caractérise totalement un système LTI est sa RI. Si H1 et G1 ne donnent pas les mêmes RI, c'est qu'elles ne représentent pas le même système.

C'est bien ce que j'avais compris ici, et je ne sais pas si ma manière de conclure va te plaire

Tu viens de "montrer" que (je pose tau=1 pour plus de simplicité) :



Sachant que la TF est bijective, c'est gênant.
Peux-tu aussi me confirmer que pour toi, la TF de exp(t).H(t) existe ?

Pas du tout, tu n'as pas du tout bien lire mon dernier commentaire, cela n'a rien a voir avec une bijectivité. Je te démontrais que la transformée de fourier inverse de la fonction de transfert d'un circuit RC instable existe contrairement à ce que tu affirmes dans un de tes précédents post Pour preuve, je te donne le résultat final(en posant tau=1 pour faire simple) vu que tu n'as pas fait le raisonnement jusqu'au bout. On reconnaît d'ailleurs bien le comportement instable avec cette divergence en sortie avant que l'on applique l'impulsion en entrée.
Je te confirme donc que la TF inverse de la fonction de transfert est bien exp(t).H(-t).
De même, Je te confirme que la TL inverse de cette même fonction de transfert est exp(t).H(t).

Ce n'est en effet pas l'utilisation de Laplace ou de Fourier qui donne la zone de convergence de l'intégrale, mais bien la RI du système + le calcul mathématique. Tu ne peux pas poser p = jω alors que pour Re(p)=0 l'intégrale définissant la TL ne converge pas : si l'axe de imaginaires purs n'est pas dans la ROC de la TL, la RI du système n'admet pas de TF. C'est une autre formulation de ce que tu as déjà écrit par ailleurs (tu avais écrit "la RI doit s'atténuer en +/-inf", il me semble).

Non, ce n'est pas la réponse impulsionnelle qui caractérise la dynamique du système puisque je viens de te démontrer qu'elle n'est pas unique suivant les outils mathématiques utilisés mais bien la fonction de transfert.

[b@z66]

Non, ce n'est pas la réponse impulsionnelle qui caractérise la dynamique du système puisque je viens de te démontrer qu'elle n'est pas unique suivant les outils mathématiques utilisés mais bien la fonction de transfert.

Ou plutôt, si. La réponse impulsionnelle caractérise aussi bien le système mais en gardant bien à l'esprit qu'elle n'est pas unique et que l'exemplaire particulier qu'on utilise dépend avant tout de la transformée utilisée. Le fait que la fonction de transfert, elle, soit vraiment unique est quelque chose qui me fait dire qu'elle est beaucoup plus représentative puisque indépendante des outils mathématiques utilisés.

[stefjm]

Ou plutôt, si. La réponse impulsionnelle caractérise aussi bien le système mais en gardant bien à l'esprit qu'elle n'est pas unique et que l'exemplaire particulier qu'on utilise dépend avant tout de la transformée utilisée.

Je ne comprends rien à ce que tu dis là...
La réponse impulsionnelle d'un système n'est plus unique? J'en apprend un peu chaque jour.
delta(t) en entrée donne ri(t) en sortie.
Je ne vois pas pourquoi la ri(t) devrait dépendre des TF ou TL utilisée parce que les projections fréquentielles des signaux sont plus facile à manipuler que les projections temporelles.

Le fait que la fonction de transfert, elle, soit vraiment unique est quelque chose qui me fait dire qu'elle est beaucoup plus représentative puisque indépendante des outils mathématiques utilisés.

Cette inversion me parait curieuse.
Je vais tout relire pour essayer de comprendre le point de vu.
Cordialement.

[b@z66]

Je ne comprends rien à ce que tu dis là...
La réponse impulsionnelle d'un système n'est plus unique? J'en apprend un peu chaque jour.
delta(t) en entrée donne ri(t) en sortie.
Je ne vois pas pourquoi la ri(t) devrait dépendre des TF ou TL utilisée parce que les projections fréquentielles des signaux sont plus facile à manipuler que les projections temporelles.

L'expression de la TL et la TF sont des cas particuliers de transformée bilatérale de Laplace dont l'expression ne définit pas de manière univoque par son expression une réponse impulsionnelle donnée

Cette inversion me parait curieuse.
Je vais tout relire pour essayer de comprendre le point de vu.
Cordialement.

La TF et la TL imposent implicitement des conditions différentes sur les réponses impulsionnelles. C'est comme lorsque l'on impose des conditions initiales différentes dans une équation différentielle, la solution de l'équation ne reste pas nécessairement la même et ce même si la dynamique du système reste la même.

[phuphus]

Bonjour,

Pas du tout, tu n'as pas du tout bien lire mon dernier commentaire, cela n'a rien a voir avec une bijectivité.

C'est bien cela qui me dérange : tu ne vois pas le problème de ton raisonnement avec la bijectivité de la TF.

Je te démontrais que la transformée de fourier inverse de la fonction de transfert d'un circuit RC instable existe contrairement à ce que tu affirmes dans un de tes précédents post

Je n'ai jamais affirmé cela : merci de me citer pour prouver tes dires.
J'affirme que la TF directe de la RI d'un circuit RC instable n'est pas définie.

Pour preuve, je te donne le résultat final(en posant tau=1 pour faire simple) vu que tu n'as pas fait le raisonnement jusqu'au bout.

Là, c'est insultant. Je te mets noir sur blanc le résultat du raisonnement en question (membre de droite de l'équation que je donne en #32), et non seulement tu passes à côté mais en plus tu affirmes que je n'ai pas su mener le raisonnement à terme.

On reconnaît d'ailleurs bien le comportement instable avec cette divergence en sortie avant que l'on applique l'impulsion en entrée.
Je te confirme donc que la TF inverse de la fonction de transfert est bien exp(t).H(-t).
De même, Je te confirme que la TL inverse de cette même fonction de transfert est exp(t).H(t).

Diantre ! Les membres respectivement de droite et de gauche de mon équation en #32. Sauf que la manière dont j'ai écrit l'équation sous-entend que je prends directement la réponse temporelle du circuit RC instable, sans passer par la TL inverse (mais c'est pareil : le système est causal, on a le droit d'utiliser la TL monolatérale). Vois-tu donc ainsi que j'ai parfaitement compris ton raisonnement ?

A toi maintenant de comprendre le mien.

Non, ce n'est pas la réponse impulsionnelle qui caractérise la dynamique du système puisque je viens de te démontrer qu'elle n'est pas unique suivant les outils mathématiques utilisés mais bien la fonction de transfert.

Je comprends bien que tu considères que 1/(1-jw) et 1/(1-p) sont les mêmes fonctions de transfert, et que pour toi pouvoir interchanger sans aucune condition "p" et "jw" est un principe. Si tu restes sur ce principe, la discussion tournera en boucle : pas la peine de l'alimenter plus.

[stefjm]

Je comprends bien que tu considères que 1/(1-jw) et 1/(1-p) sont les mêmes fonctions de transfert, et que pour toi pouvoir interchanger sans aucune condition "p" et "jw" est un principe. Si tu restes sur ce principe, la discussion tournera en boucle : pas la peine de l'alimenter plus.

Quelle sont les EDO de ces deux systèmes? (celle en p, je sais faire, celle en jw, je ne sais plus trop...)

[polf]

J'ai essayé une résolution temporelle un peu différente de celle que j'avais faite.

Comme H peut s'écrire H=1/((p-p0).(p-p1).(p-p2).(p-p3).(p-p4))
pi pôles pouvant être comlexes

et que : e^(a.t) C 1/(p-a) C est la TL

Alors, en prenant soin de bien déterminer les bornes, on a :

s(t) = e^(p0.t) * e^(p1.t) * e^(p2.t) * e^(p3.t) * e^(p4.t) * e(t) où * est le produit de convolution

Je choisis e(t) = cos(w.t+phi)

Mais les calculs deviennent vite énormes....

[polf]

Toujours en restant sur l'idée du produit de convolution, mais en associant les pôles imaginaires 2 à 2, j'ai pu intégrer le bouzin.
Les calculs étant vraiment ENORMES, et je les ai fait avec un logiciel de calcul analytique qui lui-même n'en pouvait plus, et en espérant qu'aucune erreur ne se soit glissée :
Il me reste 3 termes : 1 terme stable en 1/(1+w^10) , 1 terme en exponentielle négative et un terme en exponentielle positive. Ce dernier fait diverger s(t) quelle que soit la pulsation w.
Le terme en exponentielle positive est directement lié aux pôles de partie réelle positive - quand bien même ceux ci ne sont pas réels purs.

Pour le plaisir (je vous assure, si, si, que le résultat final s'est grandement simplifié par rapport aux calculs intermédiaires pour aboutir à ceci :


On retrouve le terme que j'avais obtenu par résolution de l'équa diff du système issue de Laplace : s'''''+s=e. C'est le dernier terme. Mais d'autres termes se rajoutent ici.

Evidemment, ceci est instable !

Pour moi, le résultat est enfin clair, et .... incontestable (??) !

[stefjm]

J'ai essayé une résolution temporelle un peu différente de celle que j'avais faite.
Comme H peut s'écrire H=1/((p-p0).(p-p1).(p-p2).(p-p3).(p-p4))
pi pôles pouvant être comlexes
et que : e^(a.t) C 1/(p-a) C est la TL
Alors, en prenant soin de bien déterminer les bornes, on a :
s(t) = e^(p0.t) * e^(p1.t) * e^(p2.t) * e^(p3.t) * e^(p4.t) * e(t) où * est le produit de convolution
Je choisis e(t) = cos(w.t+phi)

En version TL, cela donne
cos t devient p/(1+p^2)
qu'on multiplie par 1/(1+p^5) pour obtenir la réponse au cosinus
Il suffit de prendre TL-1 pour retrouver la réponse temporelle.
Voir ici le calcul.
Réponse évidement divergente donc 1/(1+p^5) instable, correspondant sans doute à ce qu'a trouvé polf.
http://forums.futura-sciences.com/ph...ml#post5099011

Mais les calculs deviennent vite énormes....

C'est bien pour cela qu'on ne les fait jamais et qu'on utilise la TL et TL-1 en automatique pour traiter du système
(Les convolutions temporelles deviennent des produits fréquentiels.)

1/(1+p^5) correspond à l'équation différentielle


@ phuphus
Pour toi, quelle est l'équation différentielle correspondante à H1?


Puisque tu dis que H1 et G1 sont deux systèmes différents, il me semble qu'il est primordial de répondre à cette question.

Je vais relire tout le fil et répondre aux points qui me paraisse curieux.

Je peux déjà dire que la différence entre p et jw se trouve dans les concepts de phases déroulées (pour p) et de phase périodique (pour jw)
On perd de l'information quand on écrit (jw)^4=w alors qu'on n'en perd pas avec p^4.
Edit : http://forums.futura-sciences.com/ma...rap-phase.html

L'avis de MiPaMa serait précieux.
Je vais faire un cross postage sur math pour signaler ce fil.

Cordialement.

[phuphus]

Bonjour,

Je comprends bien que tu considères que 1/(1-jw) et 1/(1-p) sont les mêmes fonctions de transfert, et que pour toi pouvoir interchanger sans aucune condition "p" et "jw" est un principe. Si tu restes sur ce principe, la discussion tournera en boucle : pas la peine de l'alimenter plus.

A la relecture, ma dernière phrase n'est pas claire ; b@z66, je ne veux surtout pas dire par là que ce n'est plus la peine que tu interviennes sur ce fil, bien au contraire. Je signifie juste que toi comme moi n'avons pas intérêt à "alimenter la boucle".

Surtout que vues les dernières interventions de stefjm, je sens que ceci va bientôt être utile :

En effet, on peut très bien interpréter cette réponse anti-causale comme le résultat d'une perturbation infinitésimale dont l'origine est repoussée en t=-infini et l'impulsion en t=0 n'aurait pour effet que de remettre dans un équilibre idéal la sortie qui système qui reste ensuite à partir de t=0 à une valeur parfaitement nulle.

[phuphus]

Bonjour,

Quelle sont les EDO de ces deux systèmes? (celle en p, je sais faire, celle en jw, je ne sais plus trop...)

A vue de pif : les mêmes.

Où l'on sait déjà sur quoi va porter la suite de la discussion... (faire des maths ou faire de la physique, that is the question)

[stefjm]

Surtout que vues les dernières interventions de stefjm, je sens que ceci va bientôt être utile :

Envoyé par b@z66
En effet, on peut très bien interpréter cette réponse anti-causale comme le résultat d'une perturbation infinitésimale dont l'origine est repoussée en t=-infini et l'impulsion en t=0 n'aurait pour effet que de remettre dans un équilibre idéal la sortie qui système qui reste ensuite à partir de t=0 à une valeur parfaitement nulle.

Ce à quoi j'avais répondu ceci qui reste toujours valable aujourd'hui :

Bonjour,
J'ai trouvé ce qui me gênait dans ton document.
Pour moi, un système stable est un système dont la sortie reste bornée pour toutes entrées bornées.
Pas "il existe au moins une" mais toutes...
Je vois donc le système 1/(p-1) comme instable et causal.
Cordialement.

A vue de pif : les mêmes.

Du coup, je ne comprend plus ce que tu veux dire par :

[...]




ne sont pas issues de la même RI, donc ne représentent pas le même système.
[...]

Si c'est la même équa diff, c'est la même RI... mais pas le même système?
Cordialement.

[phuphus]

Bonjour,

J'ai essayé une résolution temporelle un peu différente de celle que j'avais faite.

Comme H peut s'écrire H=1/((p-p0).(p-p1).(p-p2).(p-p3).(p-p4))
pi pôles pouvant être comlexes

et que : e^(a.t) C 1/(p-a) C est la TL

Alors, en prenant soin de bien déterminer les bornes, on a :

s(t) = e^(p0.t) * e^(p1.t) * e^(p2.t) * e^(p3.t) * e^(p4.t) * e(t) où * est le produit de convolution

Je choisis e(t) = cos(w.t+phi)

Mais les calculs deviennent vite énormes....
[...]
Toujours en restant sur l'idée du produit de convolution, mais en associant les pôles imaginaires 2 à 2, j'ai pu intégrer le bouzin.
Les calculs étant vraiment ENORMES, et je les ai fait avec un logiciel de calcul analytique qui lui-même n'en pouvait plus, et en espérant qu'aucune erreur ne se soit glissée :
Il me reste 3 termes : 1 terme stable en 1/(1+w^10) , 1 terme en exponentielle négative et un terme en exponentielle positive. Ce dernier fait diverger s(t) quelle que soit la pulsation w.
Le terme en exponentielle positive est directement lié aux pôles de partie réelle positive - quand bien même ceux ci ne sont pas réels purs.

Pour le plaisir (je vous assure, si, si, que le résultat final s'est grandement simplifié par rapport aux calculs intermédiaires pour aboutir à ceci :
Sans titre.jpg

On retrouve le terme que j'avais obtenu par résolution de l'équa diff du système issue de Laplace : s'''''+s=e. C'est le dernier terme. Mais d'autres termes se rajoutent ici.

Evidemment, ceci est instable !

Pour moi, le résultat est enfin clair, et .... incontestable (??) !

J'avais aussi tenté du temporel en calcul formel la semaine dernière, mais devant l'expression imbitable obtenue (et tu obtiens de même un machin franchement indigeste) j'avais arrêté cette voie. Ici, tu pars sur du Laplace pour la résolution temporelle ; sans avoir vérifié / refait tes calculs, je trouve cela normal que tu tombes sur la version instable : c'est cohérent avec le code Matlab que j'avais mis au tout début.

Mais j'ai bien défini le système par H(ω).

Ceci dit, on peut faire dériver le sujet sur : "Instable en p = non causal en jω ?"

[polf]

Super ton site stefjm ! On retrouve bien la même expression que ce que j'avais trouvé, ce qui confirme définitivement la divergence.

le w ne passe avec p/(p^2+w^2), mais on retrouve bien la même forme.


Pour la question de causalité, elle ne s'applique qu'aux fonction e(t) et s(t), c'est un choix de l'utilisateur.

1/(1+p^5) est instable. Il existera pourtant certainement des fonctions e(t) bornées telles que s(t) soit bornée. Pas cos(wt+phi), mais une fonction qui compensera l'instabilité en permanence -> équilibre instable. Donc H instable n'empêche pas e et s non causales.

[phuphus]

Bonjour,

Ce à quoi j'avais répondu ceci qui reste toujours valable aujourd'hui :
Bonjour,
J'ai trouvé ce qui me gênait dans ton document.
Pour moi, un système stable est un système dont la sortie reste bornée pour toutes entrées bornées.
Pas "il existe au moins une" mais toutes...
Je vois donc le système 1/(p-1) comme instable et causal.
Cordialement.

Oui, tu avais répondu sur l'aspect EBSB et je suis d'accord avec cela. Mais je pense que l'on va dériver sur l'interprétation de b@z66 (car il s'agit bien d'une interprétation, donc sujette à discussion) pour d'autres raisons que le simple critère EBSB. Désolé d'être évasif, on verra quand on y sera.

Si c'est la même équa diff, c'est la même RI... mais pas le même système?
Cordialement.

Ta question en #38 portait sur le circuit RC à résistance négative, je vais continuer dessus pour la présente réponse (c'est plus simple, et l'esprit est le même).

Remarque : je reprends la notation de Wolframalpha pour l'échelon unité, c'est à dire

Equation (1), EDO :



Equation (2), pour la réponse impulsionnelle :



Les deux fonctions suivantes sont solutions de l'équation (2) :





(Du coup, y'a une erreur de signe dans les messages #32 et #33 pour les RI en Laplace...)

=> une seule EDO, au moins 2 RI, au moins 2 systèmes...

Question supplémentaire pour tout le monde : sachant que la TL (monolatérale) va de pair avec un système causal, et que la TF n'est pas convergente si la RI ne s'atténue pas en +/-inf, devinez quelle RI on va implicitement choisir en prenant soit la TF soit la TL ? A remettre en perspective avec #1 et la figure présentée.

[stefjm]

Pour la question de causalité, elle ne s'applique qu'aux fonction e(t) et s(t), c'est un choix de l'utilisateur.

C'est effectivement un choix.
La notion de causalité s'étend aux fonctions de transfert : Celle qui ont une RI causale.
http://fr.wikipedia.org/wiki/Fonctio...Causalit.C3.A9

1/(1+p^5) est instable. Il existera pourtant certainement des fonctions e(t) bornées telles que s(t) soit bornée. Pas cos(wt+phi), mais une fonction qui compensera l'instabilité en permanence -> équilibre instable. Donc H instable n'empêche pas e et s non causales.

Exhibe cette fonction et je te croirai.

Je sens que tu va chercher une solution en ajustant finement les conditions initiales.
Or pour la stabilité, ce n'est pas une solution mais toute solution. (autrement dit, CI nulle ou quelconque)

Tout ce qu'on peut faire pour stabiliser, c'est de mettre en entrée un signal RI de 1+p^5, ie delta^(5)(t)+delta(t), ce qui n'est pas terrible.
(et comme c'est en boucle ouverte, cela divergera quoi qu'il arrive un jour...)

Cordialement.

[stefjm]

Mais j'ai bien défini le système par H(ω).

Donc des éventuelles pertes de phase de 2.k.pi puisque (jw)^4=w^4.

Ceci dit, on peut faire dériver le sujet sur : "Instable en p = non causal en jω ?"

C'est toi qui voit. Cela plaira à b@z66.

En fait, je ne sais pas répondre à ton sondage car je ne vois pas trop de quel système on parle...
En p, je saurais répondre : Causale et Instable.

[polf]

Exhibe cette fonction et je te croirai.

Je sens que tu va chercher une solution en ajustant finement les conditions initiales.
Or pour la stabilité, ce n'est pas une solution mais toute solution. (autrement dit, CI nulle ou quelconque)

Pour le critère de stabilité:
- une fonction H est stable si toute entrée bornée donne une sortie bornée (ok)
- mais si H est instable, cela ne signifie pas nécessairement que toute sortie diverge. Si une seule diverge pour une entrée bornée, c'est suffisant pour que H est instable. (ie n'est pas toujours stable)

Comme tu le dis, je regarde si je trouve des couple (E,S) en exemple, mais ce n'est pas simple !

[polf]

Vous allez râler :

Si est la fonction échelon

e(t)= est non causal , borné, et a une sortie bornée !

[stefjm]

Ta question en #38 portait sur le circuit RC à résistance négative, je vais continuer dessus pour la présente réponse (c'est plus simple, et l'esprit est le même).
Remarque : je reprends la notation de Wolframalpha pour l'échelon unité, c'est à dire
Equation (1), EDO :



Equation (2), pour la réponse impulsionnelle :



Les deux fonctions suivantes sont solutions de l'équation (2) :





(Du coup, y'a une erreur de signe dans les messages #32 et #33 pour les RI en Laplace...)

=> une seule EDO, au moins 2 RI, au moins 2 systèmes...

Ok : Un système causal et un système acausal.
Je commence à comprendre la différence entre une approche de physicien et une approche d'automaticien.

Le physicien va préférer considérer que le système est stable (car sinon, il est malheureux avec la création d'énergie) et accepter l'acausalité.(La physique est T réversible) (C'est ce qui se passe peu ou prou pour le paradoxe de la force d'Abraham-Lorentz)

L'automaticien va préférer considérer que le système est causal (car sinon, il est malheureux pour le commander) et accepter l'instabilité (des systèmes qui partent en live, c'est courant...)

Je comprend enfin certaines incompréhension entre certains intervenants et moi. (b@z66, gatsu, coussin, guerom00, mariposa)

Question supplémentaire pour tout le monde : sachant que la TL (monolatérale) va de pair avec un système causal, et que la TF n'est pas convergente si la RI ne s'atténue pas en +/-inf, devinez quelle RI on va implicitement choisir en prenant soit la TF soit la TL ? A remettre en perspective avec #1 et la figure présentée.

Quasi Evident!
Merci pour la mise en perspective.

En fait, en Fourier, il y a en plus l'indétermination (i, -i) dont le carré fait 1.

1/(1+iw) : Instable Acausale
et
1/(1-iw) : Stable Causale

Il y a effectivement des gags de signes qui ont sans doutes une importance ici : Il va falloir se mettre d'accord.

Cordialement.

[stefjm]

Vous allez râler :

Si est la fonction échelon
e(t)= est non causal , borné, et a une sortie bornée !

Je n'ai pas compris le lien avec cette discussion.
e(t) est une fonction causale.
C'est la réponse de la soustraction d'un intégrateur et d'un intégrateur retardé.

[polf]

Une fonction causale est une fonction définie sur l'ensemble des réels dont le support est borné à gauche.

Une fonction non causale est définie au moins sur ]-oo ; a[.

est définie sur R

Donc : est définie sur R et est non causale.

La causalité ou non causalité n'implique pas de conditions sur la valeur que doit prendre la fonction.

[b@z66]

Bonjour,


C'est bien cela qui me dérange : tu ne vois pas le problème de ton raisonnement avec la bijectivité de la TF.

Tout d'abord, je tiens à m'excuser pour le te ton que j'ai employé surtout que tu avais bien dû faire la suite du raisonnement jusqu'au bout mais c'est ta mention de la bijectivité qui m'a posée problème puisqu'elle était fausse par rapport à ce que j'expliquais. Je la corrige donc(de même que le signe de la réponse impulsionnelle en Laplace).

avec

avec

Je n'ai jamais affirmé cela : merci de me citer pour prouver tes dires.
J'affirme que la TF directe de la RI d'un circuit RC instable n'est pas définie.

Je te dirais que tu as vrai si tu considères uniquement la réponse impulsionnelle issue de la transformée de Laplace inverse de la fonction de transfert. Seulement, je parlais uniquement, pour le coup, de l'utilisation de la transformée de Fourier inverse et, en l’occurrence, la réponse impulsionnelle e la transformée de Fourier inverse de la fonction de transfert existe bel et bien et est effectivement "anti-causale". Au passage, je ferais juste remarquer que cette causalité en automatique n'a pas grand chose à voir avec principale définition de la causalité en physique qui interdit juste les boucles temporelles(les voyages dans le passé), elle aurait en fait plus à voir avec la réversibilité temporelle des équations de la physique qui dit que lorsque l'on inverse l'axe du temps, les phénomènes physiques induits sont toujours plausibles "physiquement"(avec des inversions notables comme celle de divergence et de convergence temporelle ou donc encore de la stabilité et de l'instabilité).

Là, c'est insultant. Je te mets noir sur blanc le résultat du raisonnement en question (membre de droite de l'équation que je donne en #32), et non seulement tu passes à côté mais en plus tu affirmes que je n'ai pas su mener le raisonnement à terme.

Mea culpa à nouveau.

Diantre ! Les membres respectivement de droite et de gauche de mon équation en #32. Sauf que la manière dont j'ai écrit l'équation sous-entend que je prends directement la réponse temporelle du circuit RC instable, sans passer par la TL inverse (mais c'est pareil : le système est causal, on a le droit d'utiliser la TL monolatérale). Vois-tu donc ainsi que j'ai parfaitement compris ton raisonnement ?

Le problème vient toujours du fait que tu considères la seule RI "causale" comme unique alors que je t'ai montré le contraire.

Je comprends bien que tu considères que 1/(1-jw) et 1/(1-p) sont les mêmes fonctions de transfert, et que pour toi pouvoir interchanger sans aucune condition "p" et "jw" est un principe. Si tu restes sur ce principe, la discussion tournera en boucle : pas la peine de l'alimenter plus.

J'ai une formation d'électronicien à la base et j'ai appris qu'on pouvait déterminer la fonction de transfert d'un circuit RC en faisant juste son analyse harmonique en complexe(Zr=-R, Zc=1/jCw) et sans même passer par Laplace(ou alors sans s'en rendre compte). La fonction de transfert obtenue par ce raisonnement est bien 1/(1-jw) avec RC=1. Je me contente de suivre la procédure logique que j'ai apprise. Pour en revenir à un cadre plus général, celui de la transformée de Laplace bilatérale, on se rend compte qu'il existe différentes réponses impulsionnelles donnant la même expression de fonction de transfert(les domaines de convergences changent malgré tout comme indiqué dans le lien wiki sur la TL bilatérale). Je n'ai donné que deux réponses impulsionnelles correspondant à la TL-1 et à la TF-1 mais, de part la linéarité du système, toutes combinaisons linéaires pondérées des deux précédentes peut elle aussi être considérée comme une réponse impulsionnelle possible(avec bien sûr un autre domaine de convergence pour la TL bilatérale).

[b@z66]

Ce n'est en effet pas l'utilisation de Laplace ou de Fourier qui donne la zone de convergence de l'intégrale, mais bien la RI du système + le calcul mathématique. Tu ne peux pas poser p = jω alors que pour Re(p)=0 l'intégrale définissant la TL ne converge pas : si l'axe de imaginaires purs n'est pas dans la ROC de la TL, la RI du système n'admet pas de TF. C'est une autre formulation de ce que tu as déjà écrit par ailleurs (tu avais écrit "la RI doit s'atténuer en +/-inf", il me semble).

Je ne vois pas les choses comme ça. Je pense que c'est la zone particulière de convergence considérée qui limite de fait, au contraire, l'utilisation des signaux appliqués et observés respectivement en entrée et en sortie à des familles particulières(signaux "causaux" ou "anti-causaux", signaux divergents ou convergents,...)

[b@z66]

Je ne comprends rien à ce que tu dis là...
La réponse impulsionnelle d'un système n'est plus unique? J'en apprend un peu chaque jour.
delta(t) en entrée donne ri(t) en sortie.
Je ne vois pas pourquoi la ri(t) devrait dépendre des TF ou TL utilisée parce que les projections fréquentielles des signaux sont plus facile à manipuler que les projections temporelles.

D'un point de vue mathématique et dans le cadre générale de la transformée de Laplace bilatérale, la RI n'est effectivement pas unique. C'est la restriction que l'on s'impose à n'utiliser que des cas particuliers comme la TL ou la TF qui rend la RI unique. On avait déjà eu cette discussion, me semble t-il.

[stefjm]

Une fonction causale est une fonction définie sur l'ensemble des réels dont le support est borné à gauche.

Je n'ai pas cela comme définition!
Causale : fonction nulle pour les temps négatifs.

[stefjm]

D'un point de vue mathématique et dans le cadre générale de la transformée de Laplace bilatérale, la RI n'est effectivement pas unique. C'est la restriction que l'on s'impose à n'utiliser que des cas particuliers comme la TL ou la TF qui rend la RI unique. On avait déjà eu cette discussion, me semble t-il.

Oui. Et le critère EBSB pour toutes les entrées possibles permet de choisir la bonne RI

[b@z66]

J'ai essayé une résolution temporelle un peu différente de celle que j'avais faite.

Comme H peut s'écrire H=1/((p-p0).(p-p1).(p-p2).(p-p3).(p-p4))
pi pôles pouvant être comlexes

et que : e^(a.t) C 1/(p-a) C est la TL

Alors, en prenant soin de bien déterminer les bornes, on a :

s(t) = e^(p0.t) * e^(p1.t) * e^(p2.t) * e^(p3.t) * e^(p4.t) * e(t) où * est le produit de convolution

Je choisis e(t) = cos(w.t+phi)

Mais les calculs deviennent vite énormes....

Ce calcul ne sert à rien pour démontrer ou non la stabilité du système(je te l'ai déjà expliqué dans un précédent commentaire). Le fait que tu appliques un signal sinusoïdal à l'entrée d'un système linéaire va faire que tu vas obtenir en sortie de ce système(et ce sans même faire de calcul)...un signal sinusoïdal. C'est LA propriété fondamentale des systèmes linéaires qui explique que l'on se serve des fonctions de transfert. Le signal que tu doit appliquer en entrée pour étudier la stabilité doit directement être un dirac(qui permet de reconstituer n'importe quel signal d'entrée théorique par convolution).