Causalité / instabilité du système défini par H(ω)=1/(1+(jω)^5)

[phuphus]

Bonjour,

à l'occasion du fil Déphasage en physique, stefjm a proposé deux fonctions de transfert avec une question associée sur le déphasage.
La première fonction de transfert a été définie comme suit :



Si l'on remet en perspective cette fonction de transfert avec la discussion "Causalité et instabilité", on peut se poser la question du caractère causal ou stable de . J'ai mis les éléments de réponse que j'estimais contradictoires ici :
Causalité et instabilité

Mais il y a aussi de nombreux éléments de réponse sur les fils suivants (j'ai même peut-être manqué, dans ces discussions, la réponse que je cherche via ce sondage, allez savoir ) :
Causalité et instabilité
Déphasage en physique
Transformée laplace-fourier: interpretation (indigeste...)

Notez que j'ai un avis sur la question, mais que des zones d'ombre subsistent (c'est ma principale motivation quant au présent message). Je participerai donc au sondage comme tout le monde.

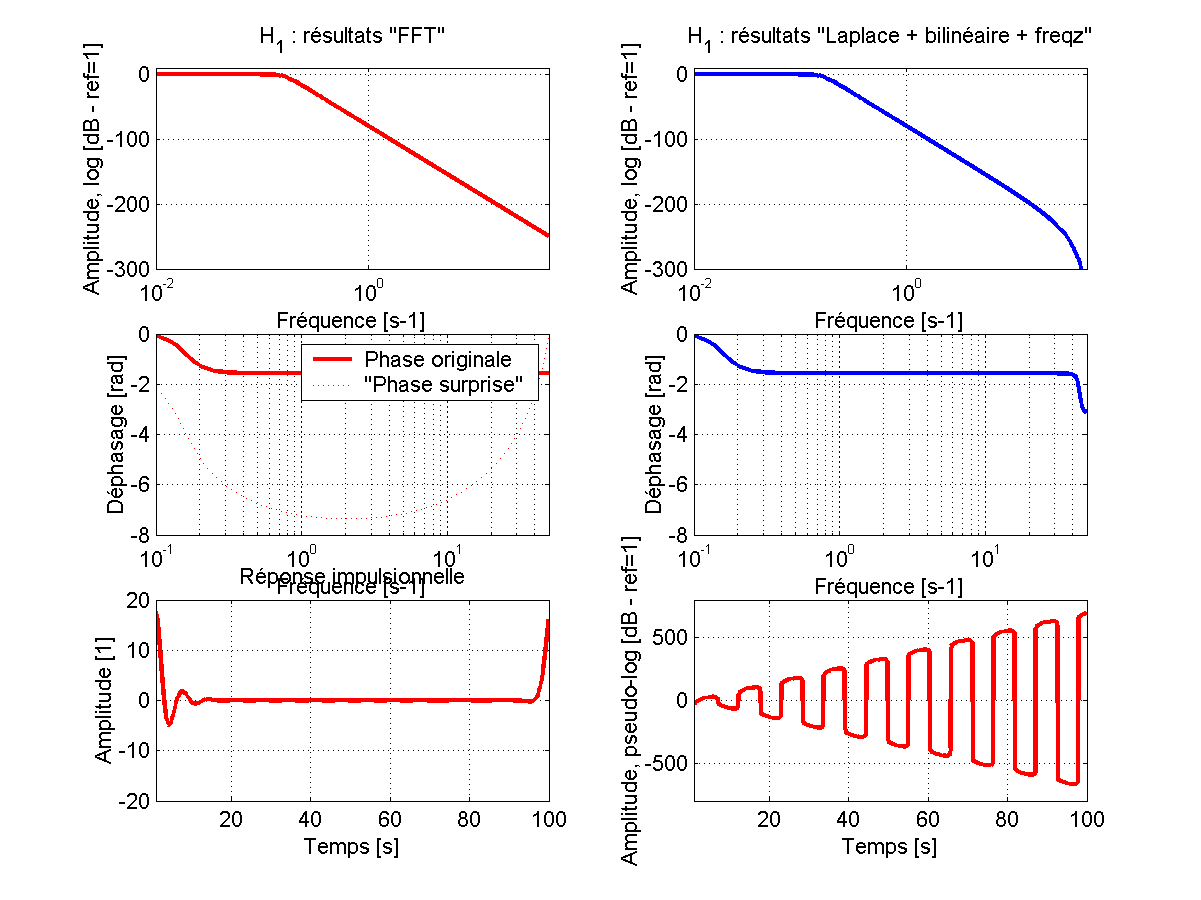
Je mets en pièce jointe une synthèse de résultats obtenus via Matlab concernant cette fonction de transfert. Les figures sont les suivantes :

Etude "FFT" : figures de gauche (courbes rouges)
- En haut : réponse en fréquence, niveau en dB
- Au milieu : réponse en fréquence, phase déroulée. En pointillés : "phase surprise". Trouver à quoi cela correspond vaut au plus un café.
- En bas : réponse impulsionnelle obtenue par FFT inverse

Etude "Laplace" : figures de droite (courbes bleues)
- En haut : réponse en fréquence, niveau en dB. Cette courbe est obtenue grâce à la fonction Matlab "freqz" appliquée aux coefs du filtre IIR obtenu par transformation bilinéaire
- Au milieu : réponse en fréquence, phase déroulée
- En bas : réponse impulsionnelle (filtrage d'un Dirac avec les coef du filtre IIR obtenu par transformation bilinéaire). Notez que l'amplitude absolue est en échelle log, et qu'au bout du temps de simulation on termine tout de même à 800 dB



Le code Matlab est le suivant (y'a un spoiler dans le code à propos du calcul de la phase surprise ; essayez de jouer le jeu !) :

% http://forums.futura-sciences.com/physique/669174-dephasage-physique.html
% FT de stefjm n°1
% FT_1 = 1/(1+(jw^5))
% Poles :
%  1+p^5 = 0
%  => les poles sont les racines cinquièmes de 1

close all ;
clear all ;
clc ;

% Constantes
  Fech    = 100                      ;
  Duree   = 100                      ;
  t       = [0:1/Fech:Duree-1/Fech]  ;
  Taille  = size(t,2)                ;
  freq    = [0:1/Duree:Fech-1/Duree] ;

% Formel
  syms p w
  FT = 1/(1-p^1) ;
  fct_laplace = simplify(expand(ilaplace(FT)))
  FT = 1/(1-(j*w)^1) ;
  fct_fourier = simplify(expand(ifourier(FT)))

% Calculs
  % P          = [1 exp(2*j*pi/5) exp(4*j*pi/5) exp(-2*j*pi/5) exp(-4*j*pi/5)] ;
  % Z          = 0 ;
  % K          = 1 ;
  % [Zd Pd Kd] = bilinear(Z,P,K,Fech) ;
  [B A]      = bilinear([1],[1 0 0 0 0 1],Fech) ;
  [H W]      = freqz(B,A,Taille/2)              ;

% RI par transformation bilinéaire
  signal    = zeros(Taille,1)'   ;
  signal(1) = Fech               ;
  RI_bilin  = filter(B,A,signal) ;

% RI par FFT inverse
  FT                 = 1./(1+(j*2*pi*freq).^5)      ;
  Nfft               = size(freq,2)                 ;
  Nyquist            = round(Nfft/2)                ;
  FT(Nyquist+2:Nfft) = conj(FT(Nyquist:-1:2))       ;
  RI_fft             = 0.5*real(ifft(FT))*(Nfft)    ;
  FT_fft             = fft(RI_fft) / (Nfft/2)       ;

% Détermination de la "phase surprise"
 Cliquez pour afficher
  Phi_surpr          = -imag(Hilbert(log(abs(FT))))        ;
  FT_Phi_surpr       = abs(FT) .* exp(j*Phi_surpr)         ;
  RI_Phi_surpr       = 0.5*real(ifft(FT_Phi_surpr))*(Nfft) ;
  FT_Phi_surpr       = fft(RI_Phi_surpr) / (Nfft/2)        ;

% Génération signal de base
  f                      = 4                                                   ;
  Debut                  = 1                                                   ;
  Nb                     = 5                                                   ;
  I_debut                = round(Debut * Fech + 1)                             ;
  I_fin                  = round(I_debut + Nb*Fech/f - 1)                      ;
  entree                 = sin(2*pi*f*t)                                       ;
  entree(1:I_debut-1)    = 0                                                   ;
  entree(I_fin+1:Taille) = 0                                                   ;
  entree(I_debut:I_fin)  = entree(I_debut:I_fin) .* bartlett(I_fin-I_debut+1)' ;

% Filtrage
  sortie_bilin             = filter (B,A         ,entree) ;
  sortie_RI_fft            = fftfilt(RI_fft      ,entree) ;
  sortie_RI_Phi_surpr      = fftfilt(RI_Phi_surpr,entree) ;

% Tracés
  freq         = freq(1:Nyquist)         ;
  W            = W*Fech/(2*pi)           ;
  FT_fft       = FT_fft(1:Nyquist)       ;
  FT_Phi_surpr = FT_Phi_surpr(1:Nyquist) ;

  %------------------------------------------------------------
  figure(1)
  
  subplot         (3,2,1)                                ;
  semilogx(freq,20*log10(abs(FT_fft)),'r','LineWidth',2) ;
  grid            on                                     ;
  axis            ([0.01 round(Fech/2) -300 10])         ;
  xlabel          ('Fréquence [s-1]')                    ;
  ylabel          ('Amplitude, log [dB - ref=1]')        ;
  title           ('H_1 : résultats "FFT"')              ;
  
  subplot         (3,2,3)                                ;
  semilogx(freq,unwrap(angle(FT_fft)),'r','LineWidth',2) ; hold on ;
  semilogx(freq,unwrap(angle(FT_Phi_surpr)),'r:')        ;
  grid            on                                     ;
  axis            ([0.1 round(Fech/2) -8 0])             ;
  legend          ('Phase originale','"Phase surprise"') ;
  xlabel          ('Fréquence [s-1]')                    ;
  ylabel          ('Déphasage [rad]')                    ;
  
  subplot         (3,2,5)                                ;
  plot(t,RI_fft,'r','LineWidth',2)                       ;
  grid            on                                     ;
  axis            ([1 Duree -20 20])                     ;
  xlabel          ('Temps [s]')                          ;
  ylabel          ('Amplitude [1]')                      ;
  title           ('Réponse impulsionnelle')             ;
  
  subplot         (3,2,2)                                ;
  semilogx(W,20*log10(abs(H)),'b','LineWidth',2)         ;
  grid            on                                     ;
  axis            ([0.01 round(Fech/2) -300 10])         ;
  xlabel          ('Fréquence [s-1]')                    ;
  ylabel          ('Amplitude, log [dB - ref=1]')        ;
  title           ('H_1 : résultats "Laplace + bilinéaire + freqz"')  ;
  
  subplot         (3,2,4)                                ;
  semilogx(W,unwrap(angle(H)),'b','LineWidth',2)         ;
  grid            on                                     ;
  axis            ([0.1 round(Fech/2) -8 0])             ;
  xlabel          ('Fréquence [s-1]')                    ;
  ylabel          ('Déphasage [rad]')                    ;
  
  subplot         (3,2,6)                                ;
  plot(t,20*log10(abs(RI_bilin)).*sign(RI_bilin),'r','LineWidth',2) ;
  grid            on                                     ;
  axis            ([1 Duree -800 800])                   ;
  xlabel          ('Temps [s]')                          ;
  ylabel          ('Amplitude, pseudo-log [dB - ref=1]') ;

-----

[phuphus]

Nouvelle figure, la précédente possède des échelles de fréquence différentes entre niveau et déphasage ; ça sera plus clair comme ça :
Figures_pour_sondage.png

[polf]

Bonjour,

La transformation de Laplace est la généralisation de la transformée de Fourier en fréquence ET ampitude. Sont intérêt est essentiellement théorique, il est rare d'utiliser en pratique p réel, ou non imaginaire pur, et donc on se reporte généralement sur Fourier pour l'aspect pratique.

Si l'on ne considère que l'aspect périodique (ou fréquentiel), alors F(p) = F(j.w) w->oméga

H(j.w)=1/(1+(j.w)^5) a 5 pôles de partie imaginaire proches de 1.

Compte tenu de l'équation source, il ne peut pas y avoir une seconde "cassure" de la pente, la pente est de 100 dB / décade.
Ce sont les courbes de la colonne de gauche qui sont justes.

[polf]

Concernant la stabilité d'une fonction dont la réponse est H(w), il faut se reporter à Nyquist :
http://fr.wikipedia.org/wiki/Diagramme_de_Nyquist

Concernant la causalité, la question est mal posée. La fonction f n'est pas causale ou non causale parce qu'elle à une transformée de Fourier ou de Laplace.

Une transformée de fourier n'est réelle que si elle est paire, donc non causale.

Il n'y a pas de transformée de Fourier réelle causale.

Tout ce que l'on peut dire est que pour une fonction non causale, son expression causale a la même transformée de Laplace que la transformée de Laplace de la fonction non causale. (t>=0)

Enfin, pour comparer des transformées de Fourier et de Laplace, il faut remplir les conditions de Fourier donc il faut une fonction non causale.

[A voir en vidéo sur Futura]

[b@z66]

Je pense que, d'un point de vue système, cela correspond à un procédé instable car avec des pôles dans le plan complexe tous situés sur le cercle unité mais avec des décalages d'angle de 2PI/5. On obtient donc nécessairement des pôles dans chaque demi-plan, donc à la fois des pôles stables et des pôles instables. Comme le comportement des pôles instables finit par prédominer en l'absence de signal d'entrée(le bruit suffit à faire diverger), le système est instable. Après pour ce qui est de la causalité, comme polf l'a indiqué, la solution n'est pas unique puisqu'on peut trouver comme réponse impulsionnelle correspondant à cette fonction de transfert un signal instable et causal en utilisant la TL⁻¹(on ne peut pas trouver de signal anti-causal en faisant une TL⁻¹!) et aussi un signal "stable" et "acausal" pour la TF⁻¹(c'est à dire non nul pour tout t).

[phuphus]

Bonsoir,

Si l'on ne considère que l'aspect périodique (ou fréquentiel), alors F(p) = F(j.w) w->oméga

C'est l'esprit de ce fil, mais je poserais le problème autrement.

 Cliquez pour afficher

p = jω ?
jω = p ?

Compte tenu de l'équation source, il ne peut pas y avoir une seconde "cassure" de la pente, la pente est de 100 dB / décade.
Ce sont les courbes de la colonne de gauche qui sont justes.

La cassure en HF doit plus être due à des problèmes numériques qu'à une réelle représentativité : il ne faut pas s'occuper de cela pour juger les courbes. En changeant les paramètres du script, la cassure bouge en fréquence : problème numérique. De plus, cette cassure arrive à -200 dB, je trouve cela non significatif.
Pour ma part, ce n'est pas cela qui me choque sur cette réponse en fréquence mais plutôt le fait qu'elle soit au même niveau que celle en "FFT" malgré une RI divergente. La réponse se situe dans le code de la fonction "freqz" de Matlab, mais je ne m'y suis pas encore plongé. Cela fait partie des "zones d'ombre" dont je parle en première intervention. Rien de bien compliqué, il me faut juste un peu de temps pour m'y atteler, donc si quelqu'un connaît de base, ça m'arrangerait.

Concernant la stabilité d'une fonction dont la réponse est H(w), il faut se reporter à Nyquist :
http://fr.wikipedia.org/wiki/Diagramme_de_Nyquist

Je ne vois pas l'application du diagramme de Nyquist ici. En l'utilisant, quelle est ta conclusion sur la fonction proposée ?

Concernant la causalité, la question est mal posée. La fonction f n'est pas causale ou non causale parce qu'elle à une transformée de Fourier ou de Laplace.

Une transformée de fourier n'est réelle que si elle est paire, donc non causale.

Tout ce que l'on peut dire est que pour une fonction non causale, son expression causale a la même transformée de Laplace que la transformée de Laplace de la fonction non causale. (t>=0)

Je suppose que ton dernier "Laplace" doit être remplacé par "Fourier". Dans tous les cas, c'est faux, puisque :
- la transformée de Laplace d'une fonction causale a la même forme que sa transformé de Fourier
- la transformée de Fourier est bijective
- une fonction de départ non causale et sa version causale sont différentes

La question de la causalité est bien posée : je parle bien dans l'intitulé de la causalité du système (donc de sa RI). La transformée de Fourier n'est qu'un outil dans l'histoire.

Il n'y a pas de transformée de Fourier réelle causale.

Oui, mais cela ne veut pas dire qu'une fonction non causale a forcément une TF réelle.

[phuphus]

Bonsoir,

Je pense que, d'un point de vue système, cela correspond à un procédé instable car avec des pôles dans le plan complexe tous situés sur le cercle unité mais avec des décalages d'angle de 2PI/5. On obtient donc nécessairement des pôles dans chaque demi-plan, donc à la fois des pôles stables et des pôles instables. Comme le comportement des pôles instables finit par prédominer en l'absence de signal d'entrée(le bruit suffit à faire diverger), le système est instable. Après pour ce qui est de la causalité, comme polf l'a indiqué, la solution n'est pas unique puisqu'on peut trouver comme réponse impulsionnelle correspondant à cette fonction de transfert un signal instable et causal en utilisant la TL⁻¹(on ne peut pas trouver de signal anti-causal en faisant une TL⁻¹!) et aussi un signal "stable" et "acausal" pour la TF⁻¹(c'est à dire non nul pour tout t).

C'est exactement un des points de ce fil : quel outil ? TF ou TL ? (De ce point de vue, la réponse est dans la question, je veux juste connaître les bonnes pratiques de chacun, et surtout pourquoi : qu'est-ce qui fait que tu considères que aussi bien la TF et la TL sont valables ici ?).

Le système (linéaire, toussa, toussa) est unique et peut être totalement défini par sa RI. Le caractère de la RI est clair, et pour moi, si TF et TL ne donnent pas les mêmes résultats, c'est que :





ne sont pas issues de la même RI, donc ne représentent pas le même système.

Pour poser la question autrement, pourquoi as-tu utilisé les propriétés de la TF pour déterminer ce qui se passe avec R négative ici :
http://forums.futura-sciences.com/ph...-edo-3.html#33

[polf]

La cassure en HF doit plus être due à des problèmes numériques qu'à une réelle représentativité : il ne faut pas s'occuper de cela pour juger les courbes. En changeant les paramètres du script, la cassure bouge en fréquence : problème numérique. De plus, cette cassure arrive à -200 dB, je trouve cela non significatif.
Pour ma part, ce n'est pas cela qui me choque sur cette réponse en fréquence mais plutôt le fait qu'elle soit au même niveau que celle en "FFT" malgré une RI divergente. La réponse se situe dans le code de la fonction "freqz" de Matlab, mais je ne m'y suis pas encore plongé. Cela fait partie des "zones d'ombre" dont je parle en première intervention. Rien de bien compliqué, il me faut juste un peu de temps pour m'y atteler, donc si quelqu'un connaît de base, ça m'arrangerait.

Oui, bien sûr que la seconde courbe a une seconde cassure dûe aux simulations matlab. Repliement de spectre dû au filtre IIR ou autres, peu importe.
Dans ce cas de figure, et du moment où l'on sait facilement calculer |H(jw)| et phase(H(jw)), la bonne solution apparait facilement sans utiliser fft() ou autre fct de Matlab.

Je ne vois pas l'application du diagramme de Nyquist ici. En l'utilisant, quelle est ta conclusion sur la fonction proposée ?

C'est le diagramme de Nyquist qui te répondra sur la question de stabilité. Je verrai si j'ai le temps de faire ce calcul. Mais quel est ton niveau et ta connaissance, as tu eu des cours sur Laplace, Nyquist, le théorème de Cauchy ?

Je suppose que ton dernier "Laplace" doit être remplacé par "Fourier". Dans tous les cas, c'est faux, puisque :
- la transformée de Laplace d'une fonction causale a la même forme que sa transformé de Fourier
- la transformée de Fourier est bijective
- une fonction de départ non causale et sa version causale sont différentes

Je voulais bien dire Laplace. Je me suis peut-être mal exprimé. La TL intègre seulement sur t positif. Je voulais dire qu'une fct causale et non causale, de partie causale identique, ont la même TL.
Je susi d'accord avec les 3 points que tu cites, et ça n'est pas en contradiction avec ce que j'avais dit.

Oui, mais cela ne veut pas dire qu'une fonction non causale a forcément une TF réelle.

Je n'ai pas dit cela. J'ai dit qu'une fonction paire non causale a forcément une TF réelle.

[polf]

Pour H(j.w)=1/(1+(j.w)^5)
La fonction en boucle ouverte est : T=ABS(w)^5.e^(i.pi/2)

Le diagramme de Nyquist de T est une demi-droite (Oy), dont aucun point n'a d'abscisse négative.

H est donc stable.

[phuphus]

Bonsoir,

Oui, bien sûr que la seconde courbe a une seconde cassure dûe aux simulations matlab. Repliement de spectre dû au filtre IIR ou autres, peu importe.
Dans ce cas de figure, et du moment où l'on sait facilement calculer |H(jw)| et phase(H(jw)), la bonne solution apparait facilement sans utiliser fft() ou autre fct de Matlab.

Pas de repliement ici, je ne génère rien au dessus de Fs/2. Les modules et arguments de la fonction sont en effet calculables sans aucune FFT, puisque j'ai directement donné la fonction de transfert en ω.
Lorsque tu écris "la bonne solution apparaît...", tu parles de la solution à la question que je pose ? Donc ici, que te dises les amplitudes et phases tracées ? Pour moi, sans savoir ce qu'est la "phase surprise", point de salut.

C'est le diagramme de Nyquist qui te répondra sur la question de stabilité. Je verrai si j'ai le temps de faire ce calcul. Mais quel est ton niveau et ta connaissance, as tu eu des cours sur Laplace, Nyquist, le théorème de Cauchy ?

Des cours sur Laplace oui (y'a 20 ans, et à l'époque j'appliquais bêtement les tables de TL), mais pas sur Nyquist ou Cauchy. Mais tu peux y aller sans te soucier de mon niveau, si je suis largué je le dirai.

Je voulais bien dire Laplace. Je me suis peut-être mal exprimé. La TL intègre seulement sur t positif. Je voulais dire qu'une fct causale et non causale, de partie causale identique, ont la même TL.
Je susi d'accord avec les 3 points que tu cites, et ça n'est pas en contradiction avec ce que j'avais dit.

En effet, c'est clair maintenant (le sous-entendu étant que TL désigne la TL monolatérale, ce qui est implicite vu l'usage).

Je n'ai pas dit cela. J'ai dit qu'une fonction paire non causale a forcément une TF réelle.

Bien entendu ! Mais remis en perspective avec la fonction H que j'ai donnée, j'ai implicitement compris (surinterprétation, toutes mes excuses pour ceci) que la présence d'une partie imaginaire dans H en ferait la TF d'une fonction causale. Quelle était donc ta motivation en écrivant qu'une TF est réelle pour une fonction temporelle paire ? Petite précision :

Une transformée de fourier n'est réelle que si elle est paire, donc non causale.

Non pas paire, mais symétrique conjuguée. Donc paire si réelle.
(je comprends aussi implicitement que tu as voulu écrire "Une transformée de fourier n'est réelle que si elle correspond à une fonction temporelle paire". Est-ce bien le cas ?)

Pour H(j.w)=1/(1+(j.w)^5)
La fonction en boucle ouverte est : T=ABS(w)^5.e^(i.pi/2)

Le diagramme de Nyquist de T est une demi-droite (Oy), dont aucun point n'a d'abscisse négative.

H est donc stable.

Merci pour ce calcul. Tu prends "-1" pour le gain de retour, c'est ça ?

Je suis d'accord pour H stable. Pour répondre complètement à la question, il reste le caractère causal.

[b@z66]

Bonsoir,


C'est exactement un des points de ce fil : quel outil ? TF ou TL ? (De ce point de vue, la réponse est dans la question, je veux juste connaître les bonnes pratiques de chacun, et surtout pourquoi : qu'est-ce qui fait que tu considères que aussi bien la TF et la TL sont valables ici ?).

Le système (linéaire, toussa, toussa) est unique et peut être totalement défini par sa RI. Le caractère de la RI est clair, et pour moi, si TF et TL ne donnent pas les mêmes résultats, c'est que :





ne sont pas issues de la même RI, donc ne représentent pas le même système.

C'est pourtant bien le même système représenter dans les deux cas mais, pour le coup, la réponse impulsionnelle ne se révèle pas unique. La TF va imposer implicitement que cette réponse impulsionnelle s'amortissent en t égal + et - l'infini tandis que la TF impose, elle, implicitement que cette réponse impulsionnelle soit "causale"(nulle pour t négatif). Après pour ce qui est des bonnes pratiques, on utilise la TL⁻¹ pour obtenir un résultat un peu moins ésotérique que celui la TF⁻¹ dans le cas des systèmes instables. Et quand on utilise la TL⁻¹, on obtient donc nécessairement une réponse impulsionnelle causale(la TF ne s'applique qu'à eux!) et, dans ce cas précis, instable.

Pour poser la question autrement, pourquoi as-tu utilisé les propriétés de la TF pour déterminer ce qui se passe avec R négative ici :
http://forums.futura-sciences.com/ph...-edo-3.html#33

Car je trouve idiot de demander de caractériser un système comme "causal" ou non(la définition de la causalité en automatisme étant déjà assez simpliste comparée à la définition utilisée en physique) en utilisant simplement la TL.

[b@z66]

Pour H(j.w)=1/(1+(j.w)^5)
La fonction en boucle ouverte est : T=ABS(w)^5.e^(i.pi/2)

Le diagramme de Nyquist de T est une demi-droite (Oy), dont aucun point n'a d'abscisse négative.

H est donc stable.

Bon, je me rend compte maintenant que tu parles d'un système bouclé(ce qui n'apparaissait pas dans le texte de ta première questionje n'ai pas lu le code). Dans ce cas là, il faut utiliser critère de Nyquist si la fonction que tu donnes est celle du système en boucle ouverte avec l'étude graphique de la fonction de transfert et le nombre de fois qu'elle entoure le point -1 du plan complexe.

[b@z66]

Bon, je me rend compte maintenant que tu parles d'un système bouclé(ce qui n'apparaissait pas dans le texte de ta première questionje n'ai pas lu le code). Dans ce cas là, il faut utiliser critère de Nyquist si la fonction que tu donnes est celle du système en boucle ouverte avec l'étude graphique de la fonction de transfert et le nombre de fois qu'elle entoure le point -1 du plan complexe.

Ben non, toujours pas, c'était bien la fonction du système complet que tu avais donné, semble t-il. Il suffit de déterminer les pôles de ta fonction de transfert en résolvant 1+p⁵=0 et de voir si certains de ces pôles sont dans le demi-plan de droite. Je t'ai déjà indiqué que la réponse est oui donc le système est instable.

Les pôles sont: e(j(PI/5+ 2K.PI/5)) avec k variant de 0 à 4

[polf]

Peux tu donner une démonstration ?

[b@z66]

Peux tu donner une démonstration ?

Il y a juste à appliquer le critère de stabilité concernant les demis-plans où se trouvent les pôles(les pôles doivent tous être à partie réelle négative pour que le système soit stable). Pour la démonstration, tu as le lien qui suit même si fondamentalement ce critère repose d'abord sur le théorème des résidus.

http://asi.insa-rouen.fr/enseignemen.../stabilite.htm

Enfin, pour le calcul des pôles, il n'y a rien à faire. La solution de p⁵=-1 est immédiate quand on a un peu l'habitude du calcul complexe. Comme dit plus haut, les 5 pôles sont situés sur le cercle unité du plan complexe(module égal à 1) et leur argument est simplement séparés de celui des autres de 2.k..PI/5(k entier variant de 0 à 4). Tu peux très bien vérifier par toi-même qu'ils respectent tous p⁵=-1.

Rappel: les pôles sont: e(j(PI/5+ 2k.PI/5)) avec k entier variant de 0 à 4

[b@z66]

Je corrige une erreur dans une de mes précédentes interventions qui rendait mon commentaire incompréhensible.

C'est pourtant bien le même système représenté dans les deux cas mais, pour le coup, la réponse impulsionnelle ne se révèle juste pas unique. La TF va imposer implicitement que cette réponse impulsionnelle s'amortissent en t égal + et - l'infini tandis que la TL impose, elle, implicitement que cette réponse impulsionnelle soit "causale"(nulle pour t négatif). Après pour ce qui est des bonnes pratiques, on utilise la TL⁻¹ pour obtenir un résultat un peu moins ésotérique que celui la TF⁻¹ dans le cas des systèmes instables. Et quand on utilise la TL⁻¹, on obtient donc nécessairement une réponse impulsionnelle causale(la TL ne s'applique qu'à eux!) et, dans ce cas précis, instable.

[polf]

Merci b@z66 pour ton explication.

Je reviens sur Nyquist parce que j'étais allé un peu trop vite. C'est loin pour moi !

H(w)=1/(1+j.w^5)

H(w)=A(w)/(1+A(w).B(w))
où : A(w)=1 et B(w)=j.w^5
T(w) = A(w).B(w) = j.w^5 gain en boucle ouverte

T(w) est la droite verticale passant par 0. Elle ne tourne pas autour de (-1,0)


1+T(w) possède : 3 zéros de partie réelle positive Z=3
aucun pôle P=0


Compte tenu des propriétés de T(w), pour que H soit stable, il faudrait Z=0, or Z=3.
Donc autant pour moi, le système est bien instable, y compris à basses fréquences. (comme Z non nul, pas de zone de fréquences stable).

[polf]

Pfiouuu, en regardant les docs sur la définition des pôles de H, je n'ai pas trouvé quelque chose qui disait clairement si un pôle de partie réelle positive et de partie imaginaire non nulle est bien un pôle. A ma décharge, les docs sur Nyquist sont souvent succintes, floues, et j'en ai trouvé des erronnées !

Donc , pour en avoir le coeur net, j'ai fait le calcul en temporel de la réponse du filtre.

On a p.F(p) C f'(t)
p^5.F(p) C f(5)(t) dérivée cinquième ( C pout TLI )

le système devient :

s'''''(t)+s(t)=e(t)

Après calculs, si e(t) = A.COS(w.t+phi0)
alors : s(t) = A/SQRT(1+w^10).COS(w.t-phi+phi0)
avec COS(phi)=1/SQRT(1+w^10)

On voit bien que s(t) ne diverge absolument pas, et est bien définie pour toute fréquence, y compris 0.

J'en conclus que, pour les pôles de H, on ne prend en compte que les pôles réels positifs purs. Il n'y a dans ce cas ni pôle ni zéro, et la fonction est :
STABLE ! Pfiouuuuu


Promis, je change plus d'avis

[b@z66]

Pfiouuu, en regardant les docs sur la définition des pôles de H, je n'ai pas trouvé quelque chose qui disait clairement si un pôle de partie réelle positive et de partie imaginaire non nulle est bien un pôle. A ma décharge, les docs sur Nyquist sont souvent succintes, floues, et j'en ai trouvé des erronnées !

Donc , pour en avoir le coeur net, j'ai fait le calcul en temporel de la réponse du filtre.

On a p.F(p) C f'(t)
p^5.F(p) C f(5)(t) dérivée cinquième ( C pout TLI )

le système devient :

s'''''(t)+s(t)=e(t)

Après calculs, si e(t) = A.COS(w.t+phi0)
alors : s(t) = A/SQRT(1+w^10).COS(w.t-phi+phi0)
avec COS(phi)=1/SQRT(1+w^10)

On voit bien que s(t) ne diverge absolument pas, et est bien définie pour toute fréquence, y compris 0.

J'en conclus que, pour les pôles de H, on ne prend en compte que les pôles réels positifs purs. Il n'y a dans ce cas ni pôle ni zéro, et la fonction est :
STABLE ! Pfiouuuuu


Promis, je change plus d'avis

Il ne s'agit pas du critère de Nyquist que j'ai appliqué(qui s'applique uniquement au système bouclé) mais bien du critère beaucoup plus général sur la stabilité(utilisant les demi-plans où se positionnent les pôles). Le critère de Nyquist n'est qu'une manière indirecte de déterminer les données de ce critère général en se servant de la fonction de transfert en boucle ouverte. En ce servant de ce critère général, la réponse est claire(à moins d'une erreur grossière de ma part): le système est instable.

Enfin, ton dernier calcul ne prouve strictement rien du tout. Tu as juste déterminé, pour une entrée sinusoïdale donnée du système, le signal "d'équilibre" que tu as en sortie. Rien n'interdit en soit d'avoir un équilibre donné en sortie d'un système excité sinusoidalement en son entrée, qu'il soit stable ou instable. C'est d'ailleurs comme ça que s'interprète la fonction de transfert d'un système linéaire(qu'il soit stable ou instable): pour un signal sinusoïdal en entrée, la fonction de transfert permet de connaître le signal sinusoïdal que tu as en sorti(d'ailleurs, d'une certaine façon, ton calcul aurait été plus simple en te servant directement de la fonction de transfert, plutôt que de revenir à la résolution de l'équation différentielle). Tout ça pour dire que même s'il existe un équilibre en sortie du système correspondant à ton signal d'entrée, cela ne signifie pas pour autant que cet équilibre est stable. Tu as du normalement apprendre qu'il existe différents types d'équilibre(stable, instable, métastable) or ton calcul a juste servit à déterminer un état d'équilibre sans indiquer son véritable type.

[b@z66]

Rien n'empêche, en théorie, un système instable positionné parfaitement sur son point d'équilibre de rester indéfiniment en équilibre mais cela ne le rend pas pour autant stable: il suffit dans la pratique de la plus infime perturbation pour faire diverger ce système de sa position d'équilibre.

[phuphus]

Bonsoir,

C'est pourtant bien le même système représenté dans les deux cas mais, pour le coup, la réponse impulsionnelle ne se révèle juste pas unique.

Comment un même système (LTI) peut avoir plusieurs RI ?

Le système que j'ai défini ici ne possède qu'une seule RI, et si TF et TL donnent des résultats différents, c'est bien qu'elles ne correspondent pas au même système. Même si leurs expressions sont identiques.

C'est une des choses que je veux mettre en lumière via ce fil : le domaine de validité des deux outils, dont l'affranchissement est une des raisons des respectivement 10 pages et 36 pages de discussion des fils "Causalité et instabilité" et "Transformée laplace-fourier: interpretation". Je ne m'en suis rendu compte qu'en me (re)plongeant dans tout ceci à l'occasion des FT données par stefjm dans le fil "Déphasage en physique"

La TF va imposer implicitement que cette réponse impulsionnelle s'amortissent en t égal + et - l'infini tandis que la TL impose, elle, implicitement que cette réponse impulsionnelle soit "causale"(nulle pour t négatif)

Oui, je suis entièrement d'accord, mais "à l'envers" :
- lorsque l'on a un système instable, la TF n'a aucun objet puisqu'elle n'existe pas (l'intégrale ne converge pas). Donc : si je suis capable de définir une fonction en jω sans singularités, c'est que cette fonction correspond forcément à un système stable. Cela rejoint ce que polf écrivait plus haut : "du moment où l'on sait facilement calculer |H(jw)| et phase(H(jw)), la bonne solution apparait facilement sans utiliser fft() ou autre fct de Matlab.". Pas besoin non plus de critère quelconque : la TF existe, le système est stable.
- lorsque l'on a un système causal, on peut utiliser la TL (monolatérale) puisqu'on ne tronque pas d'éventuelles infos avant t=0.

Ici, je prends une même expression, en remplaçant impunément (et c'est là le point central de la question) jω par p. Or, si mon système n'est pas causal, je n'ai pas le droit d'utiliser une expression obtenue avec des infos à t<0 pour y balancer du "p".

De même, si j'ai un système instable, je n'ai pas le droit de remplacer p par jω car je me mets explicitement dans une zone où l'intégrale ne converge pas (hors "ROC").

Ici, on a :
- une expression pour en jω qui correspond clairement à une RI non causale => je n'ai pas le droit de poser jω = p, sauf à me situer dans le cadre d'une TL bilatérale
- une expression en p qui correspond clairement à un système instable => je n'ai pas le droit de poser p = jω

Une des (nombreuses) questions que je me pose à l'étude de cette fonction de transfert est : existe-t-il un critère de stabilité en TL bilatérale ?
Je n'ai trouvé que ceci en français, et rien en anglais :
http://www.montefiore.ulg.ac.be/systems/SYST002/ex7.pdf

La partie intéressante est :
"Un système LTI est BIBO stable ssi sa ROC contient l’axe imaginaire"
En clair, ssi on peut poser , donc transformer la TL bilatérale en TF.

Et si stefjm passe par là, je pourrai même lui donner une explication "physique" de tout cela.

Après pour ce qui est des bonnes pratiques, on utilise la TL⁻¹ pour obtenir un résultat un peu moins ésotérique que celui la TF⁻¹ dans le cas des systèmes instables. Et quand on utilise la TL⁻¹, on obtient donc nécessairement une réponse impulsionnelle causale(la TL ne s'applique qu'à eux!) et, dans ce cas précis, instable.

Nous sommes donc d'accord, le tout est d'appliquer correctement chaque outil. Ici, je joue sur l'ambiguïté que peut provoquer la manière dont je définis mon système, mais je l'ai bien défini à la base en jω, pas en p.

Car je trouve idiot de demander de caractériser un système comme "causal" ou non(la définition de la causalité en automatisme étant déjà assez simpliste comparée à la définition utilisée en physique) en utilisant simplement la TL.

A condition de pouvoir utiliser, dans ce cas, les propriétés de la TF, qui ne s'appliquent que si les TF manipulées existent ! Et la TF pour un réseau RC à résistance négative n'existe pas, tu ne peux donc pas passer de la TF du système à R positive à la TF à R négative en jouant sur lesdites propriétés : réfléchir en Fourier ne transformera pas un système instable en système non causal.

[phuphus]

Bonsoir,

Merci b@z66 pour ton explication.

Je reviens sur Nyquist parce que j'étais allé un peu trop vite. C'est loin pour moi !

H(w)=1/(1+j.w^5)

H(w)=A(w)/(1+A(w).B(w))
où : A(w)=1 et B(w)=j.w^5
T(w) = A(w).B(w) = j.w^5 gain en boucle ouverte

T(w) est la droite verticale passant par 0. Elle ne tourne pas autour de (-1,0)


1+T(w) possède : 3 zéros de partie réelle positive Z=3
aucun pôle P=0


Compte tenu des propriétés de T(w), pour que H soit stable, il faudrait Z=0, or Z=3.
Donc autant pour moi, le système est bien instable, y compris à basses fréquences. (comme Z non nul, pas de zone de fréquences stable).

Si j'ai bien compris le diagramme de Nyquist, il impose B(ω) unitaire, tu ne peux donc pas poser B(ω)=jω^5.

Pfiouuu, en regardant les docs sur la définition des pôles de H, je n'ai pas trouvé quelque chose qui disait clairement si un pôle de partie réelle positive et de partie imaginaire non nulle est bien un pôle. A ma décharge, les docs sur Nyquist sont souvent succintes, floues, et j'en ai trouvé des erronnées !

Donc , pour en avoir le coeur net, j'ai fait le calcul en temporel de la réponse du filtre.

On a p.F(p) C f'(t)
p^5.F(p) C f(5)(t) dérivée cinquième ( C pout TLI )

le système devient :

s'''''(t)+s(t)=e(t)

Après calculs, si e(t) = A.COS(w.t+phi0)
alors : s(t) = A/SQRT(1+w^10).COS(w.t-phi+phi0)
avec COS(phi)=1/SQRT(1+w^10)

On voit bien que s(t) ne diverge absolument pas, et est bien définie pour toute fréquence, y compris 0.

J'en conclus que, pour les pôles de H, on ne prend en compte que les pôles réels positifs purs. Il n'y a dans ce cas ni pôle ni zéro, et la fonction est :
STABLE ! Pfiouuuuu

Oui, un pôle complexe est bien un pôle, et c'est bien la partie réelle qui est importante pour la stabilité. Quand on a le lien avec la physique, ça devient évident, et côté maths ça l'est aussi (obligation de "calmer" la RI avec une exponentielle suffisamment "intense").

Pour Nyquist et le "nombre de tours autours du point (-1,0)", il faut bien en effet comptabiliser le nombre de pôles "avec leur ordre de multiplicité"
http://asi.insa-rouen.fr/enseignemen...ns/nyquist.htm

Juste, c'est quoi TLI ??

Merci pour le calcul de l'ED. Elle est valable en Fourier, par contre en Laplace il faudrait inclure s(0-), non ? (et comme le système n'est pas causal...).

Promis, je change plus d'avis

Cela prouve que la question n'est pas triviale !

[polf]

@ b@z66
J'ai effectivement trouvé d'autres critères de stabilité dont celui dont tu parles : ie le système est stable si et seulement si tous les pôles sont à partie réelle négative .

Mais il y a d'autres méthodes. Le critère graphique de Revers indique au contraire que le système est stable.

Ayant Développé l'ensemble des solutions "monochromatiques", dont toutes les solutions sont bornées, et dont tous les noeuds du circuit, même hors de e(t) et s(t) sont bornés, je dois bien dire que maintenant, il me faudrait un contre exemple, une fonction e(t) donnant une sortie divergente, pour être convaincu.
Mais je cherche aussi de mon côté.

[phuphus]

Bonsoir,

Il ne s'agit pas du critère de Nyquist que j'ai appliqué(qui s'applique uniquement au système bouclé) mais bien du critère beaucoup plus général sur la stabilité(utilisant les demi-plans où se positionnent les pôles). Le critère de Nyquist n'est qu'une manière indirecte de déterminer les données de ce critère général en se servant de la fonction de transfert en boucle ouverte. En ce servant de ce critère général, la réponse est claire(à moins d'une erreur grossière de ma part): le système est instable.

Ce critère n'est valable que si le système est causal. Et comme il ne l'est pas

Enfin, ton dernier calcul ne prouve strictement rien du tout. Tu as juste déterminé, pour une entrée sinusoïdale donnée du système, le signal "d'équilibre" que tu as en sortie. Rien n'interdit en soit d'avoir un équilibre donné en sortie d'un système excité sinusoidalement en son entrée, qu'il soit stable ou instable. C'est d'ailleurs comme ça que s'interprète la fonction de transfert d'un système linéaire(qu'il soit stable ou instable): pour un signal sinusoïdal en entrée, la fonction de transfert permet de connaître le signal sinusoïdal que tu as en sorti(d'ailleurs, d'une certaine façon, ton calcul aurait été plus simple en te servant directement de la fonction de transfert, plutôt que de revenir à la résolution de l'équation différentielle). Tout ça pour dire que même s'il existe un équilibre en sortie du système correspondant à ton signal d'entrée, cela ne signifie pas pour autant que cet équilibre est stable. Tu as du normalement apprendre qu'il existe différents types d'équilibre(stable, instable, métastable) or ton calcul a juste servit à déterminer un état d'équilibre sans indiquer son véritable type.

Cela rejoint ce que stefjm et toi aviez déjà souligné ici, en clair "EBSB" :
http://forums.futura-sciences.com/ph...lite-5.html#64

[polf]

@ phuphus :
Comme tu dis, la question n'est pas triviale, et on dirait même que tout n'est pas parfaitement clair pour les personnes qui publient les critères de stabilité. Je veux dire que tout n'est pas forcément expliqué avec une grande rigueur.

Ici, c'est A(w) qui vaut 1 et B(w) qui vaut j.w^5. Mais ça n'est pas lié à Nyquist, mais au gain en boucle ouverte T(w)=A(w).B(w).

La TLI, est la transformée de Laplace inverse.


Je te cite :"Oui, un pôle complexe est bien un pôle, et c'est bien la partie réelle qui est importante pour la stabilité." Tu piques ma curiosité là dessus, car c'est le nerf de la guerre. La partie imaginaire doit elle être nulle ou pas ? J'en ai conclu à mon dernier post que oui. Mais si tu peux apporter des éléments, c'est avec plaisir.

Enfin, si H était instable, j'aimerais au moins que l'on puisse mettre un contre exemple en évidence.

[b@z66]

Bonsoir,


Comment un même système (LTI) peut avoir plusieurs RI ?

Tout simplement parce que, comme indiqué précédemment, en faisant une TF inverse ou une TL inverse, on fait des hypothèses implicites(l'original d'une TF tend vers 0 pour pour t allant vers + ou - l'infini tandis que l'original d'une TL est nulle pour t négatif). Les deux hypothèses pouvant se contredire, comme deux conditions initiales contradictoires, les résultats de transformée inverse à partir d'une TL et d'une TF d'une même fonction de transfert peut donner des résultats différents en tant que réponse impulsionnelle.

Le système que j'ai défini ici ne possède qu'une seule RI, et si TF et TL donnent des résultats différents, c'est bien qu'elles ne correspondent pas au même système. Même si leurs expressions sont identiques.

Comme dit plus haut, les TL et TF font des hypothèses implicites différentes sur les signaux de départ, le résultat de leur transformée inverse d'une même fonction de transfert peut donc être différent.

[b@z66]

@ b@z66
J'ai effectivement trouvé d'autres critères de stabilité dont celui dont tu parles : ie le système est stable si et seulement si tous les pôles sont à partie réelle négative .

Mais il y a d'autres méthodes. Le critère graphique de Revers indique au contraire que le système est stable.
.

Le critère du revers(qui est une forme particulière du critère de Nyquist) sert, tout comme le critère de Nyquist, à déterminer indirectement le nombre de pôles à partie réelle positive car il s'agit bien de cette dernière observation qui permet fondamentalement de juger dans ce cas de la stabilité. Je me souviens avoir vu la démonstration du critère de Nyquist sur le site d'une grande école, malheureusement la page a depuis disparu. Il faudrait que je me remette dans le bain de ce critère pour juger vraiment tes observations.

[b@z66]

Le critère du revers(qui est une forme particulière du critère de Nyquist) sert, tout comme le critère de Nyquist, à déterminer indirectement le nombre de pôles à partie réelle positive car il s'agit bien de cette dernière observation qui permet fondamentalement de juger dans ce cas de la stabilité. Je me souviens avoir vu la démonstration du critère de Nyquist sur le site d'une grande école, malheureusement la page a depuis disparu. Il faudrait que je me remette dans le bain de ce critère pour juger vraiment tes observations.

http://forums.futura-sciences.com/ph...n-nyquist.html

[b@z66]

http://forums.futura-sciences.com/ph...n-nyquist.html

Bon, je viens de revoir le critère de Nyquist et je crois avoir trouvé ton problème. Le problème que tu rencontres vient du fait que le critère de Nyquist s'applique pour des fonctions de transfert telles qu'elles peuvent être représentées en coordonnées polaires, en n'oubliant de la représenter pour toutes les fréquences à la fois positives mais aussi négatives, par un contour fermé(diagramme de Nyquist). Ceci est le cas pour la plupart des fonctions de transfert usuelles qu'elles représentent des passe-bas, des passe-bandes ou des passe-hauts, cela est plus précisément assuré par le fait que FT(f=-l'infini) tend vers FT(f=+l'infini) et par aussi le fait que FT(f=0⁺) tend vers FT(f=0⁻). Cela permet, plus faire simple, de refermer la courbe sur elle-même. Or, dans ton cas, tu as pris exactement le genre de fonction de transfert en boucle ouverte qu'il ne faut pas prendre puisque lorsque tu détermines son diagramme de Nyquist, tu tombes sur.... une droite! Difficile de fermer la courbe sur elle-même dans ce contexte. Il s'agit en quelque sorte, dans l'exemple que tu as pris, d'un cas dégénéré où le critère de Nyquist est pour le coup impossible à appliquer.

[b@z66]

A condition de pouvoir utiliser, dans ce cas, les propriétés de la TF, qui ne s'appliquent que si les TF manipulées existent ! Et la TF pour un réseau RC à résistance négative n'existe pas, tu ne peux donc pas passer de la TF du système à R positive à la TF à R négative en jouant sur lesdites propriétés : réfléchir en Fourier ne transformera pas un système instable en système non causal.

Faux, je te le prouve en deux coups de cuillère à pot. La fonction de transfert d'un circuit RC du 1er ordre (à résistance positive) peut s'écrire FTstable(w)=1/(1+tau.jw), sa réponse impulsionnelle vaut 0 pour t négatif et (1/tau)e(-t/tau) pour t positif. Dans le cas d'un circuit RC à résistance négative, on considère donc que R change de signe et donc que la constante de temps tau change aussi de facto de signe. On peut résumer ça par la fonction de transfert de ce circuit RC à résistance négative qui s'écrit donc FTinstable(w)=1/(1-tau.jw) en tentant de garder la même valeur algébrique pour tau que dans l'expression de la première fonction de transfert citée. Tu devrais remarquer tout de suite que FTstable(f)=FTinstable(-f) or tu as, dans les tables de propriétés de la TF, une propriété qui dit que la transformée inverse de fourier de H(-f) est h(-t)(en considérant que H(f) est la transformée de Fourier de h(t)). J'ai fait le gros du raisonnement, je te laisse le conclure. Pour en revenir à quelque chose d'intéressant que tu as mentionné, le ROC(le domaine de convergence, j'imagine) d'une fonction de transfert d'un système n'a pas en soi à être limité d'une façon ou d'une autre du fait que l'on utilise soit Fourier, soit Laplace. La fonction de transfert caractérise fondamentalement une propriété intrinsèque à la dynamique d'un système or une propriété intrinsèque d'un système physique ne doit pas dépendre du fait que l'on utilise tel ou tel outil mathématique abstrait(TL ou TF).