Incompréhension géodésiques (relativité générale)

[invited4aa5653]

Bonjour, je m'intéresse en ce moment à la relativité générale et à ce que ça implique sur la compréhension de la gravitation et je bloque sur un point.

Ce que je comprends, c'est que la courbure de l'espace temps induite par la présence d'un corps d'une certaine masse courbe l'espace temps. Les objets arrivant en ligne droite vers le corps voient leur trajectoire modifiée par la courbure de l'espace temps (ils suivent des géodésiques).

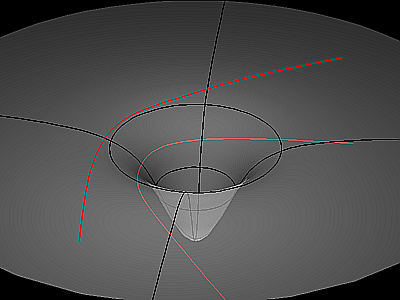
Cela correspond aux courbes rouges sur cette image :



Ce que je ne cerne pas, c'est le cas représenté par les lignes noires.

Wikipedia dit : "La première (en noir) correspond à un corps initialement au repos et qui tombe directement vers la source du champ de gravitation."

Autant je comprend parfaitement les lignes rouges car le corps possède déjà un mouvement qui est seulement dévié, autant je ne comprends pas par quelle magie un corps au repos peut acquérir un mouvement et tomber/chuter dans le puits alors qu'il est initialement au repos (action représentée par les lignes noires).

Question bonus : est il possible que ces deux interrogations soient liées et que l'univers entier soit bombardé comme une boule de bowling, ce qui expliquerait pourquoi nous sommes tous liés sur la même dimension du temps en constante évolution et ce qui expliquerait également la force "magique" qui définit le fait que le mouvement naturel d'un corps soit la chute libre ? (sur ce dernier point j'ai un doute, car dans le référentiel inertiel 'univers' aucune autre force externe ne devrait pouvoir s'appliquer.)

##j'ai scindé en deux discussions les deux questions distinctes pour éviter un éparpillement, mach3, pour la modération##
-----

[mach3]

Le sujet a déjà été abordé sur ce forum. Je manque de temps tout de suite, mais je vous retrouverai les fils de discussion pertinents (et on pourra approfondir certains points dans ce fil ci, si nécessaire). En attendant vous pouvez faire une recherche sur le forum.

m@ch3

[Resartus]

Wikipedia dit : "La première (en noir) correspond à un corps initialement au repos et qui tombe directement vers la source du champ de gravitation."

La phrase de wikipedia est pour le moins maladroite : le corps est plutôt momentanément au repos.

Imaginez tout bêtement un corps lancé à la verticale : au point le plus haut il est au repos et sa trajectoire dans l'espace après ce moment sera une demi droite.

Dans l'espace temps, c'est aussi une géodésique

[mach3]

Un premier fil à lire : https://forums.futura-sciences.com/p...t-gravite.html

m@ch3

[A voir en vidéo sur Futura]

[invite54165721]

@Avelan

Une géodésique est un ensemble de points, une variété de dimension 1. prenons le cas le plus simple d'un espace plat et une particule immobile dans un repere euclidien donné. A deux instants différents correspondront deux points différents de la géodésique (une droite). il y a une 4 tangente normée qui décrit son "mouvement" dans l'espace temps. pas besoin d'une chose mysterieuse pour la faire sortir de son immobilité supposée qui n'existe en fait pas.

[invited4aa5653]

Bonjour et merci pour vos réponses,

effectivement le sujet posé touche en plein coeur le point que j'ai du mal à cerner : on justifie la gravité par ... la gravité.

Une pomme passant à proximité de la terre verra sa trajectoire déviée par la courbure, c'est tout à fait logique. Mais qu'en est il de la pomme qui a déjà touché le sol ? Son mouvement devrait être stoppé par l'obstacle (le sol) pourtant elle est toujours en mouvement vers le centre de la terre puisqu'il suffit de la lancer en l'air pour qu'elle retombe ... quelle force l'attire puisque ce n'est pas la gravité qui n'en est pas une ?

J'avais plus ou moins compris que la pomme était en fait immobile, et que ce sont les objets qui se déplacent vers elle de manière à ce que la chute libre soit en fait un état immobile de la pomme et que c'est la terre qui se rapproche d'elle.

Quoi qu'il en soit je vais de ce pas lire le thread, et revenir vers vous avec mes questions quand j'aurais fini d'intégrer tout ça (ya du boulot )

[Deedee81]

Salut,

Une pomme passant à proximité de la terre verra sa trajectoire déviée par la courbure, c'est tout à fait logique. Mais qu'en est il de la pomme qui a déjà touché le sol ? Son mouvement devrait être stoppé par l'obstacle (le sol) pourtant elle est toujours en mouvement vers le centre de la terre puisqu'il suffit de la lancer en l'air pour qu'elle retombe ... quelle force l'attire puisque ce n'est pas la gravité qui n'en est pas une ?

Lorsque la pomme est sur le sol, son mouvement n'est plus géodésique/inertiel car elle subit une force la "réaction" du sol (le mot réaction est quelque peu inapproprié en RG, mais ça vient de Newton, c'est lui le spécialiste des pommes ). La même force qui fait mal au pied quand il y a une punaise sur le sol.

Parler d'immobilité de qui se rapproche ou bouge est quelque peu trompeur car.... ça dépend du référentiel choisi.
Dans un référentiel (non inertiel) attaché au sol, la pomme et le sol sont immobiles.
Dans un référentiel inertiel de chute libre le sol va vers le haut et la pomme aussi (poussée par la force de "réaction").

[mach3]

Une pomme passant à proximité de la terre verra sa trajectoire déviée par la courbure, c'est tout à fait logique. Mais qu'en est il de la pomme qui a déjà touché le sol ? Son mouvement devrait être stoppé par l'obstacle (le sol) pourtant elle est toujours en mouvement vers le centre de la terre puisqu'il suffit de la lancer en l'air pour qu'elle retombe ... quelle force l'attire puisque ce n'est pas la gravité qui n'en est pas une ?
[...]
Quoi qu'il en soit je vais de ce pas lire le thread, et revenir vers vous avec mes questions quand j'aurais fini d'intégrer tout ça (ya du boulot )

Les réponses sont dans le fil cité. Si la moindre chose n'est pas claire après avoir lu (et éventuellement relu, pas nécessairement tout, mais au moins les messages pertinents, en particulier ceux de Deedee et les miens (sans vouloir me faire de la pub...)), ne pas hésiter à demander ici.

m@ch3

[jacknicklaus]

Ce que je comprends, c'est que la courbure de l'espace temps induite par la présence d'un corps d'une certaine masse courbe l'espace temps. Les objets arrivant en ligne droite vers le corps voient leur trajectoire modifiée par la courbure de l'espace temps (ils suivent des géodésiques).

Oui, c'est çà, avec la condition importante que ces objets ne subissent aucune influence extérieure. Sinon, ils ne suivent plus une géodésique.

effectivement le sujet posé touche en plein coeur le point que j'ai du mal à cerner : on justifie la gravité par ... la gravité.

C'est la piège classique de cette représentation imagée. Il ne faut pas imaginer des objets pesants roulant sur une surface courbe. Ca c'est faux, et n'explique rien.

Il faut plutôt imaginer que cette vue concerne des trajectoires géodésiques en dimension 4. Dès lors, un objet réel 3D "immobile" dans un référentiel lié à la Terre par exemple comme source de gravitation, sans force extérieure, n'est pas immobile au sens 4D à cause de sa composante temps. Et le chemin direct de la ligne noire correspond à une géodésique 4D de l'objet, où celui ci n'est pas immobile (au sens 4D) à son point de départ : à ce point initial, il se déplace déjà dans sa géodésique 4D.

[Deedee81]

Salut,

En effet, il faut distinguer courbure extrinsèque et intrinsèque.
Dans une image comme celle-là, ce qu'on "voit" est avant tout la courbure extrinsèque alors qu'en RG ce qui compte est la courbure intrinsèque. Et la différence est loin d'être anecdotique.

Je viens de trouver cette petite explication assez simple et courte. A lire :
http://settheory.net/fr/courbure

[invited4aa5653]

Bonjour,

J'ai lu le fil (plusieurs fois oui ^^) et à défaut d'avoir tout compris, j'ai pu affiner ma question.

J'ai compris que le mouvement naturel des corps (chute libre) suivait une géodésique.

Ma question est : pourquoi est on en sans cesse en mouvement (tant qu'une autre force ne nous l'empêche pas) sur cette géodésique ? Quel est le 'moteur' qui nous fait nous déplacer sur cette géodésique ? la 4-accélération ?

[mach3]

Ma question est : pourquoi est on en sans cesse en mouvement (tant qu'une autre force ne nous l'empêche pas) sur cette géodésique ?

Pas sûr qu'il y ait une vraie réponse à la question, mais quelques éléments de réflexion :
Une ligne d'univers est une courbe paramétrée de l'espace-temps. On a une grande liberté de choix concernant le paramètre mais c'est forcément une fonction croissante monotone du temps propre le long de la ligne : en augmentant la valeur du paramètre, on parcourt la ligne du passé vers le futur (certains choix particuliers donnent une forme particulièrement simple aux équations, c'est le cas quand le paramètre est une fonction affine du temps propre le long de la géodésique, c'est à dire le temps propre, à un choix d'unité et d'origine près). A mesure que le temps propre d'un objet s'écoule, on doit passer d'évènement en évènement de sa ligne d'univers. Chaque évènement de la ligne d'univers d'un objet est une instance de l'objet à un instant différent de son existence.
Cela s'applique également à une géodésique qui n'est qu'un cas particulier de ligne d'univers : une ligne d'univers pour laquelle la 4-acceleration est strictement nulle (physiquement cela veut dire pas d'accélération ressentie pour l'objet dont c'est la ligne d'univers).

m@ch3

[invited4aa5653]

Je vois ..

Les géodésiques, l'accélération de la chute libre etc.. me paraissent très claires.

Ce qui ne l'est pas, c'est pourquoi si je dépose un corps (un satellite par exemple) à un endroit précis hors de l'attraction de la terre sans lui appliquer aucune force, celui-ci ne bougera pas et sera immobile (par rapport à la terre) alors que si je dépose un objet (une pomme) devant moi, celle-ci se mettra automatiquement à suivre un déplacement naturel le long de la géodésique (elle tombera en chute libre).

Pourquoi dans le cas de mon satellite ce dernier ne se déplace pas le long de la géodésique, il ne subit pas le mouvement naturel des corps qui est la chute libre, alors que ma pomme si.

La chute libre décrit la géodésique, ça je l'ai bien compris, mais qu'est ce qui motive un déplacement le long de cette même géodésique reste pour moi un mystère....

Le fait qu'il existe un "chemin le plus court" ne justifie pas un déplacement le long de ce dernier ...

[mach3]

pourquoi si je dépose un corps (un satellite par exemple) à un endroit précis hors de l'attraction de la terre sans lui appliquer aucune force, celui-ci ne bougera pas et sera immobile (par rapport à la terre) alors que si je dépose un objet (une pomme) devant moi, celle-ci se mettra automatiquement à suivre un déplacement naturel le long de la géodésique (elle tombera en chute libre).

Dans les deux cas la ligne d'univers est une geodesique. Loin de la Terre les geodesiques sont (presque) des droites de l'espace-temps et parmi elles il y en a qui sont parallèles à la ligne d'univers de la Terre. Quand deux lignes d'univers sont parallèles cela signifie physiquement que les objets correspondant sont immobiles l'un par rapport à l'autre. Près de la Terre, les geodesiques sont très courbées. Notamment, celles qui, en un événement, sont parallèles à la ligne d'univers de la Terre se rapprochent de celle-ci avant et après, tout comme une parabole d'équation y=x^2-1 est parallèle à l'axe des x quand x=0 mais s'en rapproche à gauche et à droite.

Pourquoi dans le cas de mon satellite ce dernier ne se déplace pas le long de la géodésique

Ben si, il se déplace aussi le long de la geodesique. Ou plutôt, les événements de la geodesiques sont les instances successives du satellite en des dates successives.

*mais qu'est ce qui motive un*déplacement*le long de cette même géodésique reste pour moi un mystère

L'écoulement du temps propre. Un événement sur une ligne d'univers (de genre temps, pour le genre nul c'est plus subtile) c'est l'instance d'un objet à une date donnée pour l'objet. L'instance de cet objet à une date ultérieure est en un autre événement de la ligne, situé plus loin vers le futur.

En relisant je crois que j'ai compris la question de travers on en reparle demain

m@ch3

[invited4aa5653]

Je pense que j'ai compris.

Si je résume :

* le satellite se déplace bien le long de sa géodésique. Il ne s'y déplace pas spatialement, mais temporellement. C'est imperceptible depuis la terre car sa géodésique n'est pas courbée et donc parallèle à celle de la terre.

* la pomme ne subit pas de force la déplaçant spatialement non plus. Cependant, la composante temps qui l'affecte induit un déplacement sur sa géodésique (comme le satellite). Celle-ci étant courbée, le déplacement temporel de la pomme induit une visibilité spatiale du phénomène : la chute libre. Effectivement, sans le temps, la pomme resterait en suspension devant nous.

* C'est donc le temps qui est moteur d'un déplacement le long des géodésiques, en tout cas pour un corps non affecté par d'autres forces.

[jacknicklaus]

* le satellite se déplace bien le long de sa géodésique. Il ne s'y déplace pas spatialement, mais temporellement.

non! Dans un référentiel lié à la Terre, le satellite se déplace spatialement, puisqu'il est en orbite à 400km/s par exemple pour l'iSS. C'est pas rien !

C'est imperceptible depuis la terre car sa géodésique n'est pas courbée et donc parallèle à celle de la terre.

euh... pour toi une orbite circulaire, c'est imperceptible et pas courbé ?? Ah bon ??

* la pomme ne subit pas de force la déplaçant spatialement non plus.

oui, en RG la gravité n'est pas une force

Cependant, la composante temps qui l'affecte induit un déplacement sur sa géodésique (comme le satellite).

oui, en gros. Mathématiquement, ce qui se passe c'est que l'équation de géodésique lie des déplacements spatiaux (qui sont nuls au départ, quand on vient tout juste de lâcher la pomme) et des déplacements temporels (qui eux ne sont pas nuls). Donc on peut en effet dire que lorsque le temps s'écoule, il faut nécessairement que le l'objet bouge spatialement, afin qu'il reste dans sa géodésique.

[Deedee81]

Salut,

euh... pour toi une orbite circulaire, c'est imperceptible et pas courbé ?? Ah bon ??

Petite précision, je ne sais pas si le problème vient de là (*), mais ça vaut la peine de le préciser :
(*) je ne crois pas car Avelan parlait de déplacement spatial, mais bon, la précision reste utile.

Pour un corps en orbite autour de la Terre :
- la trajectoire spatiale est un cercle (ou une ellipse) dont la courbure est loin d'être négligeable
- La trajectoire dans l'espace-temps est une spirale fortement étirée (à cause du fameux facteur c dans la métrique) et de très faible courbure (la gravité terrestre est relativement modeste et les effets relativistes tout autant, faut des trucs de haute précision comme les GPS pour devoir en tenir compte)

[invited4aa5653]

Salut, effectivement je parlais d'un satellite (objet conçu par l'homme) placé hors de l'attraction terrestre (du coup ce n'est plus un satellite au sens technique du terme), mon exemple porte énormément à confusion.

Remplaçons le 'satellite' de mon exemple par un objet aléatoire placé sans l'effet d'aucune force à un point libre de toute attraction, celui ci n'a donc pas de mouvement observable depuis le référentiel terrestre.

[Deedee81]

Salut, effectivement je parlais d'un satellite (objet conçu par l'homme) placé hors de l'attraction terrestre (du coup ce n'est plus un satellite au sens technique du terme), mon exemple porte énormément à confusion.

Il vaut mieux dire "sonde" alors.

Remplaçons le 'satellite' de mon exemple par un objet aléatoire placé sans l'effet d'aucune force à un point libre de toute attraction, celui ci n'a donc pas de mouvement observable depuis le référentiel terrestre.

Voir par exemple les "points de Lagrange". Par exemple, la sonde Gaïa est fixe par rapport à la Terre mais de l'autre côté du Soleil.

[jacknicklaus]

- la trajectoire spatiale est un cercle (ou une ellipse) dont la courbure est loin d'être négligeable
- La trajectoire dans l'espace-temps est une spirale fortement étirée (à cause du fameux facteur c dans la métrique) et de très faible courbure

En effet, il fallait préciser; On peut faire le calcul à la surface de la Terre, de mémoire on tombe sur c²/g soit un rayon de courbure proche d'une année lumière...

[invited4aa5653]

Il vaut mieux dire "sonde" alors.

Je retiens

Voir par exemple les "points de Lagrange". Par exemple, la sonde Gaïa est fixe par rapport à la Terre mais de l'autre côté du Soleil.

Déjà entendu parlé des points de Lagrange, je vais me renseigner ...

[invited4aa5653]

J'ai eu ma réponse sur le fil parallèle à celui-ci, mon problème était : En RG la chute libre est le mouvement naturel des corps soumis à aucune force (pas même la gravité). Comment un corps qui ne subit aucune force peut avoir un mouvement ?

J'ai compris grâce à cette intervention de Deedee81 (entre autre bien sûr !) :

Prenons par facilité un espace-temps plat. Disons deux dimensions spatiales horizontales et le temps représenté verticalement.
Sans force :
Un corps au repos (dans le référentiel "du sol") va suivre une géodésique qui est une ligne droite "verticale".
Un corps en mouvement va suivre une géodésique qui est une ligne oblique.
Et ce n'est que si l'on passe de l'un à l'autre qu'il faut fournir une force/impulsion, pour changer son état de mouvement.

Le corps est en mouvement même sans force extérieur car sa composante temps évolue. C'est l'évolution de la composante temps qui implique le mouvement du corps dans l'espace temps (le long des géodésiques) en l'absence de forces.

C'est d'ailleurs vérifiable facilement, si le temps s'arrête : la pomme ne tombera pas.

Merci pour votre patience

[Deedee81]

la pomme ne tombera pas.

La bosse sur la tête de Newton dit le contraire. Non, je rigole là
(de toute façon, c'est Gotlieb qui avait imaginé ça, en fait Newton avait VU la pomme tomber. Et encore, c'est pas lui qui l'a raconté mais un ami à lui dont le nom m'échappe)

Merci pour votre patience

On finit par y arriver.

[Benzki]

C'est d'ailleurs vérifiable facilement, si le temps s'arrête : la pomme ne tombera pas.

Bonjour. Et si on place la pomme dans un tunnel au centre de la terre ? En répondant à cette question, je pense que cela un très bon aboutissement de ce fil.

[invited4aa5653]

Bonjour. Et si on place la pomme dans un tunnel au centre de la terre ? En répondant à cette question, je pense que cela un très bon aboutissement de ce fil.

C'est une bonne question, je ne sais pas quelles formes prennent les géodésiques au centre de la terre.

[mach3]

C'est une bonne question, je ne sais pas quelles formes prennent les géodésiques au centre de la terre.

grosso-modo, tant que ça ne dépasse pas de la surface de la Terre (pomme lachée dans le tunnel à partir de l'altitude zéro, et on suppose qu'on a fait le vide dans le tuyau), le graphe r en fonction de t est une sinusoïde d'une période fixe (aux environ 2h je crois) indépendante de la profondeur à laquelle la pomme est lâchée. En fait les trajectoires correspondantes dans le cas général sont des ellipses dont le centre est le centre de la Terre et la période de rotation autour de ces ellipses est la même pour toutes les ellipses (bon en fait j'approxime en considérant que l'intérieur de la Terre est parfaitement homogène, mais ça donne une idée). Bien-sûr, aucune particule (sauf peut-être un neutrino qui par hasard serait incroyablement lent) ne parcourt ces géodésiques là : trop d'interactions (déjà dans l'atmosphère il y en a trop...).

m@ch3

[Benzki]

Bonjour Mach3 !

Oui, mais la question que j'avais soumise était non si on lache la pomme depuis une distance du centre, mais si on plaçait la pomme au centre. Plus de mouvement ! Ou alors on considère que la géodésique se referme sur elle-même, et donc l'objet fait une ellipse de rayon 0, et on peut considérer qu'il est toujours en mouvement bloqué sur lui-même. Juste ?

[mach3]

Ou alors on considère que la géodésique se referme sur elle-même

non.

La géodésique est simplement la même que celle du centre de la Terre. Dans le référentiel géocentrique, c'est une droite (et c'est la seule géodésique a être représentée par une droite dans ce référentiel).

m@ch3

[invited4aa5653]

La géodésique est simplement la même que celle du centre de la Terre. Dans le référentiel géocentrique, c'est une droite (et c'est la seule géodésique a être représentée par une droite dans ce référentiel).

Pourquoi ? La courbure doit être maximale au centre de la terre, j'aurais dit comme Benzki :

Ou alors on considère que la géodésique se referme sur elle-même, et donc l'objet fait une ellipse de rayon 0, et on peut considérer qu'il est toujours en mouvement bloqué sur lui-même

[mach3]

Pourquoi ? La courbure doit être maximale au centre de la terre

Peu importe la courbure, il y a toujours un repère où une géodésique donnée (voire même plusieurs) est représentée par une droite (de manière évidente il s'agit du référentiel où l'objet en mouvement géodésique est immobile).

m@ch3